week53 MAG

摘要

本周阅读了题为Failure Prediction for Large-scale Water Pipe Networks Using GNN and Temporal Failure Series的论文。这项工作开发了基于GNN的管网故障预测框架，整合管网特征、结构、地理及历史故障数据。创新构建图结构，优化GNN性能，引入时序故障学习模块。在双实际管网上验证效果卓越，辅助生成管道维护优先级，分析特征重要性，助力理解失效原因。框架可扩展至大规模基础设施网络，实现资产级故障预测。

Abstract

This week’s weekly newspaper decodes the paper entitled Failure Prediction for Large-scale Water Pipe Networks Using GNN and Temporal Failure Series. A GNN-based framework for pipeline network fault prediction integrates network features, structure, geography, and historical fault data. It innovatively constructs the graph structure, enhances GNN performance, and incorporates a temporal fault learning module. Proven successful in tests on two actual pipeline networks, it facilitates generating maintenance priorities, assesses feature importance, and aids experts in understanding the underlying causes of failures. This framework is scalable for use in large-scale infrastructure networks, enabling predictive maintenance at the asset level.

1. 题目

标题：Failure Prediction for Large-scale Water Pipe Networks Using GNN and Temporal Failure Series

作者：Shuming Liang; Zhidong Li; Bin Liang; Yu Ding; Yang Wang; Fang Chen

发布：CIKM2021 A会

链接：https://dl.acm.org/doi/10.1145/3459637.3481918

该文并未提供代码，因此下周将阅读https://arxiv.org/abs/2009.14332v5作为替代，大致信息如下

标题：Multi-hop Attention Graph Neural Network

作者：Guangtao Wang, Rex Ying, Jing Huang, Jure Leskovec

发布：IJCAI2021 A会

链接：https://arxiv.org/abs/2009.14332v5

代码链接：https://github.com/xjtuwgt/gnn-magna

2. Abstract

该文综合考虑管道的特性、网络结构、地理邻近效应和时间序列等因素，建立了管网失效预测框架，将多跳图神经网络(GNN)应用于故障预测。该文提出了一种构造地理图形结构的方法，该方法不仅依赖于物理连接，而且依赖于管道之间的地理距离。为了区分具有不同属性的管道，在每个GNN层的邻域聚合过程中采用了注意机制。此外，残差连接和分层聚合也被用于避免深度gnn中的过度平滑问题。以往故障表现出强烈的时间相关性。受此启发，开发了一个模块来学习管道的演化效应和历史故障对管道当前状态的影响（time-decayed excitement）。在两个真实的大型管网中对所提出的框架进行了评估。它优于现有的统计、机器学习和最先进的GNN基线。该框架为水务公司提供了核心数据驱动的主动维护支持，包括定期管道检查、管道更新计划和传感器系统部署。它可以在未来扩展到其他基础设施网络。

3. 预测标准

3.1 问题提出

形式上，给定一个带有二进制管道的管网，可以将管道表示为节点来构造图$\mathcal{G}(\mathcal{V},A,X)$，其中$\mathcal{V}$是节点的集合，相邻矩阵$A\in {\mathbb{R}}^{N\times N}$二进制中存储了行和列被节点索引的结构信息，a的第i行和第j列中的$a_{i,j}$表示节点i与j之间的连通性。如果节点的表达式i与j没有关联，则其值为0，否则为非0。特征矩阵$X\in {\mathbb{R}}^{N\times f}$表示节点的特征，其中X的第i行是节点的特征向量$x_i\in {\mathbb{R}}^f$。另外，将${\mathcal{H}}_i$表示为管道的历史失效事件集。将故障预测任务转换为一个二元分类问题，即管道是否会在未来的时间窗口内发生故障。因此，任务表述为学习一个模型 M : { G ( A , X ) , { H i } i = 1 N } → y ∈ R N \mathcal M:\{\mathcal G(A,X),\{\mathcal H_i\}^N_{i=1}\}\rightarrow y\in \mathbb R^N M:{G(A,X),{Hi​}i=1N​}→y∈RN，其中y的第i项是第i管道的估计失效风险。

3.2 数据预处理

地理图谱结构构建

管网在地理上呈大面积分布。无论管道是否物理连接，彼此靠近的管道往往表现出相似的失效趋势。在该项工作中，提出了一种不仅根据物理连接，而且根据管道之间的距离构建地理图结构的方法。在形式上，地理图形结构定义为：

Definition 4.1：地理图形结构。设地理图的结构用$A\in {\mathbb{R}}^{N\times N}$表示，它是具有N个节点的图的邻接矩阵。$a_{i,j}$位于矩阵A的第i行第j列且为非零值，若i节点和j节点邻接或$dist(i,j)<\rho$，$dist(\cdot )$表示节点i和j之间的距离。否则，$a_{i,j}=0$。

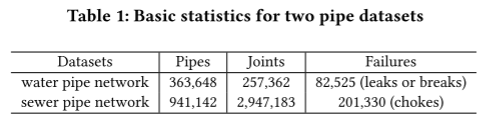
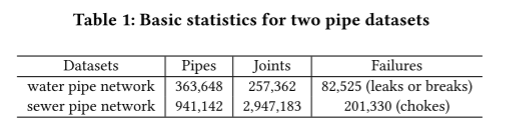
这项工作中使用数据集中每条管道的质心作为节点，构造未加权的地理图结构。如表1所示，构建的图中水管数据集节点数为363,648，下水管道数据集节点数为941,142。

特征工程

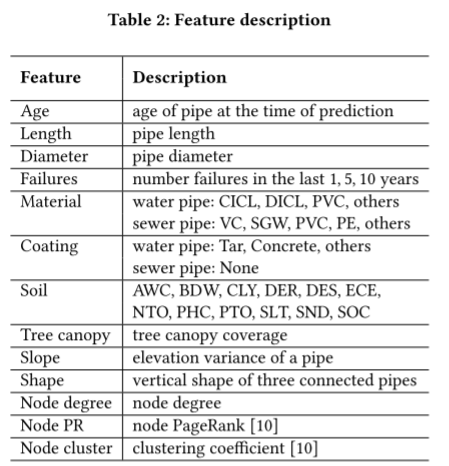
表2列出了特征及其描述。对于管道的基本属性，年龄、长度和直径是连续的特征。对于故障，分别计算过去1年、5年和10年每条管道的故障数量。管道材料和外部涂层材料(只有水管有)是分类特征。将很少使用的材料归类为“其他”，然后进行单热编码。

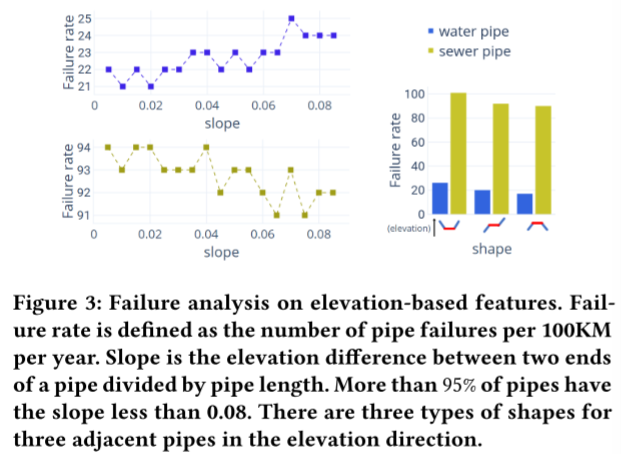
环境和物理条件是导致管道失效的重要因素。制作了12个土壤特征，表明水容量，密度，组成(粘土，淤泥，砂，有机碳)，有效阳离子交换，pH值等。众所周知，树根是管道失效的主要原因，因为树根更容易生长在管道周围，并从管道中吸收水分和养分。基于现有的树冠数据，使用树冠覆盖管道的百分比作为该管道的特征。该文还研究了基于高程数据设计的特征的失败率。两个基于高度的特征用于故障预测。如图3所示，其中一个特征是反映管道高程变化的坡度。另一种是中间管的三根相邻管的垂直形状。

此外，计算了节点度、PageRank和聚类系数三个节点级图结构属性。总的来说，水管和下水管道分别有31个和29个特征。

时间故障序列

对于管道，历史故障对其当前状态的影响表现出强烈的时间模式。在数据预处理中，如图1所示，将每个管道梗的失效记录提取成一个时间序列:
H i = { t 0 , . . . , t h , . . . } (1) \mathcal H_i=\{t_0,...,t_h,...\} \tag{1} Hi​={t0​,...,th​,...}(1)

3.3 模型架构MAG

大多数gnn遵循一种邻域信息聚合算法，通过聚合其邻居的表示并将结果与自身结合，逐层更新节点的表示。形式上，GNN的第l层中每个节点$v\in V$的表示为:
h v ( l ) = C O M B I N E ( l ) ( h v ( l − 1 ) , A G G ( l ) ( { h u l − 1 } u ∈ N ( v ) ) ) (2) h^{(l)}_v=COMBINE^{(l)}(h_v^{(l-1)},AGG^{(l)}(\{h^{l-1}_u\}_{u\in\mathcal N(v)})) \tag{2} hv(l)​=COMBINE(l)(hv(l−1)​,AGG(l)({hul−1​}u∈N(v)​))(2)

其中N(v)为节点v的邻居集合。

用节点v的特征向量$x_v$初始化$h_v(0)$。$COMBINE(\cdot )$和$AGG(\cdot )$是由特定的模型定义。GraphSAGE在$COMBINE(\cdot )$中进行串联，并基于LSTM架构或最大池化操作，提出了几种$AGG(\cdot )$函数。图卷积网络在聚合步骤中同时对节点𝑣及其邻居的状态进行平均。最近的一些研究使用注意机制来突出在$AGG(\cdot )$​中更相关的邻居信息，而不是平等地对待所有邻居。总结的方法$COMBINE(\cdot )$和$AGG(\cdot )$在表3中

在该框架中，实现了三种GNN技术，即多跳聚合、注意力机制、残差链接以及分类聚合

多跳聚合

在该框架中，遵循DEA-GNN中的多跳方法。将式2中的变量$AGG(\cdot )$变为:
A G G ( l ) ( { h ( l − 1 ) u } u ∈ N ( v ) ) → A G G ( l ) ( { h u ( l − 1 ) } S P D ( v , u ) < k ) (3) AGG^{(l)}(\{h^{(l-1)_u}\}_{u\in \mathcal N(v)})\rightarrow AGG^{(l)}(\{h^{(l-1)}_u\}_{SPD(v,u)<k})\tag{3} AGG(l)({h(l−1)u​}u∈N(v)​)→AGG(l)({hu(l−1)​}SPD(v,u)<k​)(3)
$SPD(\cdot ,\cdot )$计算两个节点之间的最短路径距离，k为超参。

一般情况下，设置k= 2或3就足够了，这样可以保证聚合集中在局部邻居信息上，避免来自高阶邻居的“噪声”信息。在实验中，k是通过权衡计算复杂性和性能来选择的。图1展示了多跳聚合，其中中心节点的2跳邻居的消息在一个GNN层中聚合。

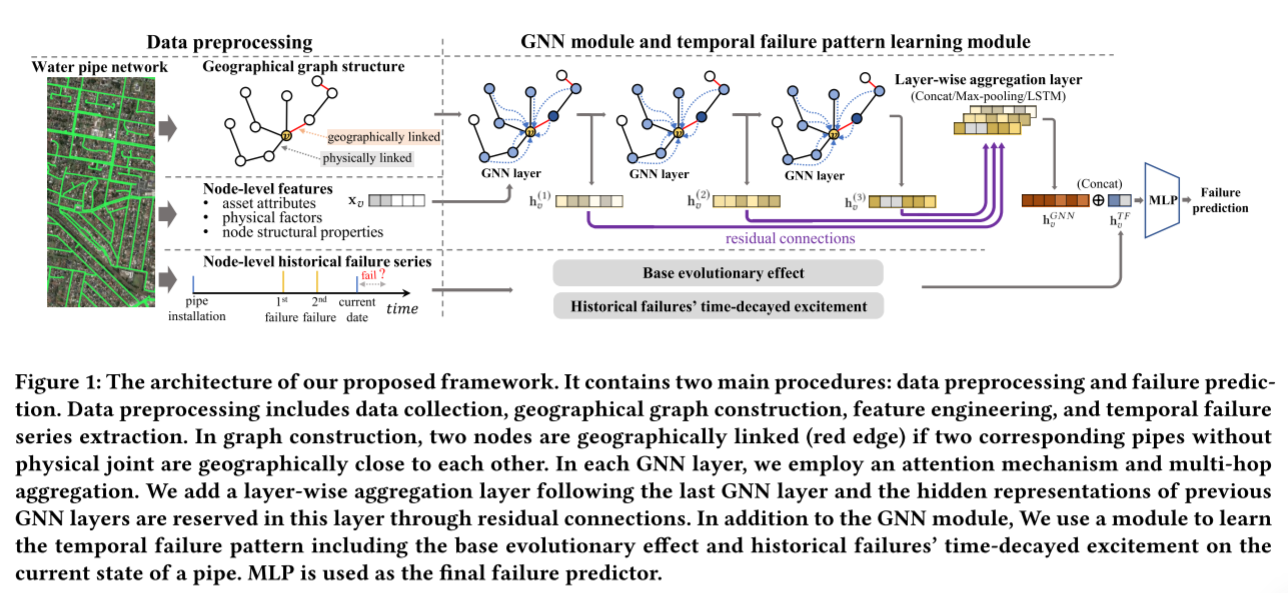
注意力GNN层

GNN层中的邻域聚集可能导致节点的偏差表示，特别是当相邻节点具有完全不同的属性时。采用注意力机制来解决这个问题。它允许模型学习两个相邻节点之间的自适应重要性权重，从而在聚合过程中通过突出相关程度高的节点的消息而抑制相关程度低的节点的贡献来区分相邻节点。

在这项工作中，采用了GAT提出的注意机制。形式上，中心目标节点v的邻居节点u的关注系数为:
$${\alpha }_{vu}^{(l)}=\frac{\text{exp}(\text{LeakyReLU}(a^{(l)}\cdot CONCAT(h_v^{(l-1)},h_u^{(l-1)})))}{{\sum }_{SPD(v,w)<k}\text{exp}(\text{LeakReLU}(a^{(l)}\cdot CONCAT(h_v^{(l-1)},h_w^{(l-1)})))}\text{\hspace{1em}(4)}$$
其中$a^{(l)}\in {\mathbb{R}}^{2d}$是可训练的第l层的权向量,$h_v^{(l-1)}\in {\mathbb{R}}^d$和$h_u^{(l-1)}\in {\mathbb{R}}^d$分别是节点v和u在第(l-1)层输出状态。$CONCAT(\cdot ,\cdot )$是连接操作。$LeakyReLU$​是一个激活函数。

对于GNN模块中Eq. 2中GNN层的最终表述，在第一GNN层中设置了联结(concatation)的变量为$CONBINE(\cdot )$，设置了平均池化(mean-pooling)的变量为$AGG(\cdot )$。结合Eq. 4中的注意机制，将第一GNN层给出的节点𝑣的输出表示形式化为:
$$\begin{gathered} h_v^{(l)}=\text{ReLU}(CONCAT(x_v,W^{(l)}\cdot \sum {\alpha }_{vu}^{(l)}{x}_u)) \\ \text{where}u:SPD(v,u)<k\text{\hspace{1em}(5)} \end{gathered}$$
由于在GNN模块中使用了残差连接和分层聚合，因此对于剩余的GNN层，不再需要连接操作。因此，将第l层（l>1）GNN层设为:
$$\begin{gathered} h_v^{(l)}=\text{ReLU}(W^{(l)}\cdot \sum {\alpha }_{vu}^{(l)}{h}_u^{l-1}) \\ \text{where}l>1;u:SPD(v,u)<koru=v\text{\hspace{1em}(6)} \end{gathered}$$

残差连接以及分层聚合

基于邻域聚合算法的常见gnn往往较浅，较深的gnn被证明存在过平滑和梯度退化。在GNN中堆叠越来越深的层可能会对来自太宽范围的邻居的信息进行过度平均，从而导致中心目标节点的有用信息可能被“洗掉”。

为了进一步增强框架的表达能力，该文采用了jkgnn的思想。如图1所示，在最后一个GNN层之后添加一层。这一层存储来自前GNN层的隐藏表示。换句话说，每个GNN层的输出都与该层有残差连接或跳变连接。在这一层对这些表示实现分层聚合。因此，GNN模块生成的节点𝑣的最终表示为
$$h_v^{GNN}=AGG([h_v^{(l)},...,h_v^{(l)}])\text{\hspace{1em}(7)}$$
如表3所示，对变量𝐺𝐺(·)采用了三种聚合方案，即concatation、max-pooling和LSTM-attention。concatation将这些表示组合在一起，而maxpooling应用$max(\cdot )$。这两种聚合方法都不是节点自适应的，也不引入与特定节点相关的附加参数。相比之下，LSTM-attention是节点自适应的，需要计算每个节点的注意分数。

3.4 时域故障模式识别

点过程

随机点过程已被证明是处理这类时序失效数据的有效工具。本质上，点过程的特征是条件强度函数$\lambda (t)$，其中，考虑到t之前的历史事件，其中$\lambda (t)dt$是在一个小窗口$[t,t+dt]$内发生事件的可能性。具体来说，Hawkes点过程的公式为

$$\lambda (t)={\lambda }_0(t)+\sum _{t_h\in \mathcal{H},t_h<t}\mathcal{K}(t-t_h)\text{\hspace{1em}(8)}$$

时域故障表示

为了捕获故障数据中的时间模式，该框架添加了一个受Hawkes过程启发的时间故障模式学习模块。形式上，该模块给出的节点v对时间失效效应的表示$h_v^{TF}$为:
$$\begin{gathered} h_v^T=\mu +(\omega +\mu )e^{-\delta t} \\ {h}_v^F=\sum _{t_h\in {\mathcal{H}}_v,t_h<t}\alpha e^{-\beta (t-t_h)} \\ {h}_v^{TF}=\text{ReLU}(CONCAT(h_v^T,h_v^F))\text{\hspace{1em}(9)} \end{gathered}$$
该框架称$h_v^T$为基础进化效应，它是仅与管道年龄相关的函数t，其中$\omega$是t=0时的初始失效风险，$\delta$是指数衰减率，并且$\mu$描述了回归水平。例如，随着年龄t的增加，当$\omega >\mu$时，$h_v^F$呈指数衰减，当$\omega <\mu$时指数增加。$h_v^F$称为历史故障的时间衰减激励，其中，$\alpha$时延为指数衰减函数的激励跳变大小。$h_v^F$是管道v所有历史故障对其时间t状态的激励效应的集合。

3.5 故障检测器

使用多层感知器(MLP)作为该框架的预测器。如图1所示，它将GNN输出和时间故障表示的串联起来，即$CONCAT(h_v^{GNN},h_v^{TF})$作为输入，并预测最终的故障风险。利用二元交叉熵损失对整个模型进行端到端优化。如果在给定的时间窗口内管道上发生了故障事件，则将该管道的目标赋值为1，否则为0。时间窗口根据下行任务设置。

4. 文献解读

4.1 Introduction

该文提出以往模型忽略了管网的两个关键信息，即管道连通性结构和地理邻近效应。根据行业惯例，如果一根管道发生故障，则由于水锤等物理效应，与该管道在同一路线上的管道(连接管道)会出现更多的故障。另一方面，由于这些管道暴露在类似的环境因素中，如土壤性质、地面振动等，即使与失效管道没有连接，也会在附近的管道上观察到更多的失效。

基于提高预测质量的动机，该文提出了一种基于图的机器学习框架MAG (Multi-hop Attention-based GNN)，采用图神经网络(Graph Neural Network, GNN)来学习管网中的特征、结构和地理相邻信息。gnn在许多应用中取得了巨大的成功。gnn的基本思想是在图结构上传播和聚合邻域信息。然而，将gnn应用于管网故障预测存在一些挑战。

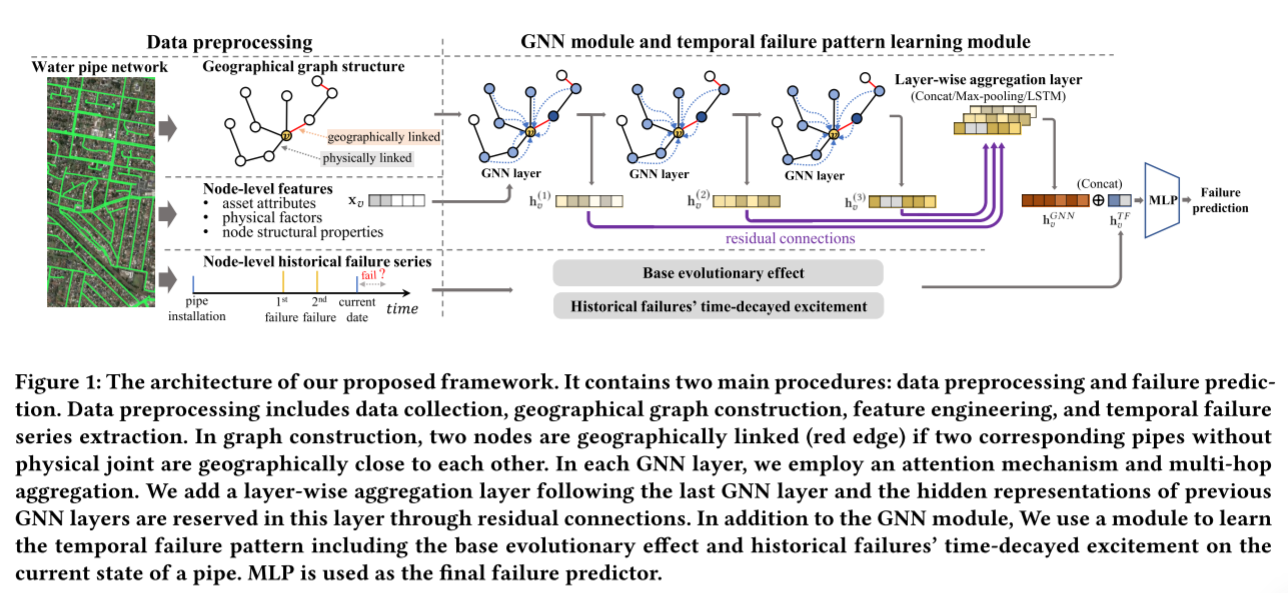
为了了解时间失效模式，开发了一个模块作为GNN模块的补充。受点过程的启发，该模块学习了两个独立的时间效应，如图1所示。一种是基于老化管道将更频繁地失效这一事实的基本老化效应。另一个是刺激效应，即一个失败会在短时间内引起更多的失败。

这项工作基于两个现实世界的大型管网。该文框架在这些数据集上进行了评估，实验结果表明，它优于统计和机器学习模型，以及最先进的GNN基线。所提出的框架嵌入到已实施的平台中，为主动维护提供重要的数据驱动支持，例如定期管道检查、管道更新计划和管道故障原因研究。该文还使用模型研究了特征的重要性，这有助于领域专家识别和理解导致管道失效的物理因素。

4.2 创新点

该文所提出的MAG能够解决这些挑战：

1. 基于管网构建一个图结构，该图结构应该连接GNN的结构和地理信息。在这项工作中，将管道表示为节点。当然，节点之间的边可以根据管道之间的物理连接来构造。另一方面，如果两个对应管道之间的地理距离在一定范围内，将两个节点视为邻接。
2. 将gnn的邻域信息聚合用于消除突发噪声。然而，这种聚集可能会导致管道故障预测的关键信息丢失，特别是当管网中连接的管道变化较大时。MAG将采用注意机制，根据相邻节点的相关性学习自适应的注意权重，从而在聚合过程中区分不相似的邻居。
3. 证明GNN存在过度平滑的问题，即深层GNN层中目标中心节点的表示可能会因平均来自太宽范围邻居的信息而过度平滑，从而导致目标节点的有用信息可能被覆盖。为了克服这一问题，将包括残差连接和分层聚合在内的GNN技术应用于MAG，通过保留每个隐藏GNN层的潜在表示以用于最终预测，从而防止过度平滑学习。

4.3 实验过程

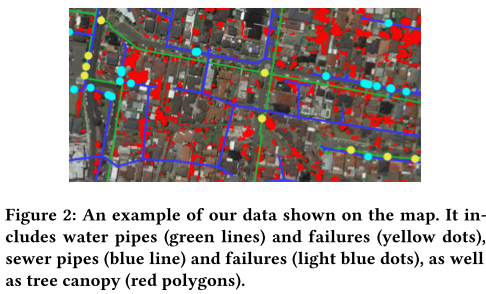
Dataset：

该文提供了两个现实世界(水和下水道)管道数据集，包括管道属性和故障记录。从水管泄漏或破裂和污水管道堵塞的角度研究管道故障。表1总结了两个数据集的基本信息。该文还从公共资源中收集土壤、海拔和树冠的数据。图2在地图上显示了部分数据。

基线：

将框架的性能与三类基线进行比较。

1. 统计模型:威布尔模型、霍克斯过程模型、随机生存森林(RSF)。

   请注意，统计模型通常将一组管道的存活可能性预测为时间的函数。我们将这种预测转化为单个管道的失效概率。

2. 基于特征的机器学习模型:随机森林(RF)、支持向量机(SVM)、梯度增强决策树(GBDT)和全连接神经网络(MLP)。

3. 基于图的gnn: plain GCN、GraphSAGE、GAT、JKGNN、DeeperGCN和DEA-GNN。

该文提出的模型在分层聚合中使用连接、LSTM或max池的MAG分别缩写为MAG- concat、MAG-LSTM或MAG- max。此外，该文还记录了使用没有地理边的图结构的MAG-nonGeo的结果。

评估标准：

使用四个基本指标，包括AUC、F1分数、Precision和Recall来比较模型的性能。此外，这项工作的目标是找到具有高失效风险的管道。因此，在验证步骤中，预计预测器会将失败的管道排在正常管道之前。在这项工作中，我们使用检测率来衡量模型的排名性能。rate@𝑘的正式定义为:
$$detectionrate@k=\frac{N_{detected}(k)}{N_{total}}\text{\hspace{1em}(10)}$$

实现细节：

方法是基于Pytorch实现的。采用Adam优化器，其批大小$\in [50\sim 2000]$，学习率$\in${0.001 ~ 0.0001}，dropout rate$\in$​{0,0.1,0.2,0.5}。为了稳定快速的训练，实现了批归一化。当验证集上的AUC超过50 epoch没有增加时，停止优化过程。利用优化后的模型进行了测试。随机抽取验证集和测试集，重复实验10次，报告平均结果。在一台带有NVIDIA A100 GPU、32核CPU和256 GB RAM的机器上运行所有实验。

4.4 实验结果

实验结果：

表4总结了两个数据集的结果。这表明基于特征的机器学习算法始终优于统计模型。在传统的机器学习模型中，GBDT达到了最好的效果。使用一个变体实现GBDT，即XGBoost，它是一个可证明的强大决策树模型。它在许多工业应用和数据科学任务中获得了最先进的结果，特别是对于包含许多分类特征的数据。对于基于GNN的基线，GCN和GraphSAGE的性能较差。这两种方法的表现都不如GBDT。原因之一是GCN中的信息聚合策略是平均的，这可能会逐渐冲刷掉管道失效预测的有用信息。GraphSAGE在聚合阶段使用了连接方案，这使得它的性能优于GCN。GraphSAGE虽然保留了第一层节点的原始特征，但它与深层没有残留的连接，并且存在与GCN相同的过平滑问题。DEA-GNN是多跳GNN的一种形式。它的性能略好于GraphSAGE，后者展示了多跳聚合的强大功能。然而，DEA-GNN没有使用注意机制或剩余连接等方法来解决过度平滑问题，性能不如GBDT。

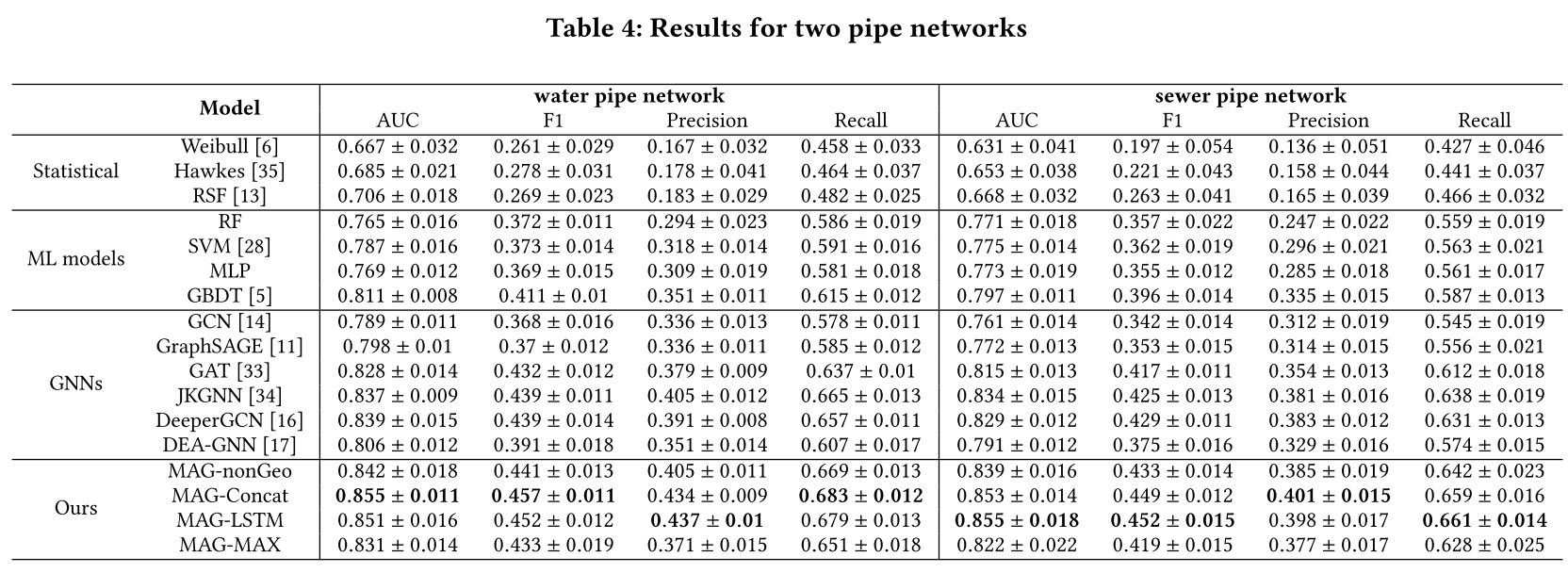
GAT、JKGNN和DeeperGCN优于其他基线。GAT在每个GNN层的聚合过程中采用了多节点关注机制，可以突出相关程度较高的邻居信息，同时抑制相关程度较低的节点的贡献。其结果表明，在将gnn应用于实际图应用时，注意机制的重要性，例如，在管道具有不同属性的管道网络中进行故障预测。JKGNN和DeeperGCN在所有基线中性能最好。它们都使用残差方案和注意力聚集来克服gnn中存在的问题。

对于该文提出模型的变体，MAG-Concat和MAG-LSTM在两个数据集上都产生了最好的性能。在实践中，MAGLSTM比magc - concat具有更多的可训练参数，因此需要支付额外的计算成本。magg - nongeo优于最佳基线，但低于magg - concat和MAGLSTM。MAG-nonGeo采用不考虑地理相邻效应的图结构。框架的GNN架构与JKGNN和DeeperGCN非常相似。MAGnonGeo仍然优于它们，这表明该模型学习的时间失效表示对失效预测有明显的影响。MAG-MAX的性能优于GAT，而不及JKGNN和DeeperGCN的最佳性能。这可能是因为分层最大池聚集会使表示产生偏差，不适合用于管道故障预测。

4.5 结果分析

聚合方法的灵敏性

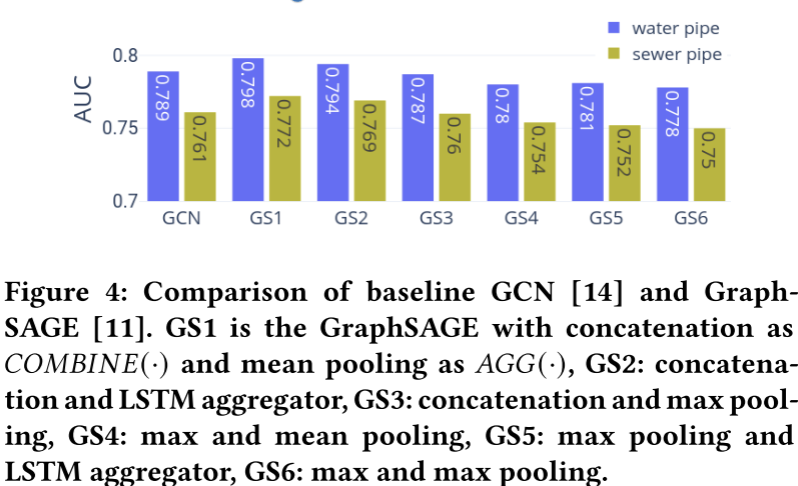
为了研究在GNN层(Eq. 2)设置中，$COMBINE(\cdot )$&$AGG(\cdot )$方法(表3)的敏感性，该文研究了两个基线GNN(即plain GCN和GraphSAGE)在两个真实管道数据集上的性能。对比结果如图4所示。其中，拼接表示为$COMBINE(\cdot )$、均值池表示为$AGG(\cdot )$的GraghSAGE效果最好，其次为LSTM-aggregator。GCN显示了第三好的结果，并且在最大池设置下优于GraphSAGEs。

该结果覆盖了数据集的几个特征。首先，连接的良好性能意味着管道本身的特征在故障预测中起着至关重要的作用。其次，两个数据集中大多数管道的度数为2，即一个管道只连接两个管道。Mean-pooling aggregation的性能略优于LSTM-aggregator，这表明Mean-pooling可能更适合我们的数据集，而大多数节点的度对于LSTM-aggregator来说太小了。此外,max-pooling都不适合$COMBINE(\cdot )$和$AGG(\cdot )$。这可能是因为最大池化选择了邻居的最大特征，并“洗掉”了目标管道的重要属性，特别是考虑到管道故障对管道属性(如长度、大小、年龄等)高度敏感。

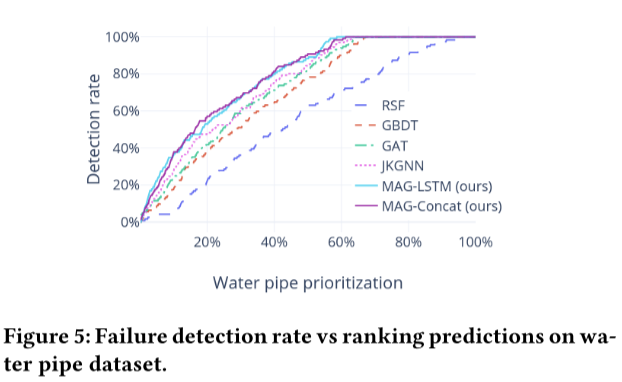
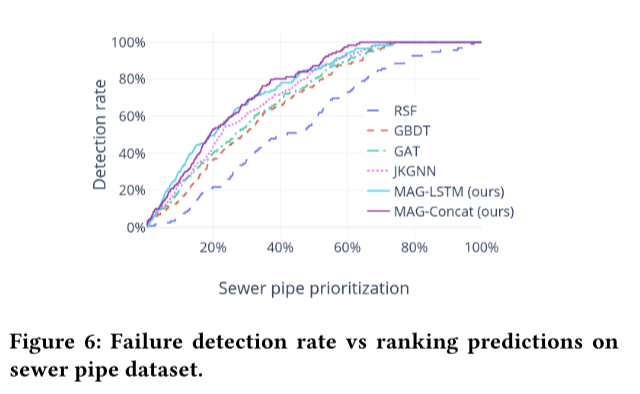
故障检测率

检测率的性能对实际管道的优先级排序具有重要意义。主动维护通常非常耗时，并且需要大量的财务和人力成本，特别是对于大型管网。决策者非常关注排名预测中高风险管道的检出率。图5和图6分别显示了水和下水道数据集在顶级预测中的检测率。RSF表现最差，这与之前的研究结果一致。人们已经认识到，统计模型更适合长期管道管理规划，但与基于特征的模型相比，统计模型在管道级预测方面的竞争力较弱。总体而言，与最佳基线JKGNN相比，该框架框架将检测率提高了约10%。更重要的是，所提出的框架在排名前20%的管道中检测到50%以上的故障。

超参数以及训练时间

表5总结了框架的最佳调优超参数。Def. 4.1中的$\rho$限制了将管道视为地理相邻的距离范围。水管是100𝑚，下水道是45m。这可能是因为大多数下水管道比大多数水管短。两个数据集的最佳批处理规模分别为1500和1000。这可能是由于所使用数据集中的极端标签不平衡，其中大多数管道没有失败。

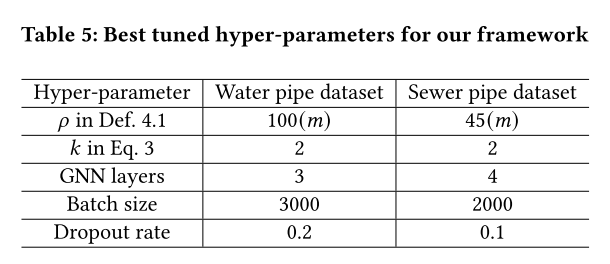
该框架可以在一台使用NVIDIA A100 GPU、32核CPU和256G RAM的机器上使用批处理归一化进行优化，大约需要10个小时，当我们将所有数据放在RAM上(RAM的最大使用量高达124G)时，使用不到2分钟的时间预测所有管道(表1)。

5. 结论

这项工作中开发了一个基于gnn的管网故障预测框架，该框架综合考虑了管网的特征、结构、地理邻近效应和历史故障信息。该文提出了一种基于管道之间的物理连接和地理距离来构建图结构的新方法。模型采用多跳聚合、各GNN层的注意机制以及最后一层后的剩余连接和分层聚合来解决GNN的问题。在框架中开发了一个时序故障模式学习模块来学习基本演化效应和历史故障对管道状态的时间衰减激励。提出的预测模型在两个实际管网上进行了评估，并获得了最先进的结果。该框架的主要任务是生成管道优先级，为水务公司提供数据驱动的管道维护支持。此外，还研究了特征重要性，这可以帮助水务专家进一步识别和了解失效原因。该框架可以扩展到大规模的基础设施网络，用于资产级故障预测。

小结

这项工作基于两个现实世界的大型管网。该文框架在这些数据集上进行了评估，实验结果表明，它优于统计和机器学习模型，以及最先进的GNN基线。所提出的框架嵌入到已实施的平台中，为主动维护提供重要的数据驱动支持，例如定期管道检查、管道更新计划和管道故障原因研究。该文还使用模型研究了特征的重要性，这有助于领域专家识别和理解导致管道失效的物理因素。

参考文献

[1] Shuming Liang; Zhidong Li; Bin Liang; Yu Ding; Yang Wang; Fang Chen; Failure Prediction for Large-scale Water Pipe Networks Using GNN and Temporal Failure Series. https://dl.acm.org/doi/10.1145/3459637.3481918