备战秋招60天算法挑战，Day22

news2025/1/12 16:18:08

题目链接： https://leetcode.cn/problems/missing-number/

视频题解： https://www.bilibili.com/video/BV1HS42197Hc/

LeetCode 268.丢失的数字

题目描述

给定一个包含 [0, n] 中 n 个数的数组 nums ，找出 [0, n] 这个范围内没有出现在数组中的那个数。

举个例子：

输入：nums = [3,0,1]
输出：2
解释：n = 3，因为有 3 个数字，所以所有的数字都在范围 [0,3] 内。2 是丢失的数字，因为它没有出现在 nums 中。

视频题解

丢失的数字

思路来源

思路解析

方法一位运算

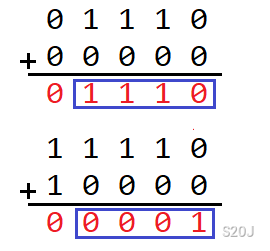
首先来看一下异或运算的特点，11转成二进制1011，13转成二进制1101，它们之间的异或运算如下图：

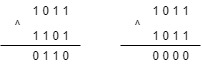
11 ^ 13 = 6，11 ^ 11 = 0，可以看出，对于二进制相同的bit位按位异或值是0，比如1 ^ 1 = 0，0 ^ 0 = 0。不同值bit位按位异或值是1，比如1 ^ 0 = 1。

利用异或运算符这个特性我们可以轻松解决这个题目。

对区间[0, n]和数组nums中所有的元素做异或运算，在nums中的元素会出现两次，不在nums中的元素只会出现一次，两个相同的元素做异或值为0，最后的结果就是不在nums中的元素。

比如n = 3，nums = [3, 0, 1]。0 ^ 1 ^ 2 ^ 3 ^ 3 ^ 0 ^ 1 = (0 ^ 0) ^ (1 ^ 1) ^ (3 ^ 3) ^ 2 = 0 ^ 2 = 2。最终2就是不在nums中的数字。

C++代码

class Solution {
public:
    int missingNumber(vector<int>& nums) {
        int nums_len = nums.size();
        int res = nums_len;
        for (int i = 0; i < nums_len; ++i) {
            //[0,n]和nums中的元素做异或操作
            res ^= (i ^ nums[i]); 
        }
        return res;
    }
};

java代码

class Solution {
    public int missingNumber(int[] nums) {
        int nums_len = nums.length;
        int res = nums_len;
        for (int i = 0; i < nums_len; ++i) {
            //[0,n]和nums中的元素做异或操作
            res ^= (i ^ nums[i]);
        }
        return res;
    }
}

python 代码

class Solution:
    def missingNumber(self, nums: List[int]) -> int:
        nums_len = len(nums)
        res = nums_len
        for i in range(nums_len):
            #[0,n]和nums中的元素做异或操作
            res ^= (i ^ nums[i])
        return res

方法二数学运算

因为区间[0, n]上有n + 1个元素，数组nums中只有n个元素，假设缺失的元素为X，我们可以得到如下公式：

0 + 1 +...+ n = nums[0] + nums[1] +...+ nums[n-1] + X

我们只需要用区间[0, n]所有元素的和减去nums中所有元素的和就得到最终的结果X。

C++代码

class Solution {
public:
    int missingNumber(vector<int>& nums) {
        int nums_len = nums.size();
        int res = nums_len;
        for (int i = 0; i < nums_len; ++i) {
            //[0,n]的和减去nums中所有元素的和
            res += (i - nums[i]); 
        }
        return res;
    }
};

java代码

class Solution {
    public int missingNumber(int[] nums) {
        int nums_len = nums.length;
        int res = nums_len;
        for (int i = 0; i < nums_len; ++i) {
            //[0,n]的和减去nums中所有元素的和
            res += (i - nums[i]);
        }
        return res;
    }
}

python代码

class Solution:
    def missingNumber(self, nums: List[int]) -> int:
        nums_len = len(nums)
        res = nums_len
        for i in range(nums_len):
            #[0,n]的和减去nums中所有元素的和
            res += (i - nums[i])
        return res