在上一篇文章已经介绍了opencv特征检测中的一些必要的概念,介绍了什么是特征,什么是角点,这些角点特征可以做什么。今天来看看对于我们人来说很容易就识别到角点特征,对于计算机来说是如何识别的,具体的步嘴原理是怎样的。
一、计算机中的角点
在众多的检测算法里最经典的角点特征检测就是Harris角点检测,它是一个特别好的方法,由Chris Harris和Mike Stephens于1988年提出。角点是图像中两条边缘的交点,通常具有两个主要特征:高响应和多方向性。也就是将整个图形角点的检测分成三种情况,如下图所示。

- 对于第一种情况 ,检测窗口朝任意方向进行移动,在任何方向进行移动之后,窗口内的像素没有任何差异的变化,这说明这是一个平坦的区域,也就是说没有检测到角点特征。
- 对于第二种情况,检测窗口在边缘上,沿着边缘的方向进行移动。虽然边缘的像素和周围的像素是不同的,但是检测窗口是沿着边缘移动,中心像素是没有明显的差异变化;但如果检测窗口不是沿着边缘移动,譬如是垂直边缘进行移动,中心像素会剧烈的变化。这可以简单的确定为边缘特征。
- 对于第三种情况,检测窗口在角点上,中心像素已经在角点上,那么在这个窗口内无论朝哪个方向移动的时候都会产生剧烈的变化,这个时候就可以简单的确定为角点特征了。
以上介绍的特征情况,对于计算机来说去做判断其实是不容易的,我们需要以数学的方式去总结以上三种特征情况,对应如下三点:
- 局部小窗口沿各方向移动,窗口内的像素均产生明显变化的点。
- 图像局部曲率(梯度)突变的点。
- 对于同一场景,即使视角发生变化,其角点通常具备某些稳定不变性质的特征
有了基本的对角点的数学描述,我们可以进一步把它转化为数学公式描述:

其中公式的参数解释分别如下:

- 目标输出代表:统计窗口内整体像素值变化,是一个标量。
- 窗口向水平方向移动的像素距离(u);窗口向水平方向移动的像素距离(v)
- 检测窗口的长和宽是x和y的取值范围
- I (𝑥,𝑦) 表示窗口内 (𝑥,𝑦) 处的像素值, I (𝑥+𝑢,𝑦+𝑣) 表示原窗口中 (𝑥,𝑦) 处像素在窗口移动后对应位置的像素值
- 𝑤(𝑥,𝑦) 表示窗口内 (𝑥,𝑦) 处的位置权重
其函数的物理意义简单描述为:计算了窗口移动 (u,v)的像素距离前后,其内每个像素值变化的平方(之所以要平方,是为了使变化度量值非负)并将这些变化值加权求和,权重与窗内位置有关。得到的函数就表示了我们所想观察的“区域信息的变化特征”。
但如果我们此时用以上公式进行角点检测,会发现其中的参数u和v没有明确的规定,也就是窗口移动的方向。如果人为的规定u和v,这样一样,指定方向窗口滑动又可能导致检测出来的角点其实是边缘点;那么我们可以指定若干组的u和v,即不同的窗口滑动方向,对所有的u和v求得E再进行统计计算,完美。
然而事实上Harris角点检测并没有这么做。Harris可能在想,应该如何优化这个原始的检测函数呢,提高精度,降低计算的复杂度呢?
二、Harris角点检测算法的演变
原始的函数在计算上显得有些复杂了,Harris发现在不改变函数的物理意义的情况下可以将函数变得更直观。
原E(u,v)是一个二元函数,对E(u,v)进行一阶的泰勒近似展开得出如下的表达式。

关于泰勒级数展开,我搞了一篇文章简单记录其知识点。然后我发现网上有一部分教程,是用泰勒二阶展开来分析,但我个人感觉一阶展开在分析的时候更容易入手。近接着上图第一个约等号后,剩余的数学推导如下图:

所以E(u,v)能量表达式可以简化更新为如下公式,而其中的 Ix 和 Iy 对于图像来说就是水平方向和竖直方向的梯度了。

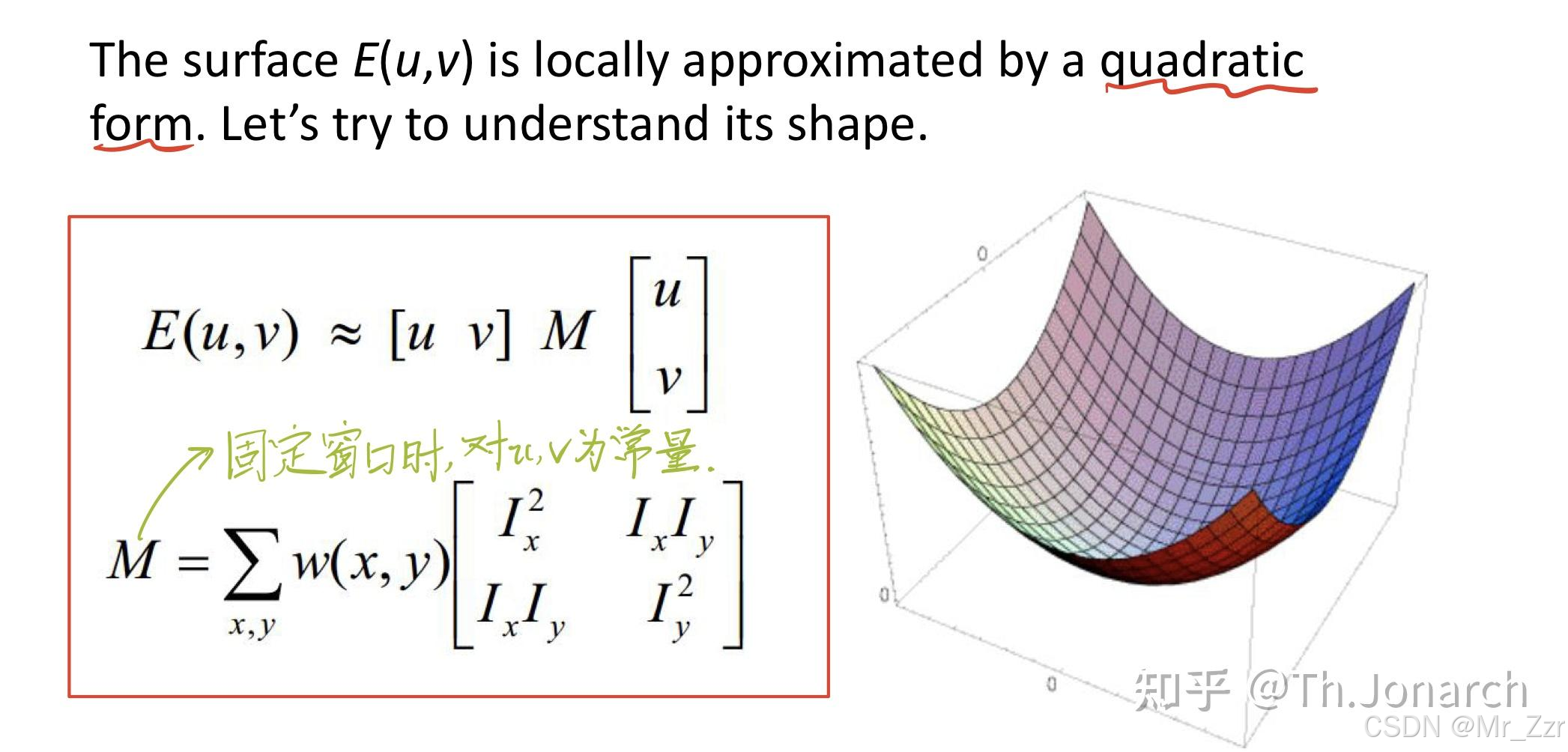
公式虽然是简化了,难道就可以直接用来检测角点了吗?首先我们回到最初E(u,v)能量表达式的物理意义:E的大小表示窗口移动导致的窗口整体内容的变化程度大小。之前在分析角点特征就提到,对角点来说,它是两个或多个边缘的交点,边缘的特征是梯度在某一方向变化近似为0,那么这个交点应该表现为某一区域内有两个或多个方向上的“边缘性变化”的梯度信息。
我们注意到角点区域的像素会有“两个或多个方向”上的“边缘性变化”的梯度信息,刚好和这里的“x和y两个方向上的梯度信息”产生了联系,我们可以先假设角点区域只在x和y两个相互垂直的方向上有较为明显的变化,那么梯度信息就会有如下表现:

由上图可知,在“假设角点区域只在x和y两个相互垂直的方向上有较为明显的变化”之后,如果一个区域是角点区域,那么其梯度方向就会集中在x和y两个垂直的方向上,对于窗口内绝大多数像素点来说,要么y方向的梯度趋近0,要么x方向的梯度趋近0,两个方向的梯度的乘积也就趋近0了。对所有像素点进行累加,因为绝大多数像素点的“两个方向的梯度的乘积趋近0”,M矩阵经累加操作后,反对角线上的两个值( Ix Ix )也就趋近于0。
但假设归假设,真实图像上的角点不可能两个边缘就是相互垂直的,但其实我们可以做一个仿射变换,因为做角点检测我们也不在乎角点的方向。把两个边缘的变换到【假设的规范坐标系上】,检测完之后再逆变换还原就可以了。所以当角点区域的梯度集中在任意两个垂直的方向上时,我们对M进行相似对角化,总能得到以下结果:
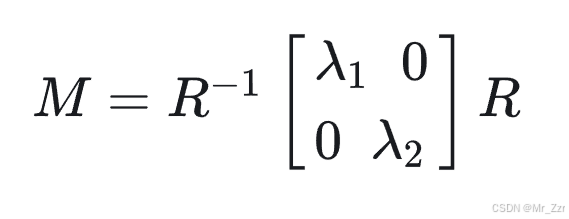
这个时候,我们回到那个评价函数E的形状上去,看看M怎样决定了这个形状,我们又一个怎样将函数形状的特点与角点区域特征对应起来。

如上图,若让函数E取一个函数结果值,譬如1,那么会得到一个方程,这个方程表示了E函数图像的水平切片上,根据上图中那个不太严谨的变换,可以看出这是一个椭圆方程。


上面的式子总结为椭圆的数学公式,𝜆1和𝜆2的大小决定长短轴, 那么这个椭圆有啥用呢?水平切片总结的椭圆公式其实就是E函数的表现,具体如下:

如上图,这里对𝜆1和𝜆2的大小关系进行分类讨论,强调:𝜆1和𝜆2的大小反应两个垂直方向的梯度信息集中强度。
- 如果两个值都大,且相差不大,则“E函数水平切片椭圆”趋近于圆,区域梯度在两个垂直的方向都有较强集中度,所以是角点区域。而对于其R值,则是要大于0且绝对值较大的时候,我们判断为角点区域。
- 如果其中一个值远大于另一个值,则,则“E函数水平切片椭圆”趋近于线,区域梯度只在一个方向上有较强集中度,所以是边缘区域。而对于其R值,则是要小于0且绝对值较大的时候,我们判断为边缘区域。
- 如果两个值都很小,则“E函数水平切片椭圆”趋近于点,区域梯度信息在两个方向都较弱,所以是像素值平坦区域。而对于R值,则是要接近于0的小数且绝对值较小的时候,我们判断为平坦区域。
以上就是Harris角点检测,角点区域的量化判定方法的演算过程,之后我们就可以方便的利用算法,对二维图像进行角点检测。
三、OpenCV的Harris角点检测
根据上述的讨论,我们总结出Harris角点算法的基本步骤,我们试着手动实现Harris角点检测:
1、计算窗口中各像素点在x和y方向的梯度;
2、计算两个方向梯度的乘积,即Ix ^ 2 , Iy ^ 2 , IxIy(可以用一些一阶梯度算子求得图像梯度)
3、使用滤波核对窗口中的每一像素进行加权,生成矩阵M和元素A,B,C
4、计算每个像素的Harris响应值R,并对小于某阈值的R置0;
5、由于角点所在区域的一定邻域内都有可能被检测为角点,所以为了防止角点聚集,最后在3×3或5×5的邻域内进行非极大值抑制,局部最大值点即为图像中的角点。
在手写Hairrs角点检测前,看看OpenCV内置的Hairrs角点检测的函数为cornerHairrs(),但是它的输出是一幅浮点值图像,浮点值越高,表明越可能是特征角点,我们需要对图像进行阈值化。
CV_EXPORTS_W void cornerHarris( InputArray src, OutputArray dst, int blockSize,
int ksize, double k,
int borderType = BORDER_DEFAULT );- src – 输入的单通道8-bit或浮点图像。
- dst – 存储着Harris角点响应的图像矩阵,大小与输入图像大小相同,是一个浮点型矩阵。
- blockSize – 邻域大小。
- ksize – 扩展的微分算子大,也就是求梯度的窗口大小。
- k – 响应公式中的,参数α(0.04~0.06)。
- boderType – 边界处理的类型。
void harris_detaction(int, void*)
{
Mat det_mat, normal_det_mat;
det_mat = Mat::zeros(gray_src.size(), CV_32FC1);
int blockSize = 3; // 加权的检测窗口size
int ksize = 3; // 求梯度的size
if (SELF_HARRIS) {
my_cornerHarris(gray_src.clone(), det_mat, ksize, 0.04);
}
else {
cornerHarris(gray_src.clone(), det_mat, blockSize, ksize, 0.04);
}
//阈值化Harris检测结果,0.001为分割阈值
threshold(det_mat, normal_det_mat, 0.001, 255, THRESH_BINARY);
//将Harris响应值转为整型(uchar)
convertScaleAbs(normal_det_mat, normal_det_mat, 1, 0);
// show detection.
Mat result = src.clone();
for (int r = 0; r < result.rows; r++) {
for (int l = 0; l < result.cols; l++) {
int det_value = normal_det_mat.at<uchar>(r, l);
if (det_value > 0) {
circle(result, Point(l, r), 1, Scalar(0, 0, 255), 2);
}
}
}
imshow("Harris", result);
}Opencv-Harris检测结果如下图红点位置。

void my_cornerHarris(Mat src, Mat& dst, int ksize, double k)
{
Mat Ix, Iy; //存储图像一阶梯度
Mat M(src.size(), CV_32FC3); //创建3通道矩阵M存储 Ix*Ix , Ix*Iy , Iy*Iy
Mat R(src.size(), CV_32FC1); //创建3通道矩阵R存储Harris响应值
//使用Sobel算子提取图像x方向梯度和y方向梯度
Sobel(src, Ix, CV_32FC1, 1, 0, ksize);
Sobel(src, Iy, CV_32FC1, 0, 1, ksize);
//存储Ix*Ix , Ix*Iy , Iy*Iy
for (int i = 0; i < src.rows; i++) {
for (int j = 0; j < src.cols; j++) {
M.at<Vec3f>(i, j)[0] = Ix.at<float>(i, j) * Ix.at<float>(i, j); //Ix*Ix
M.at<Vec3f>(i, j)[1] = Ix.at<float>(i, j) * Iy.at<float>(i, j); //Ix*Iy
M.at<Vec3f>(i, j)[2] = Iy.at<float>(i, j) * Iy.at<float>(i, j); //Iy*Iy
}
}
//高斯滤波对M矩阵进行加权求和
GaussianBlur(M, M, Size(ksize, ksize), 2, 2);
//求得Harris响应值
for (int i = 0; i < src.rows; i++) {
for (int j = 0; j < src.cols; j++) {
float A = M.at<Vec3f>(i, j)[0]; //Ix*Ix
float C = M.at<Vec3f>(i, j)[1]; //Ix*Iy
float B = M.at<Vec3f>(i, j)[2]; //Iy*Iy
//响应值计算公式:矩阵的行列式的绝对值等于其所有特征值之积的绝对值。
R.at<float>(i, j) = (A * B - C * C) - (k * (A + B) * (A + B));
}
}
dst = R.clone();
}
void nms(Mat& src)
{
int i, j, k, l = 0;
//遍历图像
for (i = 2; i < src.rows-2; i++)
for (j = 2; j < src.cols-2; j++)
//采用5×5窗口,小于中心像素置零
for (k = i - 2; k <= i + 2; k++)
for (l = j - 2; l <= j + 2; l++)
if (src.at<float>(k, l) <= src.at<float>(i, j) && k != i && l != j && src.at<float>(k, l) > 0)
src.at<float>(k, l) = 0;
}这里我也尝试自己实现my_cornerHarris,基本代码如上,输出的是0~255的规范值,所以输出后阈值化检测结果的阈值得换成[0,255]之间的数值,还得经过局部非极大值抑制nms处理,要不然会看到很多重复的点位置。
以上就是Harris角点检测,我知道的。
参考链接:
怎么深入了解 Harris 角点检测? - 知乎 (zhihu.com)
Harris角点详细解释_harris角点中文-CSDN博客