查找一个有向网络的头节点和尾节点 （200）

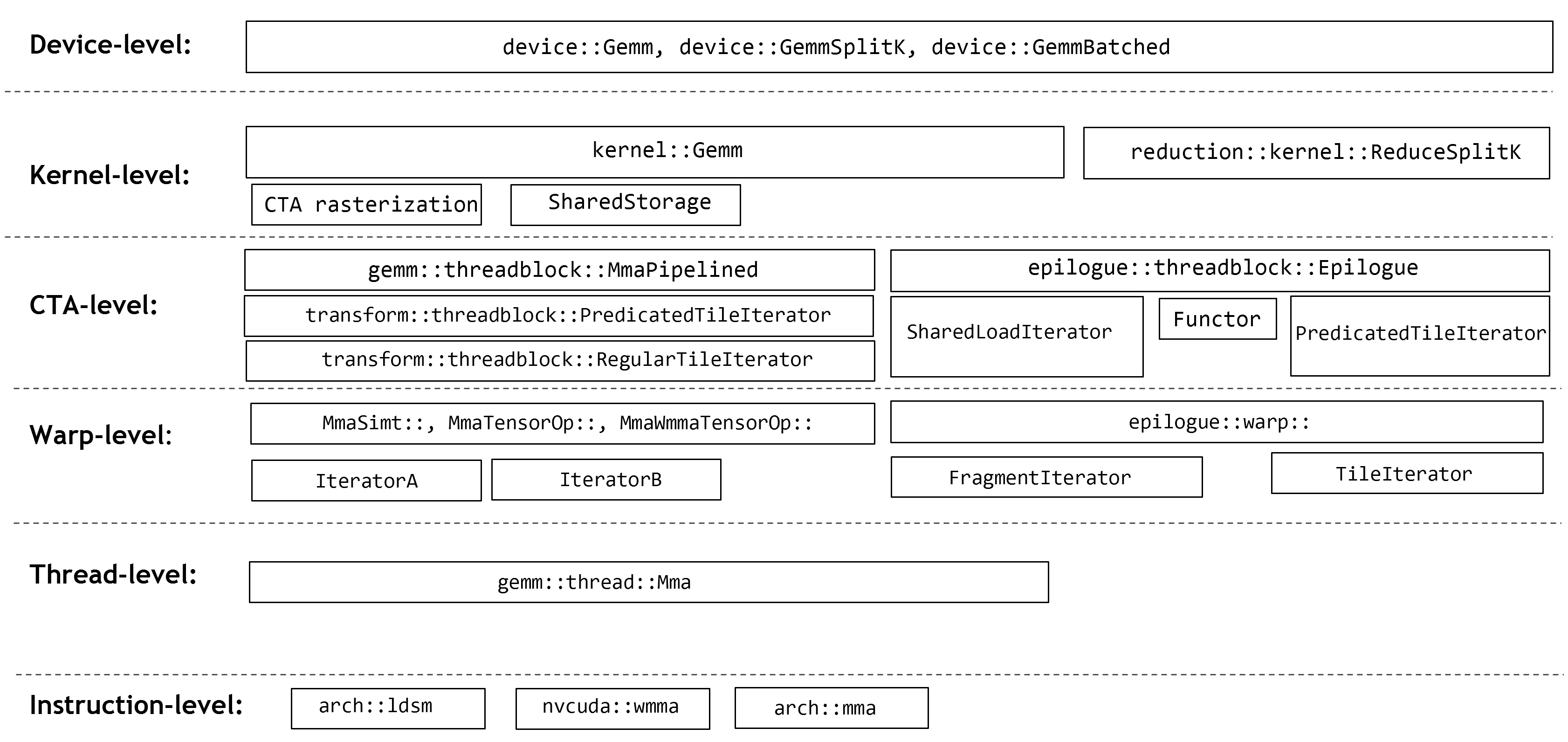
• 在一个有向图中，有向边用两个整数表示，第一个整数表示起始节点，第二个整数表示终止节点；
• 图中只有一个头节点，一个或者多个尾节点；
• 图可能存在环，有环则输出-1；
• 输出图中的头节点（入度为0）、尾节点（出度为0），如图头节点为1，尾节点为4。
  
  输入描述：
  第一行输入n，n >=0
  第二行为n个数对，表示n条边；
  输出描述：
  输出一行，头节点、尾节点以空格隔开，多个尾节点则从大到小输出。
   
  示例1
  输入：
  4
  1 2 1 3 2 4 3 4
  输出：
  1 4
   
  示例2
  输入：
  3
  1 2 1 3 1 4
  输出：
  1 4 3 2
   
  示例3
  输入：
  4
  1 2 2 3 3 4 4 1
  输出：
  -1
   
  示例4
  输入：
  5
  1 2 2 3 3 4 4 5 4 2
  输出：
  -1
  思路：
• 拓扑排序，判断有向图是否有环，有环则直接输出-1；
• 只有一个起始点，一个或多个结尾点；

# __author__ = "laufing"


class GraphHeadTail:
    def solution(self, n, edges):
        # 所有的顶点和数目
        vertex = list(set(edges))
        vertex_num = len(vertex)
        # 统计每个顶点的入度
        in_degree = {}.fromkeys(vertex, 0)
        # 每个顶点的出度
        out_degree = {}.fromkeys(vertex, 0)
        for i in range(n):
            u, v = edges[i*2:(i+1)*2]
            out_degree[u] += 1
            in_degree[v] += 1

        # 找到入度为零的一个节点
        start_node = None
        for key in in_degree:
            if in_degree.get(key) == 0:
                start_node = key
                break

        if self.topology_sort(in_degree, start_node, edges, vertex_num):
            print(-1)
            return -1

        # 无环  输出头节点 + 尾节点
        # 找到所有的尾节点
        tails = []
        for key in out_degree:
            if out_degree.get(key) == 0:
                tails.append(key)
        tails.sort(reverse=True)
        result = str(start_node) + " " + " ".join(list(map(str, tails)))
        print(result)
        return result

    def topology_sort(self, in_degree, start_node, edges, vertex_num):
        in_degree = in_degree.copy() # 不影响原始数据
        if start_node is None:
            return True
        stack = []
        output_list = []
        stack.append(start_node)

        while stack:
            nodev = stack.pop()
            print("nodev:", nodev)
            output_list.append(nodev)
            # 删除边，对应的顶点入度-1
            for i in range(len(edges) // 2):
                u, v = edges[i*2:(i+1)*2]
                if u == nodev:
                    in_degree[v] -= 1
                    if in_degree[v] == 0:
                        stack.append(v)
        print(output_list)
        return len(output_list) < vertex_num


if __name__ == '__main__':
    graph_head_tail = GraphHeadTail()
    while True:
        try:
            n = int(input("n:").strip())
            edges = list(map(int, input("edges:").strip().split()))
            graph_head_tail.solution(n, edges)
        except KeyboardInterrupt:
            break