二、时间序列的挑战

2.1 特征提取

仅选择“信息性”特征，这些特征在多变量时间序列分析中捕获重要信息和底层模式。由于时间序列数据是数据冗余的，为了增强可解释性并使模型不易过拟合，应删除冗余数据。减少数据维度可以更快地处理时间序列，并且还可用于应用机器学习技术进行有价值的预测。对于自动特征提取，可以利用各种深度学习技术，并且可能不需要太多的手动特征提取。自动特征提取的唯一挑战是它的计算量很大，而且是一个黑匣子模型，这将在解释阶段造成挑战。

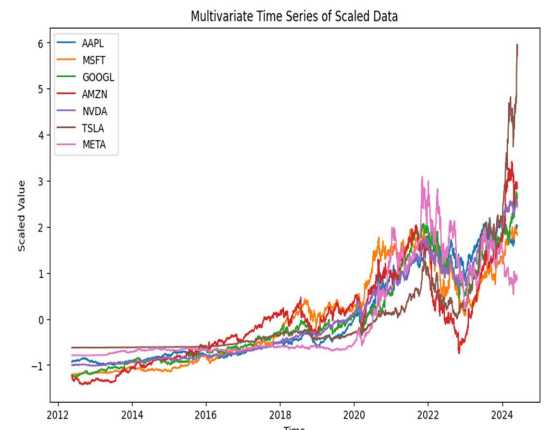
        多变量时间序列是指在特定时间点具有多个相互关联的点的数据。为了进行分析，从yfinance库中获取了宏伟的七只股票数据，并通过本文展示了一个没有任何特征工程的样本时间序列。

        多变量时间序列的主要挑战之一是它在变量之间存在相互依赖性。例如，谷歌股票的价格可能取决于苹果的价格或NVidia股票的价格。由于它是基于时间的测量，每只股票都会有一个时间戳，而多元分析强调捕捉这种相互依存关系之间的潜在关系和模式。

2.2 诊断

1. 残差图

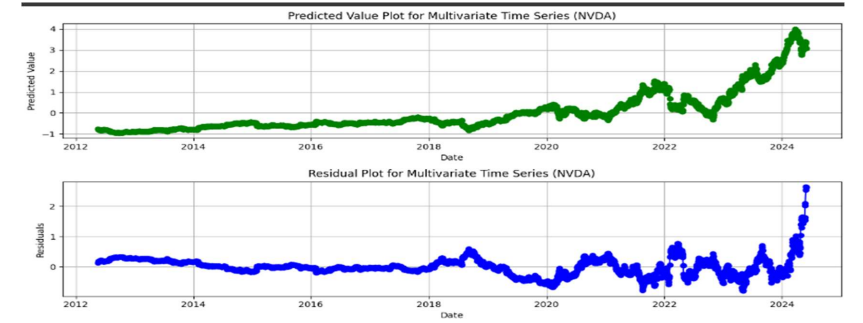
残差图

        该图显示了随时间推移的残差值以及预测值，并且两个图之间存在巨大差异。该图是使用线性回归创建的，以了解残差。残差最终会告诉模型与实际值相差多少，并有助于评估模型准确性和识别错误。特征提取的第一步从绘制残差图开始，找到任何系统错误或模式，从而通过使用更好的特征来改进模型。

2. 相关性热图

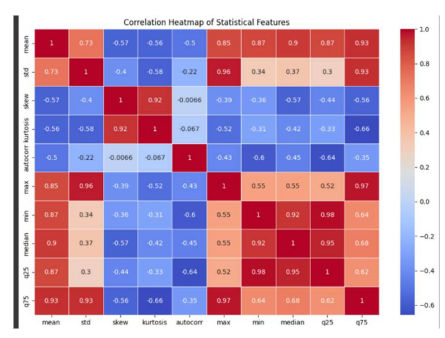
三、热图

验证特征工程需求的另一种方法是相关性图。对于统计分析，并非所有特征都是必需的，相关性图有助于确定特征如何相互关联。通过识别相关性特征，选择具有最多信息的特征子集并删除冗余特征。选择特征的经验方法之一是，如果阈值大于 0.7（即 70%），则应选择其中一个相似特征，而不是两个特征。

三、 基于机器学习的诊断

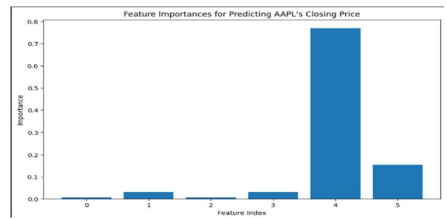
绘制特征重要性图

        对冗余或不相关数据的早期诊断有助于做出有关特征提取的明智决策。相关性热图（线性关系）存在一些挑战，为了克服这些挑战，应该使用基于机器学习的模型来发现特征的值并删除权重较低的特征。

        损害

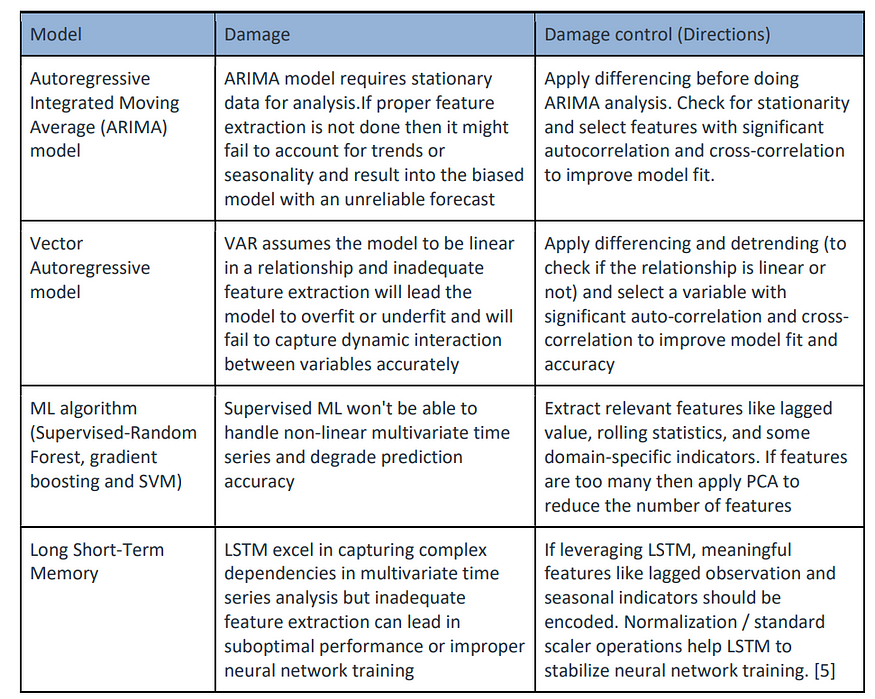
四、方向

4.1 自相关和滞后特征提取

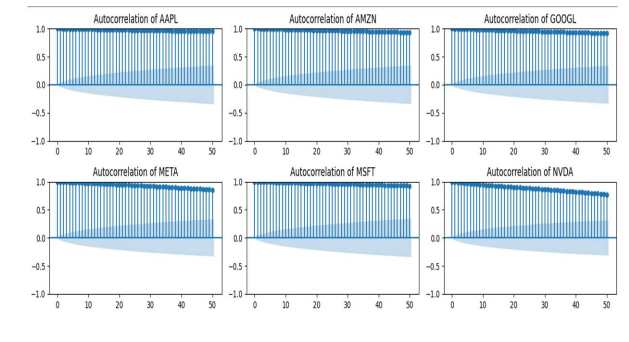
        不同股票的自相关性

        自相关：自相关是指变量在不同时间滞后下与自身的相关性，它有助于理解变量如何与其自身的过去值相关联。从视觉角度来看，显著的峰值表明数据中可能存在时间依赖性或模式。出于特征工程目的，使用 3 个滞后（1 天滞后、7 天滞后和 30 天滞后）来确定趋势/季节性或周期性模式。

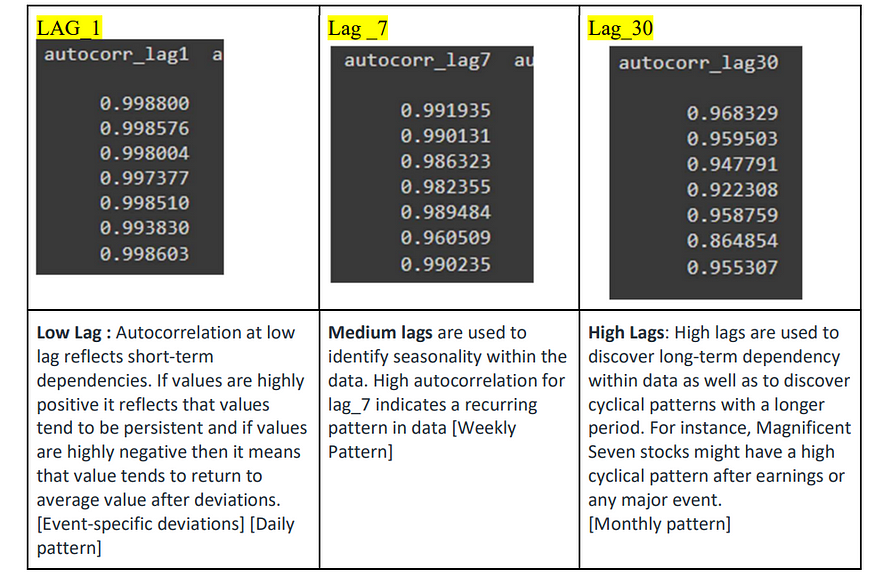
滞后特征提取

        对于特征提取：没有这样的滞后，这将被视为最佳滞后，因此必须考虑滞后组合来检测数据中的依赖性。在特征提取中，数据的可解释性比高自相关滞后更重要。

4.2. 差异

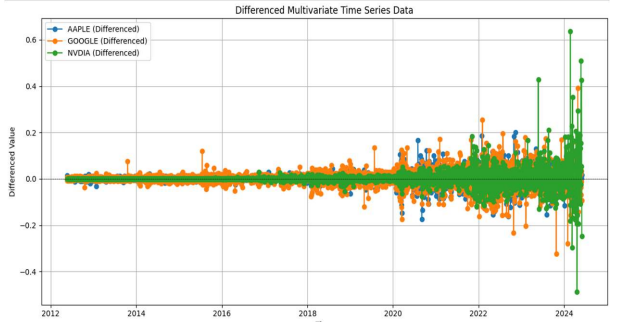
4.3、差分

        差异是一种用于转换数据以消除趋势和季节性的技术。差分涉及从当前值中减去前一个值，可以减少数据，但仍保持模式。此外，对于像 ARIMA 这样的模型，它提高了平稳性。要检查差分的必要性，首先要检查数据自身是否具有平稳性分量。要检查平稳性，请执行增强 Dickey Fuller 检验 （ADF TEST）。

4.4. 互相关

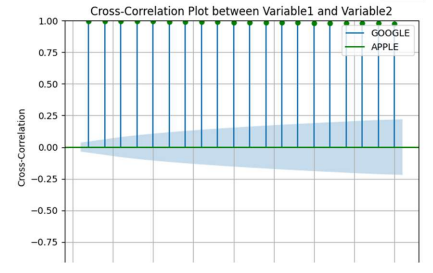
        互相关

        互相关是一种强大的技术，可以理解不同变量之间的滞后关系。与衡量整体线性关系的相关性不同，互相关侧重于相对于另一个变量的变化。通过计算互相关，它有助于预测目标变量和不同滞后的另一个变量的目标值。

4.5. 基于时间的特征提取

        滚动均值：有助于突出潜在趋势，并减少整体噪音

        滚动标准差：有助于突出波动性，并补充滚动均值

4.6. 基于形状的特征提取

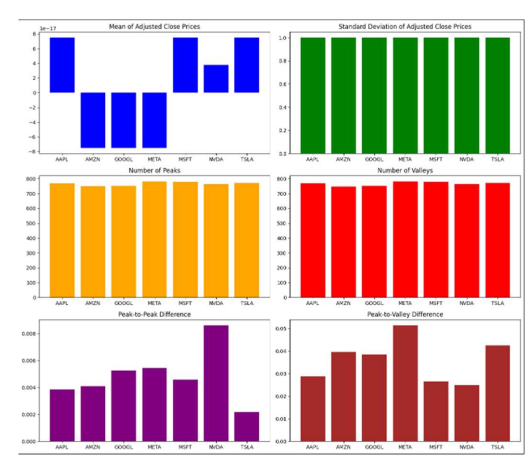
        基于形状的特征提取

        峰值和谷值计数捕获了事件的总体频率，并可能指示波动性水平的变化。峰与峰值之差是最高值和最低值之间的绝对差值，峰与谷之差是峰和最接近谷值之间的绝对差值。这种基于形状的特征提取用于理解特征工程的数据特征，同时它还提供了有关噪声敏感性和任务特定相关性的想法。

4.7、主成分分析

        PCA 通过减少维度和捕获数据中的最大方差来帮助特征提取。

1  自动特征提取（神经网络）

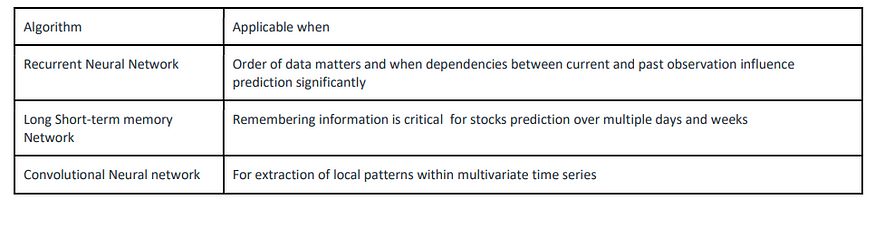
2 基于神经网络的模型的特征提取

在下文中，上给我写关于我的文章的反馈