【系统分析师】-综合知识-数据库基础

news2024/9/22 17:27:33

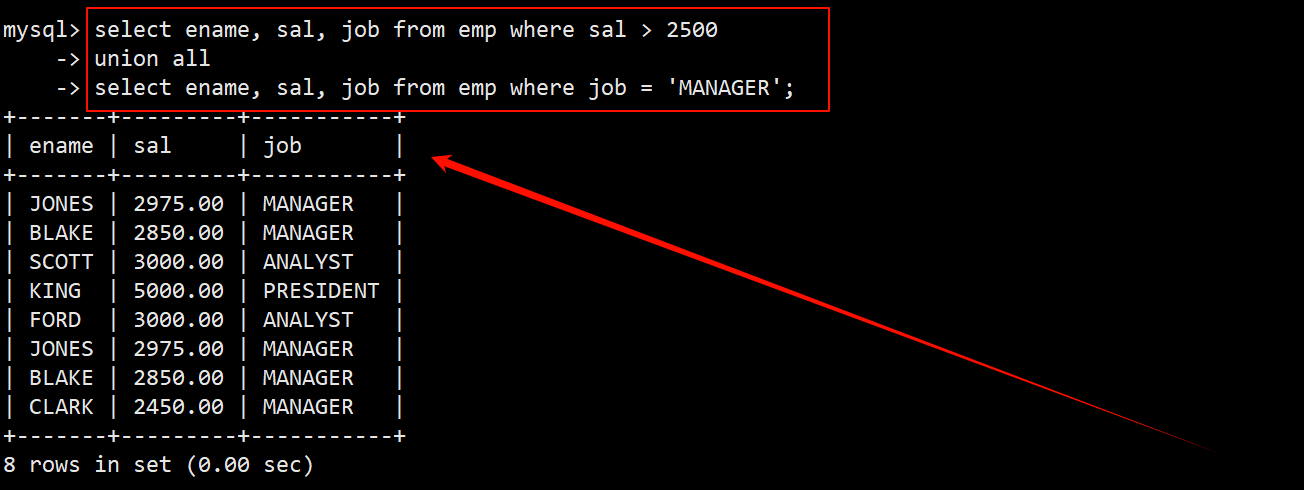
1、给定关系模式 R < U ，F >， U= {A，B，C，D ，E} ， F = {B→A ，D→A ，A→E ，AC→B }，则 R 的候选关键字为（CD），分解ρ= {Rl（ABCE），R2（CD)}

CD能推出题中关系式的所有属性，因此 R 的候选关键字为CD。判断是否为无损连接，首先进行R1∩R2=C，由于C不能推出R1或者R2中的任何属性值，因此该分解为有损分解。原关系式F 中有D→A 而分解的Rl（ABCE）中没有D，所以该分解不保持函数依赖。

2、

44题选项A的“∨”应该改为“∧”；选项B与选项C不应该是笛卡尔积。自然连接与笛卡尔积的区别是：自然连接去掉了重复的属性列。

3、假设关系 R(A1,A2,A3)上的一个分解为ρ={(A1,A2),(A1,A3)}，下表是关系 R 上的一个实例，根据实例推出 R 的函数依赖集 F 为（F={A1A3→A2,A1A2→A3}），分解 p（请作答此空）。

A1是a，A2可以是a或b或c，无法确定唯一字符，但是A1A3的组合可以唯一确定A2，A1A2的组合同理。

判断是否为无损连接，首先进行(A1A2)∩(A1A3)=A1，因为A1无法唯一确定A2、A3，因此该分解为有损连接。

4、关系R、S如下表所示，R÷（πA1,A2(σ 1<3(S)))的结果为( {4} )。

R、S的左外联接、右外联接和完全外联接的元组【记录行】个数分别为(4,4,6)。

关系代数的除法运算是同时从关系的水平方向和垂直方向进行运算的。若给定关系R(X，Y)和S(Y，Z)，X、Y、Z属性组，R÷S应当满足元组在X上的分量值x的象集Yx包含S在Y上投影的集合。记作：

其中：Yx为x在R象集，x=tr[X]。且R÷S的结果集的属性组为X。

根据除法定义，X属性为A3，Y属性为(A1,A2)，R÷S应当满足元组在X上的分量值x的象集Yx包含S在Y上投影的集合，所以结果集的属性为A3。属性A3可以取3个值{3，4，7}，其中：3的象集为{(1，2)}，4的象集为{(2，1)，(3，4)}，7的象集为{(4，6)}。

根据除法定义，本题关系S为（πA1A2(σ 13(S))，在属性组Y(A1A2)上的投影为{(2，1)，(3，4)}

左外联接是指R与S进行自然连接时，只把A中舍弃的元组放到新关系中。

右外联接是指R与S进行自然连接时，只把S中舍弃的元组放到新关系中。

完全外联接是指R与S进行自然连接时，把尺和^中舍弃的元组都放到新关系中。

5、某集团公司下属有多个超市，假设公司高管需要从时间、地区和商品种类三个维度来分析某电器商品销售数据，那么应采用（ OLAP ）来完成。

在OLAP中，数据通常是多维的

6、建立一个供应商、零件数据库。其中“供应商”表S(Sno，Sname，Zip，City)中的元素分别表示供应商代码、供应商名、供应商邮编、供应商所在城市，其函数依赖为：Sno→(Sname，Zip，City)，Zip→City。

a. “供应商”表S属于（1）。

b.若要求：供应商代码不能为空，且值是唯一的，供应商的名也是唯一的：零件号不能为空，且值是唯—的；一个供应商可以供应多种零件，而一种零件可以由多个供应商供应。请将下面的SQL语句空缺部分补充完整。

CREATE TABLE S(Sno CHAR(5) (NOT NULL UNIQUE),

Sname CHAR(30) UNIQUE,

Zip CHAR(8),

City CHAR(20),

PRIMARY KEY(Sno));

供应商表S属于2NF，因为表S的主键是Sno，非主属性Sname，Zip，City不存在对主键的部分函数依赖。但是，当2NF消除了非主属性对主键的传递函数依赖，则称为3NF。供应商表S不属于 3NF，因为存在传递依赖，即Sno→ Zip，Zip →City。

7、设有员工实体Employee （employeelD，name，sex，birth，age，tel，departID），其中employeelD为员工号，name为员工姓名，sex为员工性别，age为员工年龄，birth为员工出生日期，tel为员工电话，记录该员的手机号码、办公室电话等，deparlD为员工所在部门号，参照另一部门实体Department的主键departID。Employee实体中存在派生属性（1）。Employee实体中还存在多值属性（2）。对属性 departID的约束是（3）。