文章目录
- 希尔排序
- 希尔排序的时间复杂度计算
希尔排序
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数(通常是gap = n/3+1),把待排序文件所有记录分成各组,所有的距离相等的记录分在同一组内,并对每一组内的记录进行排序,然后gap=gap/3+1得到下一个整数,再将数组分成各组,进行插入排序,当gap=1时,就相当于直接插入排序。它是在直接插入排序算法的基础上进行改进而来的,综合来说它的效率肯定是要高于直接插入排序算法的。

第一趟排序:
n=10,gap=n/2=5分成五组,每组都用直接插入排序。
end一开始放在9的位置上,tmp放在4的位置上第二趟排序:
gap=5,gap=gap/3+1=2分成两组,每组都用直接插入排序。
end一开始放在4的位置上,tmp放在2的位置上第三趟排序:
gap=2,gap=gap/3+1=1直接插入排序
希尔排序的特性总结
希尔排序是对直接插入排序的优化。
当
gap > 1时都是预排序,目的是让数组更接近于有序。当
gap == 1时,数组已经接近有序的了,直接插入排序。
代码实现:
Sort.h
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include<stdlib.h>
#include<time.h>
//打印
void PrintArr(int* arr, int n);
//希尔排序
void ShellSort(int* arr, int n);
Sort.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"Sort.h"
//打印
void PrintArr(int* arr, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
//希尔排序时间复杂度:O(n^1.3)
void ShellSort(int* arr, int n)
{
int gap = n;//6
while (gap > 1)
{
gap = gap / 3 + 1;//保证最后一次gap一定为1
for (int i = 0; i < n - gap; i++)// i < n - gap是为了防止下面的tmp访问数组元素越界
{
int end = i;//n - gap - 1
int tmp = arr[end + gap];//n - 1
while (end >= 0)
{
if (arr[end] > tmp)
{
arr[end + gap] = arr[end];
end -= gap;
}
else {
break;
}
}
//也就是arr[end] = tmp;
arr[end + gap] = tmp;
}
}
}
test.c
int main()
{
int a[] = { 5, 3, 9, 6, 2, 4, 7, 1, 8 };
int n = sizeof(a) / sizeof(int);
printf("排序前:");
PrintArr(a, n);
ShellSort(a,n);
printf("排序后:");
PrintArr(a, n);
return 0;
}
希尔排序的时间复杂度计算
希尔排序的时间复杂度估算:
外层循环:
外层循环的时间复杂度可以直接给出为:O(log2n) 或者O(log3n) ,即O(log n)
内层循环:


通过以上的分析,可以画出这样的曲线图:
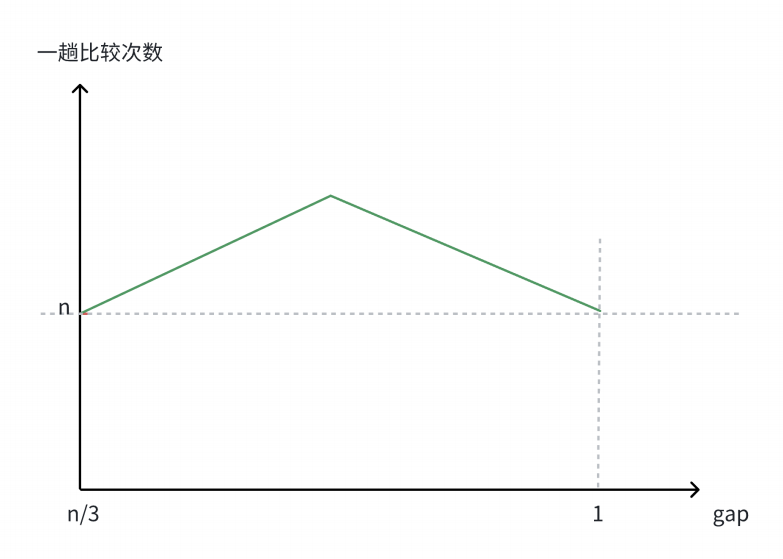
因此,希尔排序在最初和最后的排序的次数都为n,即前一阶段排序次数是逐渐上升的状态,当到达某一顶点时,排序次数逐渐下降至n,而该顶点的计算暂时无法给出具体的计算过程。
希尔排序时间复杂度不好计算,因为 gap 的取值很多,导致很难去计算,因此很多书中给出的希尔排序的时间复杂度都不固定。《数据结构(C语言版)》— 严蔚敏书中给出的时间复杂度为:




















