蚁群算法
1.蚁群算法来源
蚁群算法(Ant Colony Optimization,简称ACO)是一种模拟自然界中蚂蚁寻找食物路径行为的优化算法,主要用于解决组合优化问题。它的灵感来源于意大利学者Marco Dorigo在1992年提出的蚂蚁系统模型。

蚁群算法的灵感来源于自然界中蚂蚁寻找食物的行为。蚂蚁在寻找食物的过程中会释放一种称为信息素的化学物质,这种物质会在蚂蚁走过的路径上留下痕迹,后续的蚂蚁会根据这些信息素的浓度来选择路径,从而形成一条从蚁巢到食物源的最短路径。蚂蚁觅食的过程是一个正反馈的过程,该路段经过的蚂蚁越多,信息素留下的就越多,浓度越高,更多的蚂蚁都会选择这个路段。
这种行为模式启发了科学家们设计出蚁群算法,用于解决复杂的优化问题。
2.蚁群算法基本原理

蚁群算法的基本原理可以概括为以下几个步骤:
(1)初始化:设定每个解(相当于蚂蚁可能行走的路径)的信息素初始值,通常设置为一个较小的正数。
(2)蚂蚁构建解:每只蚂蚁根据当前的信息素浓度和启发式信息(如距离的倒数)来选择下一步要走的路径。这个过程是概率性的,信息素浓度越高,被选中的概率越大。
(3)信息素更新:一轮搜索结束后,根据蚂蚁找到的解的质量来更新信息素。通常情况下,较优的解对应的路径上的信息素会被加强,而较差解对应的信息素则会减少或蒸发。
(4)循环迭代:重复上述过程,直到满足停止条件(如达到最大迭代次数或解的质量不再明显提高)。
通过这样的机制,蚁群算法能够在解空间中逐渐逼近最优解。需要注意的是,蚁群算法是一种随机优化算法,每次运行可能会得到不同的结果,但多次运行后往往能够找到接近最优的解。
数学原理:

3.蚁群算法的应用
蚁群算法的应用非常广泛,包括旅行商问题(TSP)、图着色问题、网络路由优化、调度问题等。它特别适合于解决大规模的、复杂的优化问题,尤其是那些难以用传统数学方法求解的问题。
下面简单介绍一些经典的应用:
(1)旅行商问题(TSP):最初被用于解决TSP问题,即在给定一组城市中找到最短的巡回路径。

(2)物流和交通:用于优化物流配送路径、车辆路径规划和交通信号控制等问题。
**(3)网络路由:**在计算机网络和通信网络中,用于动态路由选择以提高网络效率。
**(4)生产调度:**在制造业中,用于优化生产计划和调度,减少生产成本和时间。
**(5)图像处理:**用于图像分割、边缘检测等图像处理任务。
(6)图着色问题:

4.蚁群算法解决TSP问题
旅行商问题(Traveling saleman problem, TSP)是物流配送的典型问题,其求解有十分重要的理论和现实意义。
旅行商问题传统的解决方法都是遗传算法,但是遗传算法的收敛速度慢,具有一定的缺陷。
在求解TSP蚁群算法中,每只蚂蚁相互独立,用于构造不同的路线,蚂蚁之间通过信息素进行交流,合作求解。
动图展示TSP问题求解过程:

下面介绍一下具体流程:
(1)初始化参数:epochs表示迭代次数,ants表示蚂蚁数量,alpha和beta是信息素重要程度的参数,rho是信息素挥发速度,Q是信息素强度常数。
(2)计算城市之间的距离矩阵:使用numpy的linalg.norm函数计算每对城市之间的欧几里得距离,并将结果存储在Distance矩阵中。
(3)初始化信息素矩阵Tau:将所有元素设置为1.0。
(4)初始化每只蚂蚁的路线图Route:创建一个ants x cities的零矩阵,表示每只蚂蚁访问过的城市。
(5)进行迭代:对于每次迭代,首先为每只蚂蚁随机选择一个起始城市,然后根据概率选择下一个要访问的城市。概率由信息素浓度和启发式信息共同决定。
(6)计算每只蚂蚁的总距离:遍历每只蚂蚁的路线,累加经过的城市之间的距离。
(7)更新最优解:如果当前迭代中找到了一条更短的路径,就更新最优距离和最优路线。
(8)更新信息素:根据蚂蚁走过的路径,更新信息素矩阵Tau。
(9)输出结果:打印出找到的最短路径和对应的距离。
程序中各符号说明如下表格:
| 变量/矩阵名称 | 维度 | 描述 |
|---|---|---|
| position | (cities, 2) | 城市坐标数组,每行代表一个城市的x和y坐标。 |
| Distance | (cities, cities) | 城市之间的距离矩阵,存储每两个城市之间的欧几里得距离。 |
| Eta | (cities, cities) | 启发式信息矩阵,是Distance矩阵的倒数,用于指导蚂蚁选择路径。 |
| Tau | (cities, cities) | 信息素矩阵,表示在每两个城市之间的路径上的信息素浓度。 |
| Route | (ants, cities) | 蚂蚁路径矩阵,存储每一只蚂蚁在当前迭代中的路径。 |
| best_distance | 1 | 变量,存储迄今为止找到的最短路径的长度。 |
| best_route | (cities,) | 数组,存储迄今为止找到的最短路径的城市顺序。 |
| epochs | 1 | 算法运行的迭代次数。 |
| ants | 1 | 蚁群中蚂蚁的数量。 |
| alpha | 1 | 信息素重要性的影响因子。 |
| beta | 1 | 启发式信息重要性的影响因子。 |
| rho | 1 | 信息素蒸发率。 |
| Q | 1 | 信息素强度,用于在每次迭代后更新信息素矩阵。 |
最终结果展示:


完整python代码如下:
import numpy as np
import random
# 城市坐标
x = np.array([51, 27, 56, 21, 4, 6, 58, 71, 54, 40, 94, 18, 89, 33, 12, 25, 24, 58, 71, 94, 17, 38, 13, 82, 12, 58, 45, 11, 47, 4])
y = np.array([14, 81, 67, 92, 64, 19, 98, 18, 62, 69, 30, 54, 10, 46, 34, 18, 42, 69, 61, 78, 16, 40, 10, 7, 32, 17, 21, 26, 35, 90])
position = np.column_stack((x, y))
epochs = 50
ants = 50
alpha = 1.4
beta = 2.2
rho = 0.15
Q = 10**6
cities = position.shape[0]
# 城市之间的距离矩阵
Distance = np.ones((cities, cities))
for i in range(cities):
for j in range(cities):
if i != j:
Distance[i, j] = np.linalg.norm(position[i] - position[j])
else:
Distance[i, j] = np.finfo(float).eps
Eta = 1.0 / Distance
Tau = np.ones((cities, cities))
# 每只蚂蚁的路线图
Route = np.zeros((ants, cities))
best_distance = np.inf
best_route = np.zeros(cities)
for epoch in range(epochs):
# 为每只蚂蚁随机选择一个唯一的起始城市
start_cities = np.random.permutation(cities).tolist()
for i in range(ants):
Route[i, 0] = start_cities[i % cities]
for j in range(1, cities):
for i in range(ants):
Visited = Route[i, :j]
NoVisited = np.setdiff1d(np.arange(cities), Visited)
P = np.zeros(len(NoVisited))
for k in range(len(NoVisited)):
P[k] = (Tau[int(Visited[-1]), int(NoVisited[k])] ** alpha) * (Eta[int(Visited[-1]), int(NoVisited[k])] ** beta)
P = P / P.sum()
Pcum = np.cumsum(P)
select = np.where(Pcum >= random.random())[0][0]
to_visit = NoVisited[select]
Route[i, j] = to_visit
Distance_epoch = np.zeros(ants)
for i in range(ants):
R = Route[i, :]
for j in range(cities - 1):
Distance_epoch[i] += Distance[int(R[j]), int(R[j + 1])]
Distance_epoch[i] += Distance[int(R[0]), int(R[-1])]
best_distance_epoch = np.min(Distance_epoch)
best_index_epoch = np.argmin(Distance_epoch)
if best_distance_epoch < best_distance:
best_distance = best_distance_epoch
best_route = Route[best_index_epoch, :]
Delta_Tau = np.zeros((cities, cities))
for i in range(ants):
for j in range(cities - 1):
Delta_Tau[int(Route[i, j]), int(Route[i, j + 1])] += Q / Distance_epoch[i]
Delta_Tau[int(Route[i, 0]), int(Route[i, -1])] += Q / Distance_epoch[i]
Tau = (1 - rho) * Tau + Delta_Tau
print("最短路径:", best_route)
print("最短距离:", best_distance)
MATLAB代码如下:
动图显示路径部分
function DrawRoute(C, R)
N = length(R);
scatter(C(:, 1), C(:, 2));
hold on
plot([C(R(1), 1), C(R(N), 1)], [C(R(1), 2), C(R(N), 2)], 'g');
for ii = 2: N
hold on
plot([C(R(ii - 1), 1), C(R(ii), 1)], [C(R(ii - 1), 2), C(R(ii), 2)], 'g');
pause(0.1)
frame = getframe(gcf);
imind = frame2im(frame);
[imind, cm] = rgb2ind(imind, 256);
if ii == 2
imwrite(imind, cm, 'test.gif', 'gif', 'Loopcount', inf, 'DelayTime', 1e-4);
else
imwrite(imind, cm, 'test.gif', 'gif', 'WriteMode', 'append', 'DelayTime', 1e-4);
end
end
title('旅行商规划');
蚁群算法部分:
clear;
clc;
x=[51 27 56 21 4 6 58 71 54 40 94 18 89 33 12 25 24 58 71 94 17 38 13 82 12 58 45 11 47 4]';
y=[14 81 67 92 64 19 98 18 62 69 30 54 10 46 34 18 42 69 61 78 16 40 10 7 32 17 21 26 35 90]';
position = 100 * randn(40, 2);
% position = [x, y];
epochs = 50;
ants = 50;
alpha = 1.4;
beta = 2.2;
rho = 0.15;Q = 10^6;
cities = size(position, 1);
% 城市之间的距离矩阵
Distance = ones(cities, cities);
for i = 1: cities
for j = 1: cities
if i ~= j
Distance(i, j) = ((position(i, 1) - position(j, 1))^2 + (position(i, 2) - position(j, 2))^2)^0.5;
else
Distance(i, j) = eps;
end
Distance(j, i) = Distance(i, j);
end
end
Eta = 1./Distance;
Tau = ones(cities, cities);
% 每只蚂蚁的路线图
Route = zeros(ants, cities);
epoch = 1;
% 记录每回合最优城市
R_best = zeros(epochs, cities);
L_best = inf .* ones(epochs, 1);
L_ave = zeros(epochs, 1);
% 开始迭代
while epoch <= epochs
% 随机位置
RandPos = [];
for i = 1: ceil(ants / cities)
RandPos = [RandPos, randperm(cities)];
end
Route(:, 1) = (RandPos(1, 1:ants))';
for j = 2:cities
for i = 1: ants
Visited = Route(i, 1:j-1);
NoVisited = zeros(1, (cities - j + 1));
P = NoVisited;
num = 1;
for k = 1: cities
if length(find(Visited == k)) == 0
NoVisited(num) = k;
num = num + 1;
end
end
for k = 1: length(NoVisited)
P(k) = (Tau(Visited(end), NoVisited(k))^alpha) * (Eta(Visited(end), NoVisited(k))^beta);
end
P = P / sum(P);
Pcum = cumsum(P);
select = find(Pcum >= rand);
to_visit = NoVisited(select(1));
Route(i, j) = to_visit;
end
end
if epoch >= 2
Route(1, :) = R_best(epoch - 1, :);
end
Distance_epoch = zeros(ants, 1);
for i = 1: ants
R = Route(i, :);
for j = 1: cities - 1
Distance_epoch(i) = Distance_epoch(i) + Distance(R(j), R(j + 1));
end
Distance_epoch(i) = Distance_epoch(i) + Distance(R(1), R(cities));
end
L_best(epoch) = min(Distance_epoch);
pos = find(Distance_epoch == L_best(epoch));
R_best(epoch, :) = Route(pos(1), :);
L_ave(epoch) = mean(Distance_epoch);
epoch = epoch + 1;
Delta_Tau = zeros(cities, cities);
for i = 1: ants
for j = 1: (cities - 1)
Delta_Tau(Route(i, j), Route(i, j + 1)) = Delta_Tau(Route(i, j), Route(i, j + 1)) + Q / Distance_epoch(i);
end
Delta_Tau(Route(i, 1), Route(i, cities)) = Delta_Tau(Route(i, 1), Route(i, cities)) + Q / Distance_epoch(i);
end
Tau = (1 - rho) .* Tau + Delta_Tau;
Route = zeros(ants, cities);
end
%% 结果展示
Pos = find(L_best == min(L_best));
Short_Route = R_best(Pos(1), :);
Short_Length = L_best(Pos(1), :);
figure
% subplot(121);
DrawRoute(position, Short_Route);
% subplot(122);
% plot(L_best);
% hold on
% plot(L_ave, 'r');
% title('平均距离和最短距离');
蚁群算法解决TSP问题(c++)
#include<iostream>
#include<stdio.h>
#include<string>
#include<string.h>
#include<cmath>
#include<ctime>
#include<stdlib.h>
using namespace std;
int seed=(int)time(0);//产生随机种子
int CityPos[30][2]= {{87,7},{91,38},{83,46},{71,44},{64,60},{68,58},{83,69},{87,76},{74,78},{71,71},{58,69},{54,62},{51,67},{37,84},{41,94},{2,99},{7,64},{22,60},{25,62},{18,54},{4,50},{13,40},{18,40},{24,42},{25,38},{41,26},{45,21},{44,35},{58,35},{62,32}};
#define CITY_NUM 30//城市数量
#define ANT_NUM 30//蚁群数量
#define TMAC 10000//迭代最大次数
#define ROU 0.5//误差大小
#define ALPHA 1//信息素重要程度的参数
#define BETA 4//启发式因子重要程度的参数
#define Q 100//信息素残留参数
#define maxn 100
#define inf 0x3f3f3f3f
double dis[maxn][maxn];//距离矩阵
double info[maxn][maxn];//信息素矩阵
bool vis[CITY_NUM][CITY_NUM];//标记矩阵
//返回指定范围内的随机整数
int rnd(int low,int upper)
{
return low+(upper-low)*rand()/(RAND_MAX+1);
}
//返回指定范围内的随机浮点数
double rnd(double low,double upper)
{
double temp=rand()/((double)RAND_MAX+1.0);
return low+temp*(upper-low);
}
struct Ant
{
int path[CITY_NUM];//保存蚂蚁走的路径
double length;//路径总长度
bool vis[CITY_NUM];//标记走过的城市
int cur_cityno;//当前城市
int moved_cnt;//已走城市数量
//初始化
void Init()
{
memset(vis,false,sizeof(vis));
length=0;
cur_cityno=rnd(0,CITY_NUM);
path[0]=cur_cityno;
vis[cur_cityno]=true;
moved_cnt=1;
}
//选择下一个城市
int Choose()
{
int select_city=-1;//所选城市编号
double sum=0;
double prob[CITY_NUM];//保存每个城市被选中的概率
for(int i=0; i<CITY_NUM; i++)
{
if(!vis[i])
{
prob[i]=pow(info[cur_cityno][i],ALPHA)*pow(1.0/dis[cur_cityno][i], BETA);
sum=sum+prob[i];
}
else
{
prob[i]=0;
}
}
//进行轮盘选择
double temp=0;
if(sum>0)//总的信息素大于0
{
temp=rnd(0.0,sum);
for(int i=0; i<CITY_NUM; i++)
{
if(!vis[i])
{
temp=temp-prob[i];
if(temp<0.0)
{
select_city=i;
break;
}
}
}
}
else //信息素太少就随便找个没走过的城市
{
for(int i=0; i<CITY_NUM; i++)
{
if(!vis[i])
{
select_city=i;
break;
}
}
}
return select_city;
}
//蚂蚁的移动
void Move()
{
int nex_cityno=Choose();
path[moved_cnt]=nex_cityno;
vis[nex_cityno]=true;
length=length+dis[cur_cityno][nex_cityno];
cur_cityno=nex_cityno;
moved_cnt++;
}
//蚂蚁进行一次迭代
void Search()
{
Init();
while(moved_cnt<CITY_NUM)
{
Move();
}
//回到原来的城市
length=length+dis[path[CITY_NUM-1]][path[0]];
}
};
struct TSP
{
Ant ants[ANT_NUM];//定义蚁群
Ant ant_best;//最优路径蚂蚁
void Init()
{
//初始化为最大值
ant_best.length = inf;
//计算两两城市间距离
for (int i = 0; i < CITY_NUM; i++)
{
for (int j = 0; j < CITY_NUM; j++)
{
info[i][j]=1.0;
double temp1=CityPos[j][0]-CityPos[i][0];
double temp2=CityPos[j][1]-CityPos[i][1];
dis[i][j] = sqrt(temp1*temp1+temp2*temp2);
}
}
}
//更新信息素
void UpdateInfo()
{
double temp_info[CITY_NUM][CITY_NUM];
memset(temp_info,0,sizeof(temp_info));
int u,v;
for(int i=0; i<ANT_NUM; i++) //遍历每一只蚂蚁
{
for(int j=1; j<CITY_NUM; j++)
{
u=ants[i].path[j-1];
v=ants[i].path[j];
temp_info[u][v]=temp_info[u][v]+Q/ants[i].length;
temp_info[v][u]=temp_info[u][v];
}
//最后城市和开始城市之间的信息素
u=ants[i].path[0];
temp_info[u][v]=temp_info[u][v]+Q/ants[i].length;
temp_info[v][u]=temp_info[u][v];
}
for(int i=0; i<CITY_NUM; i++)
{
for(int j=0; j<CITY_NUM; j++)
{
info[i][j]=info[i][j]*ROU+temp_info[i][j];
}
}
}
void Search()
{
//迭代TMAC次
for(int i=0; i<TMAC; i++)
{
//所有蚂蚁都进行一次遍历
for(int j=0; j<ANT_NUM; j++)
{
ants[j].Search();
}
//保存所有蚂蚁遍历的最佳结果
for(int j=0; j<ANT_NUM; j++)
{
if(ant_best.length>ants[j].length)
{
ant_best=ants[j];
}
}
UpdateInfo();
printf("第%d次迭代最优路径长度是%lf\n", i,ant_best.length);
printf("\n");
}
}
};
int main()
{
srand(seed);
TSP tsp;
tsp.Init();
tsp.Search();
printf("最短路径如下\n");
for(int i=0;i<CITY_NUM;i++)
{
printf("%d",tsp.ant_best.path[i]);
if(i<CITY_NUM-1)
printf("->");
else
printf("\n");
}
return 0;
}
ACO算法在迭代构造解的过程之中应用到的信息包括以下两个方面:1) 算例的启发式信息(如路径问题中的距离);2) 反应蚂蚁路径搜索轨迹的信息素。
ACO中蚂蚁的行为细节
给定一个图网络 G=(C,L),其中 C表示图的组成成分(节点),L表示图的边。在执行ACO算法构造解的过程中,可以使用**“hard way”来构造的解,所有的解均不可以违反约束,也可以使用“soft way”**来构造解,某些解可以违反某些约束,但是这种解需要根据违反约束的程度来添加惩罚项(penalization)。
定义信息素 τ \tau τ若信息素和网络中的节点相关联, τij若信息素和网络中的边相关联;启发式信息 ηi若和节点相关联, ηij若和边相关联)。在ACO中,系统之中的每一个蚂蚁 k具有以下特点:
1)它通过探索网络 G=(C,L)来构造费用最小的解方案;
2)每一个蚂蚁k会有一个记录自己访问过路基的记忆 Mk,这个记忆信息可以用来继续构造可行解,来评判已经得到的解的优劣和更新信息素。
3)当蚂蚁 k k k在状态 xr=<xr−1,i>将要向节点 j ∈ N i k移动时 Nik表示蚂蚁 k在节点 i时的可行邻域),产生的新的状态 <xr,j>可以可行或者不可行。
4)每一个蚂蚁通过概率选择函数来选择移动方向,其中概率选择函数中包含的信息有:信息素,启发式信息,蚂蚁当前记忆信息和问题约束信息。
5)当终止条件满足时,终止蚂蚁的解方案构建。若不允许产生不可行解方案,则当构造不可行时,停止构造。
6)“步进信息素更新”(step-by-step pheromone update),表示每一次添加新的节点到某个蚂蚁的解之中,都需要对这个蚂蚁的信息素进行更新。
7)“在线延迟信息素更新”(online delayed pheromone update),表示在一个解方案构造完毕之后,在回溯整个解方案进行信息素的更新。
ACO构造解的过程
一个蚁群之中的蚂蚁并发地向网络 G G G中的邻域状态进行拓展来分别构造各自的路径,他们移动的方向收到概率选择函数的指导,通过不断的移动,每一个蚂蚁都向着构造组合优化问题的解方向靠近。一旦某个蚂蚁构造成功一个解方案,这个蚂蚁评估构造的解方案的优劣并进行信息素的更新。更新完毕的信息素又会通过概率选择函数指导后续蚂蚁的解方案构造过程。
信息素的消失和维持
信息素的消失(evaporation) 是将之前蚂蚁更新的信息素随着迭代次数的增加逐渐减小的过程。信息素的消失可以有效避免解太快收敛到一个局部最优解,同时可以帮助探索新的求解空间。
信息素维持(daemon) 可以帮助提高算法局部寻优的效果,在实际操作中,可以通过选择当前解方案最优的解,将当前最优解的信息素的更新占比加大,来提高最优解对于后续寻优的影响,这个过程也称为“离线信息素更新机制”off-line pheromone update。
ACO算法的改进方法
4.1 精英策略-elitist strategy
精英策略的思想在于基于当前最优解额外的信息素更新权重,在每一次信息素更新时,对于当前全局最优解中包含的弧给与额外的信息素权重,通过系数e来实现。应用了精英策略的上式(3)变为如下所示的形式:

其中 Lgb表示当前最优解的路径长度(成本)。
4.2 等级蚂蚁体系-rank-based version of Ant System( ASrank)
ASrank是精英策略的一种拓展策略,在ACO的所有解构造完成之后,将所有的解按照成本大小从小到大进行排序,值选择前 w−1个解方案和当前最优解方案进行信息素的更新。第 r个蚂蚁的解方案对于信息素更新的权重取值为:max{0, w−r},当前最优解对于信息素更新的权重取值为: w。在 ASrank下的上式(2)的表示形式如下所示:
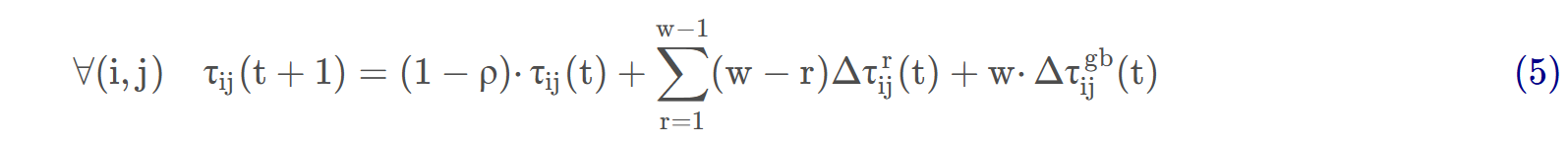
其中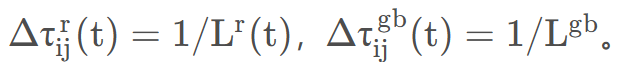
4.3 信息素重置
当连续一定迭代次数没有对当前解进行优化,或者总迭代次数达到一定的次数时,可以将信息素重置为初始化水平,从而达到改变求解空间的效果。
4.4 ACO和LS结合
在进行ACO的过程之中可以嵌入LS算法来局部优化每一个蚂蚁找到的解方案,同时优化之后的解方案被用来进行信息素的更新操作。
4.5 候选列表-candidate lists
当求解问题的邻域空间较大时,蚁群之中的蚂蚁很可能不在同一个求解空间之中,使得ACO的求解效率大大降低。为了弥补这一缺陷,可以使用候选列表的方式。对于VRPTW问题,在实际操作中,对于每一个客户点i,其候选列表包含 cl个与之距离最近的客户点,在构建解方案的过程中,首先选择候选列表中的客户点进行解方案的构建,之后再从其余客户点中选择客户点进行解方案的构建。
ACO求解VRPTW代码已上传值GitHub
https://github.com/Dragon-wang-fei-long/Huristic-code/tree/Dragon-wang-fei-long-ACO
参考文章:蚁群算法(Ant Colony Optimization,ACO)讲解+代码实现_蚁群算法的实现-CSDN博客
蚁群算法(ACO)原理梳理及应用细节 - 附求解VRPTW c++代码-阿里云开发者社区 (aliyun.com)