时间序列预测是分析和预测一系列时间顺序数据的方法。不同的时间序列预测方法在应用中根据数据特征和目标有不同的适用性。以下是时间序列预测方法的详细总结,包括概念、原理和Python实现代码。
1. 简单平均法 (Simple Average Method)
概念与原理: 简单平均法是最简单的时间序列预测方法,计算整个时间序列数据的平均值并将其作为所有未来时刻的预测值。这种方法假设时间序列的未来行为与过去的平均值一致。
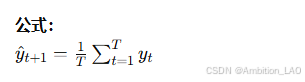
Python 实现:
import numpy as np def simple_average(series): return np.mean(series) # 示例数据 data = [3, 8, 12, 14, 18, 24, 27, 30, 31] prediction = simple_average(data) print(prediction)
2. 移动平均法 (Moving Average Method)
概念与原理: 移动平均法通过计算一段时间窗口内的平均值来平滑数据。适合处理波动性较大的时间序列数据。可以用于短期预测。
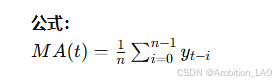
Python 实现:
import pandas as pd def moving_average(series, window): return series.rolling(window=window).mean() # 示例数据 data = pd.Series([3, 8, 12, 14, 18, 24, 27, 30, 31]) window = 3 ma = moving_average(data, window) print(ma)
3. 加权移动平均法 (Weighted Moving Average)
概念与原理: 加权移动平均法类似于移动平均法,但对不同时间点赋予不同的权重,通常是近期数据权重较大,远期数据权重较小。
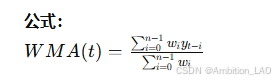
Python 实现:
import numpy as np def weighted_moving_average(series, weights): return np.convolve(series, weights[::-1], 'valid') / sum(weights) # 示例数据 data = [3, 8, 12, 14, 18, 24, 27, 30, 31] weights = [0.1, 0.3, 0.6] # 权重和为1 wma = weighted_moving_average(data, weights) print(wma)
4. 指数平滑法 (Exponential Smoothing)
概念与原理: 指数平滑法是移动平均法的一种扩展,较新的数据点赋予较大的权重,较旧的数据点权重逐渐减小。适合平稳时间序列的预测。
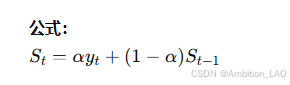
Python 实现:
def exponential_smoothing(series, alpha): result = [series[0]] # 第一个值保持不变 for n in range(1, len(series)): result.append(alpha * series[n] + (1 - alpha) * result[n-1]) return result # 示例数据 data = [3, 8, 12, 14, 18, 24, 27, 30, 31] alpha = 0.3 es = exponential_smoothing(data, alpha) print(es)
5. 双指数平滑法 (Double Exponential Smoothing)
概念与原理: 双指数平滑法适用于带有趋势的时间序列,它结合了水平和平滑趋势两个成分来进行预测。
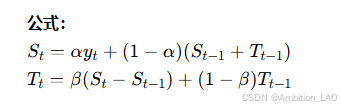
Python 实现:
def double_exponential_smoothing(series, alpha, beta): result = [series[0]] level, trend = series[0], series[1] - series[0] for n in range(1, len(series)): last_level, level = level, alpha * series[n] + (1 - alpha) * (level + trend) trend = beta * (level - last_level) + (1 - beta) * trend result.append(level + trend) return result # 示例数据 data = [3, 8, 12, 14, 18, 24, 27, 30, 31] alpha, beta = 0.5, 0.5 des = double_exponential_smoothing(data, alpha, beta) print(des)
6. 三指数平滑法 (Triple Exponential Smoothing/Holt-Winters)
概念与原理: 三指数平滑法,也称为 Holt-Winters 模型,适用于具有季节性变化的时间序列。它包含水平、趋势和季节性三个成分。
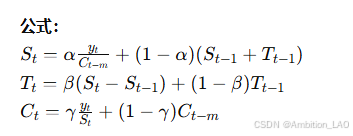
Python 实现:
import pandas as pd from statsmodels.tsa.holtwinters import ExponentialSmoothing # 示例数据 data = pd.Series([3, 8, 12, 14, 18, 24, 27, 30, 31]) model = ExponentialSmoothing(data, seasonal='add', seasonal_periods=4) model_fit = model.fit() predictions = model_fit.predict(start=len(data), end=len(data)+4) print(predictions)
7. 自回归模型 (AR, AutoRegressive Model)
概念与原理: 自回归模型假设时间序列的当前值是过去若干时间点值的线性组合。适用于平稳时间序列。
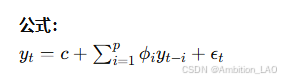
Python 实现:
from statsmodels.tsa.ar_model import AutoReg # 示例数据 data = pd.Series([3, 8, 12, 14, 18, 24, 27, 30, 31]) model = AutoReg(data, lags=1) model_fit = model.fit() predictions = model_fit.predict(start=len(data), end=len(data)+4) print(predictions)
8. 移动平均模型 (MA, Moving Average Model)
概念与原理: 移动平均模型假设时间序列的当前值是过去若干误差项的线性组合。适用于平稳时间序列。
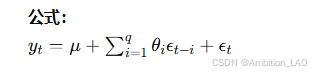
Python 实现:
from statsmodels.tsa.arima.model import ARIMA # 示例数据 data = pd.Series([3, 8, 12, 14, 18, 24, 27, 30, 31]) model = ARIMA(data, order=(0, 0, 1)) model_fit = model.fit() predictions = model_fit.predict(start=len(data), end=len(data)+4) print(predictions)
9. 自回归移动平均模型 (ARMA)
概念与原理: ARMA 模型结合了自回归和移动平均两个模型,适用于平稳时间序列的建模。
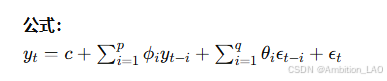
Python 实现:
from statsmodels.tsa.arima.model import ARIMA # 示例数据 data = pd.Series([3, 8, 12, 14, 18, 24, 27, 30, 31]) model = ARIMA(data, order=(2, 0, 1)) model_fit = model.fit() predictions = model_fit.predict(start=len(data), end=len(data)+4) print(predictions)
10. 自回归积分移动平均模型 (ARIMA)
概念与原理: ARIMA 模型适用于非平稳时间序列,通过差分的方法使得时间序列平稳,再应用 ARMA 模型进行预测。
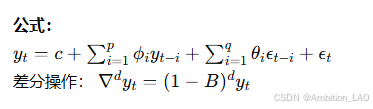
Python 实现:
from statsmodels.tsa.arima.model import ARIMA # 示例数据 data = pd.Series([3, 8, 12, 14, 18, 24, 27, 30, 31]) model = ARIMA(data, order=(2, 1, 1)) model_fit = model.fit() predictions = model_fit.predict(start=len(data), end=len(data)+4) print(predictions)
11. 季节性自回归积分移动平均模型 (SARIMA)
概念与原理: SARIMA 模型扩展了 ARIMA 模型,加入了季节性成分,适用于具有季节性模式的时间序列。
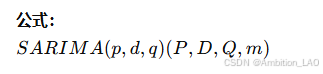
Python 实现:
from statsmodels.tsa.statespace.sarimax import SARIMAX # 示例数据 data = pd.Series([3, 8, 12, 14, 18, 24, 27, 30, 31]) model = SARIMAX(data, order=(1, 1, 1), seasonal_order=(1, 1, 1, 12)) model_fit = model.fit() predictions = model_fit.predict(start=len(data), end=len(data)+4) print(predictions)
12. 自回归条件异方差模型 (ARCH)
概念与原理: ARCH 模型用于建模和预测时间序列中的波动性,通过自回归条件异方差来描述时间序列方差的动态变化。
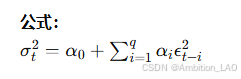
Python 实现:
from arch import arch_model # 示例数据 data = pd.Series([3, 8, 12, 14, 18, 24, 27, 30, 31]) model = arch_model(data, vol='ARCH', p=1) model_fit = model.fit() predictions = model_fit.forecast(horizon=5) print(predictions.variance.values[-1:])
13. 广义自回归条件异方差模型 (GARCH)
概念与原理: GARCH 模型是 ARCH 模型的扩展,适用于更复杂的时间序列波动性建模。它将误差项的平方和过去波动率结合起来进行预测。
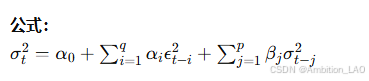
Python 实现:
from arch import arch_model # 示例数据 data = pd.Series([3, 8, 12, 14, 18, 24, 27, 30, 31]) model = arch_model(data, vol='GARCH', p=1, q=1) model_fit = model.fit() predictions = model_fit.forecast(horizon=5) print(predictions.variance.values[-1:])
14. 长短期记忆网络 (LSTM, Long Short-Term Memory)
概念与原理: LSTM 是一种特殊的循环神经网络(RNN),在时间序列预测中特别有效,能够捕捉时间序列中的长时间依赖关系。
Python 实现:
import numpy as np import pandas as pd from keras.models import Sequential from keras.layers import LSTM, Dense from sklearn.preprocessing import MinMaxScaler # 准备数据 data = np.array([3, 8, 12, 14, 18, 24, 27, 30, 31]) data = data.reshape(-1, 1) scaler = MinMaxScaler(feature_range=(0, 1)) data = scaler.fit_transform(data) # 构造输入和输出 X, y = [], [] for i in range(len(data)-3): X.append(data[i:i+3]) y.append(data[i+3]) X, y = np.array(X), np.array(y) # 构建模型 model = Sequential() model.add(LSTM(50, activation='relu', input_shape=(X.shape[1], X.shape[2]))) model.add(Dense(1)) model.compile(optimizer='adam', loss='mse') # 训练模型 model.fit(X, y, epochs=200, verbose=0) # 预测 x_input = data[-3:].reshape(1, 3, 1) prediction = model.predict(x_input, verbose=0) prediction = scaler.inverse_transform(prediction) print(prediction)
15. Prophet
概念与原理: Prophet 是由 Facebook 开发的时间序列预测模型,设计用于处理具有明确季节性和节假日影响的时间序列。它的优点是易于使用且适合处理大规模数据。
Python 实现:
from fbprophet import Prophet
import pandas as pd
# 示例数据
data = pd.DataFrame({
'ds': pd.date_range(start='2020-01-01', periods=9, freq='M'),
'y': [3, 8, 12, 14, 18, 24, 27, 30, 31]
})
model = Prophet()
model.fit(data)
# 预测
future = model.make_future_dataframe(periods=5, freq='M')
forecast = model.predict(future)
print(forecast[['ds', 'yhat', 'yhat_lower', 'yhat_upper']])
结论
以上介绍的时间序列预测方法涵盖了从简单的平均法、移动平均法到复杂的机器学习模型,如LSTM和Prophet。不同的方法适用于不同类型的时间序列数据,在实际应用中,通常需要对比多种方法的预测效果,选择最优的模型来进行预测。