1 简介
图是一种用 节点 和 边 来表示相互关系的数学模型,其中节点代表事物,边代表事物间的联系。图作为一种数据结构,在各种领域都有广泛应用,如社交网络、城市交通网络、互联网页面链接等。
图由两个主要部分构成:
节点(也称为顶点)和边。
节点代表图中的基本单元,可以是具有某种特性的实体,例如人、地点或其他对象。边则代表这些节点之间的关系或连接。
根据边的方向性,可以分为:
有向图和无向图。
无向图中的边没有方向,通常用来表示双向对称的关系;而有向图中的边有明确的方向,用以表示非对称的关系。
2 图解
2.1 分类
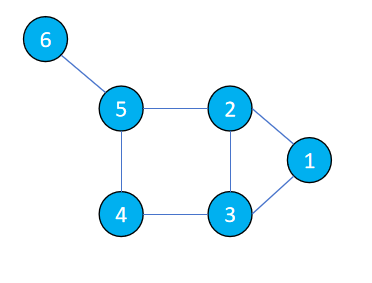
2.1.1 无向图
2.1.2 有向图

2.2 结构
2.2.1 邻接矩阵

- 无向图:在无向图中,邻接矩阵是对称的,矩阵中的每个元素[i][j]表示顶点i与顶点j之间是否存在边。如果是1,则存在边;如果是0,则不存在边。
- 有向图:在有向图中,有向图的邻接矩阵不一定对称。矩阵中的元素[i][j]表示从顶点i到顶点j是否有一个箭头。这实现了有向图的方向性特性。
- 带权图:当图的边被赋予权值时,这些权值可以代替邻接矩阵中的1,表示顶点间的距离或成本。如果两个顶点之间没有直接的边,则通常用一个很大的数来表示不可达
- 特点:邻接矩阵可以快速确定两个顶点之间是否存在边。然而,对于稀疏图来说,邻接矩阵可能浪费大量的存储空间,因为它存储了许多不存在的边的信息。
public class AdjacencyMatrix {
private int[][] matrix; // 邻接矩阵
private int numVertices; // 顶点数量
// 构造函数,初始化邻接矩阵和顶点数量
public AdjacencyMatrix(int numVertices) {
this.numVertices = numVertices;
matrix = new int[numVertices][numVertices];
}
// 添加一条边
public void addEdge(int i, int j) {
if (i >= 0 && i < numVertices && j >= 0 && j < numVertices) {
matrix[i][j] = 1; // 有向图
matrix[j][i] = 1; // 无向图
}
}
// 删除一条边
public void removeEdge(int i, int j) {
if (i >= 0 && i < numVertices && j >= 0 && j < numVertices) {
matrix[i][j] = 0; // 有向图
matrix[j][i] = 0; // 无向图
}
}
// 检查两个顶点之间是否存在边
public boolean hasEdge(int i, int j) {
if (i >= 0 && i < numVertices && j >= 0 && j < numVertices) {
return matrix[i][j] == 1;
}
return false;
}
// 打印邻接矩阵
public void printMatrix() {
for (int i = 0; i < numVertices; i++) {
for (int j = 0; j < numVertices; j++) {
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
}
public static void main(String[] args) {
AdjacencyMatrix graph = new AdjacencyMatrix(6);
graph.addEdge(6, 5);
graph.addEdge(5, 2);
graph.addEdge(2, 1);
graph.addEdge(5, 4);
graph.addEdge(4, 3);
graph.addEdge(2, 3);
graph.addEdge(1, 3);
graph.printMatrix();
}
}2.2.2 邻接表

- 无向图:在无向图的邻接表中,每个顶点都有一个与之关联的链表,记录了所有与其相邻的顶点。这种方法只存储存在的边,对稀疏图来说很有效。
- 有向图:对于有向图,邻接表记录每个顶点发出的边。有时为了方便获取顶点的入度,会额外建立一个逆邻接表来快速查找以某个顶点为终点的边。
- 带权图:带权值的网在邻接表中存储时,每条边除了要记录邻接顶点外,还要记录边的权值。这使得计算路径权重更加直接。
- 特点:邻接表适合表示稀疏图,节约存储空间。但是,相比于邻接矩阵,邻接表在判断两个顶点间是否存在边时效率较低。
public class AdjacencyList {
private List<List<Integer>> adjacencyList; // 邻接表
private int numVertices; // 顶点数量
// 构造函数,初始化邻接表和顶点数量
public AdjacencyList(int numVertices) {
this.numVertices = numVertices;
adjacencyList = new ArrayList<>(numVertices);
for (int i = 0; i < numVertices; i++) {
adjacencyList.add(new ArrayList<>());
}
}
// 添加一条边
public void addEdge(int i, int j) {
if (i >= 0 && i < numVertices && j >= 0 && j < numVertices) {
adjacencyList.get(i).add(j); // 有向图
adjacencyList.get(j).add(i); // 无向图
}
}
// 删除一条边
public void removeEdge(int i, int j) {
if (i >= 0 && i < numVertices && j >= 0 && j < numVertices) {
adjacencyList.get(i).remove((Integer) j); // 有向图
adjacencyList.get(j).remove((Integer) i); // 无向图
}
}
// 检查两个顶点之间是否存在边
public boolean hasEdge(int i, int j) {
if (i >= 0 && i < numVertices && j >= 0 && j < numVertices) {
return adjacencyList.get(i).contains(j);
}
return false;
}
// 打印邻接表
public void printAdjacencyList() {
for (int i = 0; i < numVertices; i++) {
System.out.print("Vertex " + i + ": ");
for (int j : adjacencyList.get(i)) {
System.out.print(j + " ");
}
System.out.println();
}
}
public static void main(String[] args) {
AdjacencyList graph = new AdjacencyList(6);
graph.addEdge(6, 5);
graph.addEdge(5, 2);
graph.addEdge(2, 1);
graph.addEdge(5, 4);
graph.addEdge(4, 3);
graph.addEdge(2, 3);
graph.addEdge(1, 3);
graph.printAdjacencyList();
}
}2.2.3 其他
还有一些用于特定的场景和需求,比如十字链表、邻接多重表和边集数组则等,知道即可,就不多赘述。
-
十字链表
十字链表结合了邻接表和逆邻接表的优点,使得在有向图中可以同时快速获取一个顶点的入度和出度信息。此外,它在一定程度上保持了邻接表的存储效率。 -
邻接多重表
邻接多重表对无向图的存储结构进行了优化,使得边的操作更加方便。与邻接表相比,每条边在邻接多重表中只由一个结点表示,而不是两个。 -
边集数组
边集数组强调的是边的集合,它使用两个一维数组,分别存储图中每个顶点的信息和边的信息。这种方法在需要对边进行依次处理时比较适用,但查找一个顶点的邻居需要扫描整个边数组,效率并不高。
4 总结
本章主要介绍了图的两种结构。在此对以上总结:
邻接矩阵:
- 表示方法:使用一个二维数组,其中行和列代表图中的顶点,矩阵中的元素表示顶点之间的边。
- 适用场景:适合于稠密图,即图中的边数量接近于顶点数量的平方。
- 优点:查询顶点之间是否存在边的时间复杂度为O(1)。
- 缺点:空间复杂度高,为O(V^2),其中V是顶点数量;更新图(添加或删除顶点和边)的成本较高。
邻接表:
- 表示方法:使用一个列表数组,每个顶点对应一个列表,列表中包含所有与该顶点相邻的顶点。
- 适用场景:适合于稀疏图,即图中的边数量远少于顶点数量的平方。
- 优点:空间复杂度低,为O(V+E),其中V是顶点数量,E是边数量;更新图的操作较为高效。
- 缺点:查询顶点之间是否存在边的时间复杂度为O(degree(v)),其中degree(v)是顶点v的度。
在选择图的存储结构时,需要考虑以下因素:
- 图的类型:有向图、无向图、加权图等。
- 图的密度:稀疏图还是稠密图。
- 操作类型:频繁执行的操作,如查找、插入、删除等。
- 空间和时间效率:根据应用场景选择合适的存储结构以优化性能。
总之,邻接矩阵和邻接表各有优劣,适用于不同的场景。在实际应用中,应根据具体需求和图的特性来选择最合适的存储结构。