代码随想录算法训练营

题目信息 654. 最大二叉树

题目链接: https://leetcode.cn/problems/maximum-binary-tree/
题目描述:
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值左边的 子数组前缀上 构建左子树。
递归地在最大值右边的 子数组后缀上 构建右子树。

返回 nums 构建的 最大二叉树 。

解法一: {{递归}}

解题思路

最大二叉树的构建过程如下：

654.最大二叉树

构造树一般采用的是前序遍历，因为先构造中间节点，然后递归构造左子树和右子树。

确定递归函数的参数和返回值

参数传入的是存放元素的数组，返回该数组构造的二叉树的头结点，返回类型是指向节点的指针。

代码如下：

public TreeNode constructMaximumBinaryTree(int[] nums)

确定终止条件

题目中说了输入的数组大小一定是大于等于1的，所以我们不用考虑小于1的情况，那么当递归遍历的时候，如果传入的数组大小为1，说明遍历到了叶子节点了。

那么应该定义一个新的节点，并把这个数组的数值赋给新的节点，然后返回这个节点。这表示一个数组大小是1的时候，构造了一个新的节点，并返回。

代码如下：

TreeNode node = new TreeNode(0);  
if (nums.length == 0){  
    node.val = nums[0];  
    return node;  
}

确定单层递归的逻辑

这里有三步工作

先要找到数组中最大的值和对应的下标，最大的值构造根节点，下标用来下一步分割数组。

代码如下：

// 找到数组中最大的值和对应的下标  
int maxValue = 0;  
int maxValueIndex = 0;  
for (int i = 0;i < nums.length;i++){  
    if (nums[i] > maxValue){  
        maxValue = nums[i];  
        maxValueIndex = i ;  
    }  
}  
node.val = maxValue;

最大值所在的下标左区间构造左子树

这里要判断maxValueIndex > 0，因为要保证左区间至少有一个数值。

代码如下：

// 最大值所在的下标左区间 构造左子树  
if (maxValueIndex > 0){  
    int [] newNums = Arrays.copyOfRange(nums,0,maxValueIndex);  
    node.left = constructMaximumBinaryTree(newNums);  
}

最大值所在的下标右区间构造右子树

判断maxValueIndex < (nums.size() - 1)，确保右区间至少有一个数值。

代码如下：

// 最大值所在的下标右区间 构造右子树  
if (maxValueIndex < (nums.length - 1)){  
    int [] newNums = Arrays.copyOfRange(nums,maxValueIndex + 1,nums.length);  
    node.right = constructMaximumBinaryTree(newNums);  
}

这样我们就分析完了，整体代码如下：（详细注释）

代码实现

public TreeNode constructMaximumBinaryTree(int[] nums) {  
    TreeNode node = new TreeNode(0);  
    if (nums.length == 0){  
        node.val = nums[0];  
        return node;  
    }  
    // 找到数组中最大的值和对应的下标  
    int maxValue = 0;  
    int maxValueIndex = 0;  
    for (int i = 0;i < nums.length;i++){  
        if (nums[i] > maxValue){  
            maxValue = nums[i];  
            maxValueIndex = i ;  
        }  
    }  
    node.val = maxValue;  
    // 最大值所在的下标左区间 构造左子树  
    if (maxValueIndex > 0){  
        int [] newNums = Arrays.copyOfRange(nums,0,maxValueIndex);  
        node.left = constructMaximumBinaryTree(newNums);  
    }  
    // 最大值所在的下标右区间 构造右子树  
    if (maxValueIndex < (nums.length - 1)){  
        int [] newNums = Arrays.copyOfRange(nums,maxValueIndex + 1,nums.length);  
        node.right = constructMaximumBinaryTree(newNums);  
    }  
    return node;  
  
}

解法二

代码实现

class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return constructMaximumBinaryTree1(nums, 0, nums.length);
    }

    public TreeNode constructMaximumBinaryTree1(int[] nums, int leftIndex, int rightIndex) {
        if (rightIndex - leftIndex < 1) {// 没有元素了
            return null;
        }
        if (rightIndex - leftIndex == 1) {// 只有一个元素
            return new TreeNode(nums[leftIndex]);
        }
        int maxIndex = leftIndex;// 最大值所在位置
        int maxVal = nums[maxIndex];// 最大值
        for (int i = leftIndex + 1; i < rightIndex; i++) {
            if (nums[i] > maxVal){
                maxVal = nums[i];
                maxIndex = i;
            }
        }
        TreeNode root = new TreeNode(maxVal);
        // 根据maxIndex划分左右子树
        root.left = constructMaximumBinaryTree1(nums, leftIndex, maxIndex);
        root.right = constructMaximumBinaryTree1(nums, maxIndex + 1, rightIndex);
        return root;
    }
}

题目信息 617. 合并二叉树

题目链接: https://leetcode.cn/problems/merge-two-binary-trees/description/
题目描述:
给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

解题思路

递归

二叉树使用递归，就要想使用前中后哪种遍历方式？

本题使用哪种遍历都是可以的！

我们下面以前序遍历为例。

动画如下：

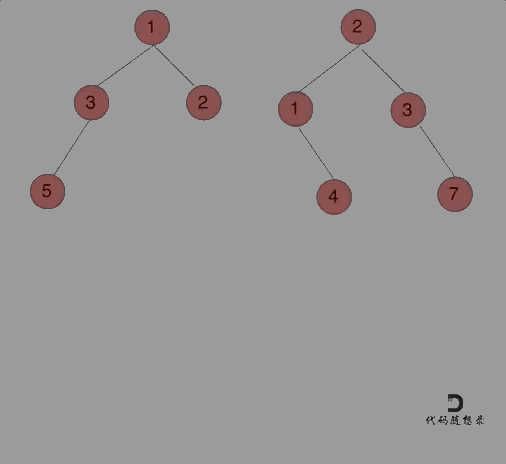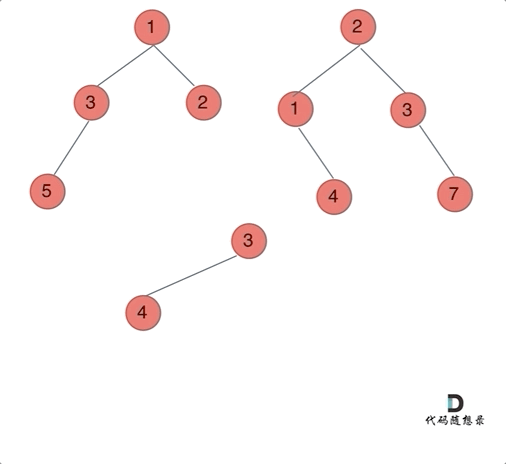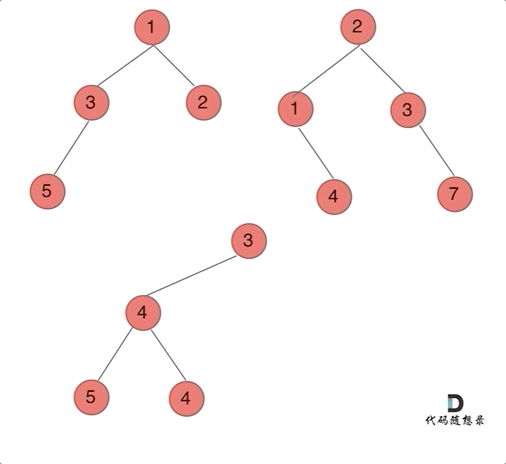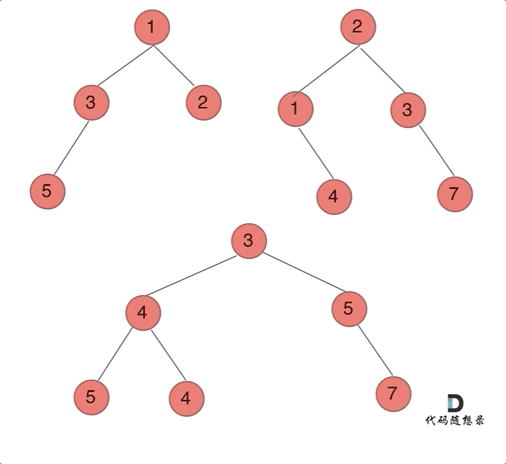
617.合并二叉树

那么我们来按照递归三部曲来解决：

确定递归函数的参数和返回值：

首先要合入两个二叉树，那么参数至少是要传入两个二叉树的根节点，返回值就是合并之后二叉树的根节点。

代码如下：

public TreeNode mergeTrees(TreeNode root1, TreeNode root2)

确定终止条件：

因为是传入了两个树，那么就有两个树遍历的节点t1 和 t2，如果t1 == NULL 了，两个树合并就应该是 t2 了（如果t2也为NULL也无所谓，合并之后就是NULL）。

反过来如果t2 == NULL，那么两个数合并就是t1（如果t1也为NULL也无所谓，合并之后就是NULL）。

代码如下：

if (root1 == null) return root2; // 如果t1为空，合并之后就应该是t2
if (root2 == null) return root1; // 如果t2为空，合并之后就应该是t1

确定单层递归的逻辑：

单层递归的逻辑就比较好写了，这里我们重复利用一下t1这个树，t1就是合并之后树的根节点（就是修改了原来树的结构）。

那么单层递归中，就要把两棵树的元素加到一起。

root1.val += root2.val;

接下来t1 的左子树是：合并 t1左子树 t2左子树之后的左子树。

t1 的右子树：是合并 t1右子树 t2右子树之后的右子树。

最终t1就是合并之后的根节点。

代码如下：

root1.left = mergeTrees(root1.left,root2.left);  
root1.right = mergeTrees(root1.right,root2.right);  
return root1;

此时前序遍历，完整代码就写出来了，如下：

代码实现

public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {  
    if (root1 == null) return root2;  
    if (root2 == null) return root1;  
  
    root1.val += root2.val;  
    root1.left = mergeTrees(root1.left,root2.left);  
    root1.right = mergeTrees(root1.right,root2.right);  
    return root1;  
}

题目信息 700. 二叉搜索树中的搜索

题目链接: https://leetcode.cn/problems/search-in-a-binary-search-tree/description/
题目描述:
给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。返回以该节点为根的子树。如果节点不存在，则返回 null 。

解法一: {{递归法}}

解题思路

递归法

确定递归函数的参数和返回值

递归函数的参数传入的就是根节点和要搜索的数值，返回的就是以这个搜索数值所在的节点。

代码如下：

public TreeNode searchBST(TreeNode root, int val)

确定终止条件

如果root为空，或者找到这个数值了，就返回root节点。

if (root == null || root.val == val)  return root;

确定单层递归的逻辑

看看二叉搜索树的单层递归逻辑有何不同。

因为二叉搜索树的节点是有序的，所以可以有方向的去搜索。

如果root->val > val，搜索左子树，如果root->val < val，就搜索右子树，最后如果都没有搜索到，就返回NULL。

代码如下：

TreeNode result = null;  
if (root.val > val){  
    result = searchBST(root.left,val);  
}  
if (root.val < val){  
    result = searchBST(root.right,val);  
}  
return result;

很多录友写递归函数的时候习惯直接写 searchBST(root.left,val)，却忘了递归函数还有返回值。

递归函数的返回值是什么? 是左子树如果搜索到了val，要将该节点返回。如果不用一个变量将其接住，那么返回值不就没了。

所以要 result = searchBST(root.right,val); 。

整体代码如下：

代码实现

public TreeNode searchBST(TreeNode root, int val) {  
    if (root == null || root.val == val)  return root;  
    TreeNode result = null;  
    if (root.val > val){  
        result = searchBST(root.left,val);  
    }  
    if (root.val < val){  
        result = searchBST(root.right,val);  
    }  
    return result;  
}

解法二: {{迭代法}}

解题思路

迭代法

一提到二叉树遍历的迭代法，可能立刻想起使用栈来模拟深度遍历，使用队列来模拟广度遍历。

对于二叉搜索树可就不一样了，因为二叉搜索树的特殊性，也就是节点的有序性，可以不使用辅助栈或者队列就可以写出迭代法。

对于一般二叉树，递归过程中还有回溯的过程，例如走一个左方向的分支走到头了，那么要调头，在走右分支。

而对于二叉搜索树，不需要回溯的过程，因为节点的有序性就帮我们确定了搜索的方向。

例如要搜索元素为3的节点，我们不需要搜索其他节点，也不需要做回溯，查找的路径已经规划好了。

中间节点如果大于3就向左走，如果小于3就向右走，如图：

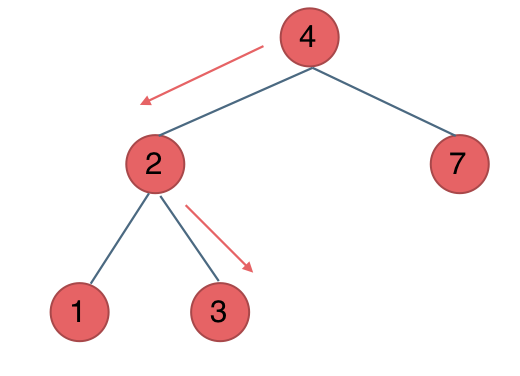
二叉搜索树

所以迭代法代码如下：

代码实现

// 迭代，利用二叉搜索树特点，优化，可以不需要栈  
public TreeNode searchBST(TreeNode root, int val) {  
    while (root != null)  
        if (val < root.val) root = root.left;  
        else if (val > root.val) root = root.right;  
        else return root;  
    return null;}

题目信息 98. 验证二叉搜索树

题目链接: https://leetcode.cn/problems/validate-binary-search-tree/
题目描述:
给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左

子树

只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

要知道中序遍历下，输出的二叉搜索树节点的数值是有序序列。

有了这个特性，验证二叉搜索树，就相当于变成了判断一个序列是不是递增的了。

解法一: {{递归}}

解题思路

递归三部曲：

确定递归函数，返回值以及参数

注意递归函数要有bool类型的返回值，我们在二叉树：递归函数究竟什么时候需要返回值，什么时候不要返回值？ (opens new window)中讲了，只有寻找某一条边（或者一个节点）的时候，递归函数会有bool类型的返回值。

其实本题是同样的道理，我们在寻找一个不符合条件的节点，如果没有找到这个节点就遍历了整个树，如果找到不符合的节点了，立刻返回。

代码如下：

TreeNode max;  
public boolean isValidBST(TreeNode root)

确定终止条件

如果是空节点是不是二叉搜索树呢？

是的，二叉搜索树也可以为空！

代码如下：

if (root == null) return true;

确定单层递归的逻辑

中序遍历，一直更新maxVal，一旦发现maxVal >= root->val，就返回false，注意元素相同时候也要返回false。

代码实现

TreeNode max;  
public boolean isValidBST(TreeNode root) {  
    if (root == null) return true;  
    //左  
    boolean left = isValidBST(root.left);  
    if (!left) return false;  
  
    //中  
    if (max != null && root.val <= max.val)  return false;  
    max = root;  
  
    //右  
    boolean right = isValidBST(root.right);  
    return right;  
}

//错误代码：过早返回True  在发现一个节点值大于 max 时就返回 true，这导致了对右子树的完全忽视  
TreeNode max;  
public boolean isValidBST(TreeNode root) {  
    if (root == null) return true;  
    //左  
    boolean left = isValidBST(root.left);  
    if (!left) return false;  
  
    //中  
    if (max != null && root.val > max.val)  return true;  
    max = root;  
  
    //右  
    boolean right = isValidBST(root.right);  
    return right;  
}

解法二: {{ 迭代法}}

代码实现

// 迭代  
public boolean isValidBST(TreeNode root) {  
    if (root == null) {  
        return true;  
    }  
    Stack<TreeNode> stack = new Stack<>();  
    TreeNode pre = null;  
    while (root != null || !stack.isEmpty()) {  
        while (root != null) {  
            stack.push(root);  
            root = root.left;// 左  
        }  
        // 中，处理  
        TreeNode pop = stack.pop();  
        if (pre != null && pop.val <= pre.val) {  
            return false;  
        }  
        pre = pop;  
  
        root = pop.right;// 右  
    }  
    return true;  
}