【机器学习】（基础篇五） —

【机器学习】（基础篇五） —— 逻辑回归

news2024/9/22 19:09:08

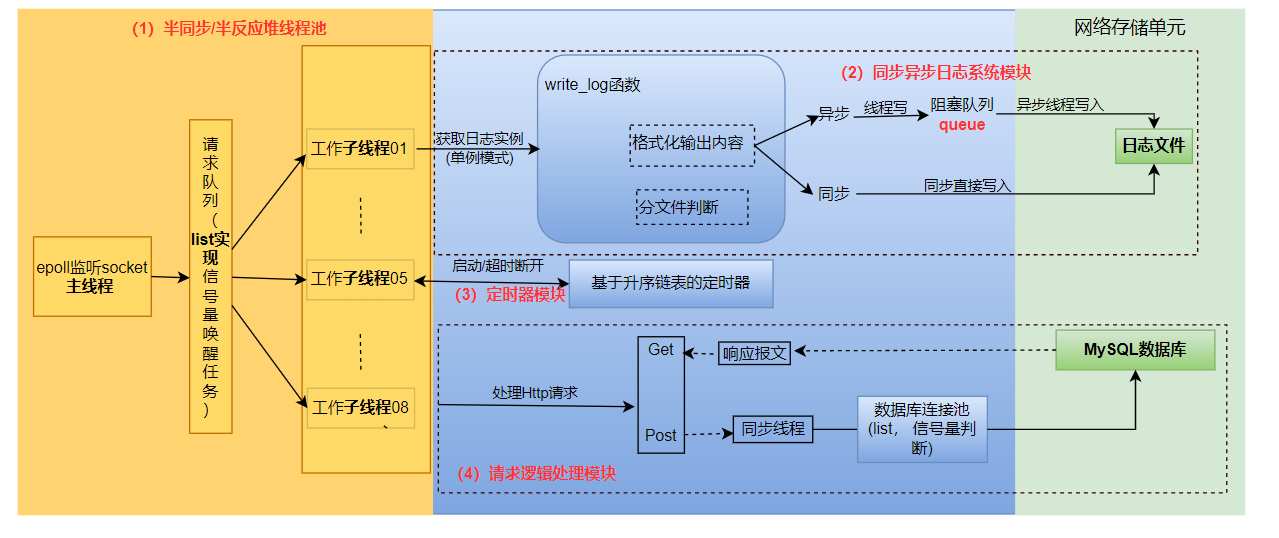
逻辑回归

逻辑回归（Logistic Regression）是一种广义线性模型，主要用于处理因变量为二分类或多分类（通过独热编码或多输出逻辑回归）的问题。尽管名字中带有“回归”二字，但实际上逻辑回归是一种分类算法，特别适用于估计某种事件发生的概率。实际上，“分类”是应用逻辑回归的目的和结果，但中间过程依旧是“回归”。

因为通过逻辑回归模型，我们得到的计算结果是0-1之间的连续数字，可以把它称为“可能性”（概率）。然后，给这个可能性加一个阈值，就成了分类。例如，利用逻辑回归估算出贷款违约的可能性>0.5，将借款人预判为坏客户。

逻辑回归和线性回归

在二分类问题中，只取0、1两个值。假设我们有这样一组数据：给不同的用户投放不同金额的广告，记录他们购买广告商品的行为，1代表购买，0代表未购买。

在这里插入图片描述假如此时依旧考虑线性回归模型，得到如下拟合曲线：

在这里插入图片描述

线性回归拟合的曲线，看起来和散点毫无关系，似乎没有意义。可以看出线性回归并不能很好的完成这个任务。

但我们可以在计算出预测值的结果后，加一个限制，即预测值＞0.5，就认为其属于1这一类，购买了商品，否则认为其不会购买，即：

$\left.\hat{y}=\left\{\begin{array}{c}1,f(x)>0.5\\0,f(x)<0.5\end{array}\right.\right.$

由于拟合方程为

$\hat{y}=0.34*x$

那么上面的限制就等价于：

$\left.\hat{y}=\left\{\begin{array}{c}1,x>1.47\\0,x\leq1.47\end{array}\right.\right.$

这样就相当于是当x大于1.47时，将y预估为1，即将其判断为会进行购买；而x小于1.47时，将y预估为0，即将其判断为不会进行购买

这种形式，非常像阶跃函数：

在这里插入图片描述

把阶跃函数向右平移一下，就可以比较好地拟合上面的散点图。但是阶跃函数有个问题，它不是连续函数。我们希望可以用一个单调可导的函数来代替阶跃函数。

sigmoid函数

因为阶跃函数不好进行数学上的计算，不连续，也不可导，所以使用sigmoid函数对其进行代替逻辑回归算法的拟合函数，相当于优化后的阶跃函数：

$f(x)=\frac1{1+e^{-z}}$

其函数图像如下：

在这里插入图片描述

sigmoid函数是一个s形曲线，就像是阶跃函数的温和版，阶跃函数在0和1之间是突然的起跳，而sigmoid有个平滑的过渡。

从图形上看，sigmoid曲线就像是被掰弯捋平后的线性回归直线，将取值范围(−∞,+∞)映射到(0,1) 之间，更适宜表示预测的概率，即事件发生的“可能性” 。还是用上面广告的例子，如果使用sigmoid函数进行表示，然后有一个点的x为1.5，其在sigmoid函数中对应的y的预估值为0.7，则表示又70%的会进行购买。

此处的sigmoid函数的z可以看作是嵌套函数，z是一个线性组合 $z=w_1x_1+w_2x_2+...+w_nx_n+b$

结合起来就是 $P(y=1|x;w,b)=\frac{1}{1+e^{-(b+w_1x_1+w_2x_2+\cdots+w_px_p)}}$

逻辑函数的构造算是完成了。找到了合适的函数，下面就是求函数中的未知参数向量 $w$ 了。

因为sigmoid函数最终给出的是一个概率，所以我们需要的损失函数就是用来计算模型预测的概率与实际观察到的类别的差异，对数损失函数可以实现这个要求，它会对错误的预测进行惩罚。

单个样本的对数损失函数的表达式为：

$L(p,y)=-y\log(p)-(1-y)\log(1-p)$

这里，当 y=1（正例）时，损失函数简化为 −log⁡§，这意味着如果模型预测的概率 p 接近1，则损失较小；反之，如果 p 接近0，则损失很大。同理，当 y=0（反例）时，损失函数简化为 −log⁡(1−p)，意味着如果模型预测的概率 p接近0，则损失较小；反之，如果 p 接近1，则损失很大。让损失函数最小，最中就能得到和真实情况最接近的预测情况所需要的参数w和b

为了优化参数 w 和 b，我们需要最小化所有样本的损失函数的平均值，也就是交叉熵损失（Cross-Entropy Loss），其数学表达式为：

$J(w,b)=-\frac1m\sum_{i=1}^m[y^{(i)}\log(p^{(i)})+(1-y^{(i)})\log(1-p^{(i)})]$

其中，mm 是样本数量，p(i)是第 i 个样本的预测概率。

使用梯度下降法求出其中的参数

【示例】sklearn中有一个乳腺癌数据集用于二分类，刚好可以使用逻辑回归对其分类

from sklearn.datasets import load_breast_cancer 
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report
 
# 导入数据集
cancer = load_breast_cancer()
#print(cancer)
# 提取中数据集中的数据
data=cancer["data"]
# 提取数据集中的特征名称
col = cancer['feature_names']
# 将特征名字和数据组合，并转换为DataFrame类型
x = pd.DataFrame(data,columns=col)
# 目标值的提取同理
target = cancer.target.astype(int)
y = pd.DataFrame(target,columns=['target'])
# 划分训练集和测试集
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3,random_state=1)
model = LogisticRegression()
model.fit(x_train, y_train)
y_pred = model.predict(x_test)
# 输出模型报告
print(classification_report(y_test, y_pred))