
一、说明
K-means 的目标是将一组观测值划分为 k 个聚类,每个观测值分配给均值(聚类中心或质心)最接近的聚类,从而充当该聚类的代表。
在本文中,我们将全面介绍 k 均值聚类(最常用的聚类方法之一)及其组成部分的所有内容。我们将了解聚类,为什么它很重要,以及它的应用。
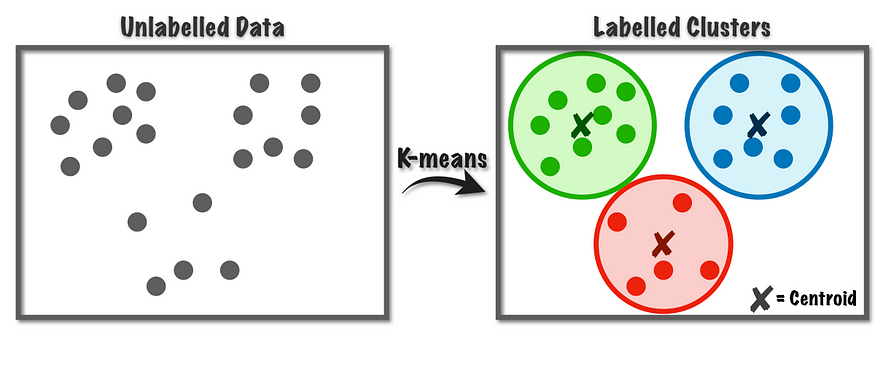
二、什么是 K-means 聚类?
K-Means 聚类是一种流行的无监督机器学习算法,用于将数据集划分为一组不同的、不重叠的组或聚类。目标是以这样一种方式对数据点进行分组,即同一聚类中的点彼此之间比与其他聚类中的点更相似。该技术广泛应用于数据挖掘、市场细分、图像压缩以及其他需要模式识别的领域。
2.1 K-means 中使用的数学概念
在我们开始计算 k 均值之前,我们将讨论 K 均值中使用的数学概念。
- 质心:这些是聚类的中心点,在每次迭代中都会重新计算,以作为分配给聚类的点的平均值。
- 欧几里得距离:这是 K-Means 中最常用的距离度量。它计算欧几里得空间中两点之间的直线距离。
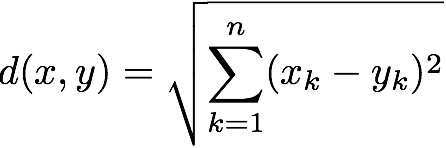
对于 n 维的 X(x1,x2,...,xn) 和 Y(y1,y2,...,yn) 2 个点,使用此公式测量欧几里得距离。
- 惯性:它衡量集群的分布程度。它是每个数据点与其分配的质心之间的平方距离之和。目标是将惯性降至最低。
WCSS = d1² + d2²+ d3² + ...........+ dn²
2.2 K-means是如何工作的?
# Generating Data
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
# Parameters
n_samples = 300
n_features = 2
centers = 4
# Generate data
X, y = make_blobs(n_samples=n_samples, n_features=n_features, centers=centers, cluster_std=3, random_state=42)
# Visualize the data
plt.scatter(X[:, 0], X[:, 1], s=50, cmap='viridis')
plt.title("Initial Data")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()
from sklearn.cluster import KMeans
kmeans = KMeans(n_init = 10, n_clusters = 4, verbose=100)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)
plt.scatter(X[y_kmeans == 0, 0], X[y_kmeans == 0, 1], s = 60, c = 'red', label = 'Cluster1')
plt.scatter(X[y_kmeans == 1, 0], X[y_kmeans == 1, 1], s = 60, c = 'blue', label = 'Cluster2')
plt.scatter(X[y_kmeans == 2, 0], X[y_kmeans == 2, 1], s = 60, c = 'green', label = 'Cluster3')
plt.scatter(X[y_kmeans == 3, 0], X[y_kmeans == 3, 1], s = 60, c = 'yellow', label = 'Cluster4')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s = 100, c = 'black', label = 'Centroids')
plt.legend()
plt.show()
- 初始化:
- 选择簇数 K。
- 随机初始化 K 个质心,它们是数据集中表示每个聚类中心的点。
2. 分配步骤:
- 根据欧几里得距离将每个数据点分配给最近的质心。这将创建 K 个聚类。
我们计算一个点到每个质心的欧几里得距离,并将其放入距离最小的聚类中。
3. 更新步骤:
- 通过取分配给每个聚类的所有数据点的平均值来计算新的质心。
我们计算聚类中所有点的平均值,以获得新的质心。

4.重复:
- 使用新的质心重复分配和更新步骤,直到质心不再更改或更改低于预定义的阈值。

生成上述图像的代码在此处。
三、如何确定质心的数量?
3.1 弯头法
肘部方法是一种用于确定 K-Means 聚类中最佳聚类数的技术。这个想法是对 K 的值范围运行 K-Means,并计算从每个点到其分配的质心的距离平方和(称为惯性或簇内平方和)。随着 K 的增加,惯性减小,因为点更接近它们的质心。
目标是找到“肘点”,其中下降速度急剧减慢,表明随着 K 的增加,回报递减,即在肘点之后增加 K 的值没有多大好处。
WCSS = d1² + d2² + d3² + ...........+ dn²
我们通常计算前 10 个聚类的惯性。对于 K = 数据点数,惯性将为零。
from sklearn.cluster import KMeans
wcss = []
for i in range(1, 11):
kmeans = KMeans(n_init = 10, n_clusters = i)
kmeans.fit(X)
wcss.append(kmeans.inertia_)
plt.title("Elbow Method")
plt.xlabel("Number of Clusters(k)")
plt.ylabel("WCSS")
plt.plot(range(1,11),wcss)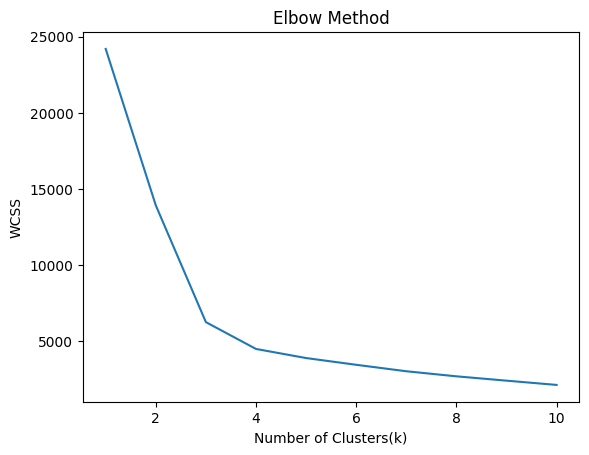
因此,集群的数量可以是 3 个或 4 个。
肘部方法有一些限制,例如:
- 肘点的选择是主观的。
- 它不适用于所有数据集,例如当聚类具有不规则形状或大量特征时。
3.2 剪影分数
Silhouette 分数是一个指标,用于量化集群的质量。它适用于任何聚类算法。
剪影分数的值从 -1 到 +1 不等。
- +1 : 良好(集群分离良好)
- 0 : 集群彼此靠近
- -1 : 错误(错误的聚类)
内聚力: 同一聚类中元素彼此接近的程度。(它衡量集群的紧凑性。
分离: 它指的是不同的集群彼此之间有多么不同或分辨得多么好。
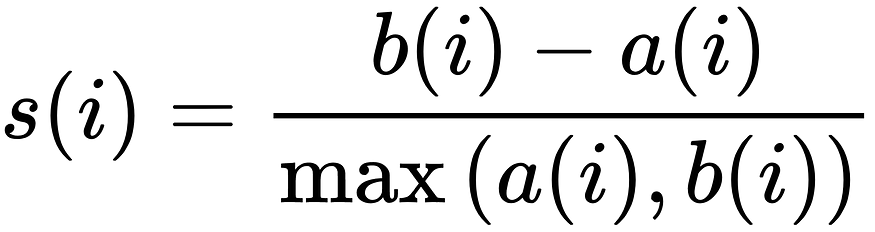
S(i) 是剪影分数。
a(i) 是所取点与其自身聚类中所有点的平均距离。它代表着凝聚力。
b(i) 是所取点与剩余最近聚类的所有点之间的平均聚类距离。它代表分离。

from sklearn.metrics import silhouette_score
sil = []
for i in range(2, 11):
kmeans = KMeans(n_clusters=i)
cluster_labels = kmeans.fit_predict(X)
silhouette_avg = silhouette_score(X, cluster_labels)
sil.append(silhouette_avg)
plt.xlabel("Number of Clusters(k)")
plt.ylabel("Silhouette Score")
plt.plot(range(2,11),sil)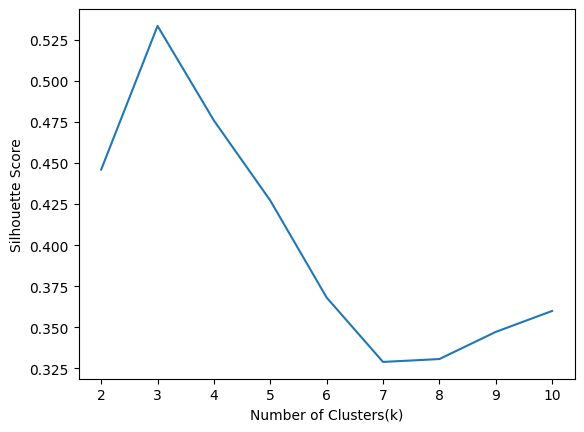
根据轮廓分数,我们应该假设 k=3,因为对于 3 个聚类,分数是最大的。
四、如何初始化质心?
4.1 K-均值++
K-Means++ 是 K-Means 聚类算法的高级版本,它改进了质心的初始选择,旨在提高聚类结果和收敛速度。标准的 K-Means 算法对质心的初始放置很敏感,初始化不良会导致聚类次优和收敛速度变慢。K-Means++ 通过使用更智能的初始化策略来解决这个问题。
4.2 K-Means++ 初始化的步骤
1. 选择第一个质心:
• 从数据集中随机选择第一个质心。
2. 选择后续质心:
• 对于每个后续质心,计算从每个
数据点 x 到最近的已选质心的距离 D(x)。
• 从数据点中选择下一个质心,其概率与 D(x)² 成正比。概率最大的点作为质心。(我们采用概率而不是距离本身来减少异常值的影响。
3. 重复:
• 重复该过程,直到选择 K 个质心。
4. 继续使用标准 K-Means:
• 使用这些 K 质心作为初始起点,并运行标准 K-Means 算法


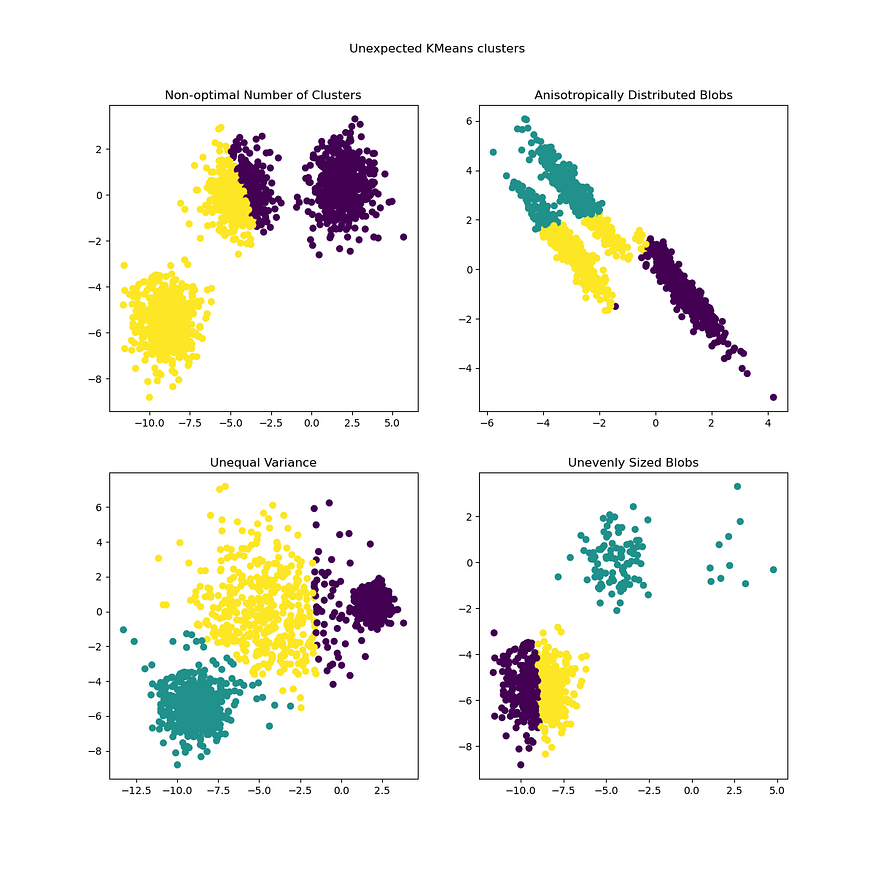
五、K-means的假设和局限性
- 假设簇是球形和各向同性(不是不规则形状)。
- 假定聚类具有相似的大小。
- 假设所有聚类都具有相似的方差。
- 集群的数量是预定义的。
- 当聚类分离良好时,此算法效果最佳。
- K 均值不能在存在异常值的情况下应用(因为质心会移动太多并且无法正确分配)
六、结论
K-Means 简单性和效率使其成为各种应用的热门选择,包括图像分割、市场分割和模式识别。尽管它很简单,但它为各个领域的许多应用程序提供了坚实的基础。但是,它对质心的初始放置很敏感,这可能导致次优聚类。尽管存在一些局限性,例如对 K 选择的敏感性以及卡在局部最小值中的可能性,但 K-Means 仍然是数据分析和机器学习中一种基本且高效的聚类技术。
K-Means 有其局限性,其他聚类算法(如 DBSCAN 和 GMM)可以克服这些局限性。



















