插入的节点的颜色都是红色的，因为插入红色对树的影响较小，如果插入的是黑色节点，那么必须要左复杂的平衡操作。

红黑树插入节点情景分析

情景1：红黑树为空树

那么直接让插入节点x 作为根节点，并且设置成黑色。

情景2：插入节点的Key已存在

直接更新节点为插入结点的值。

情景3：插入节点的父节点为黑色节点

由于插入的节点是红色的，当插入节点的父节点是黑色的时候，并不会影响红黑树的平衡，直接插入即可，无需做自平衡。

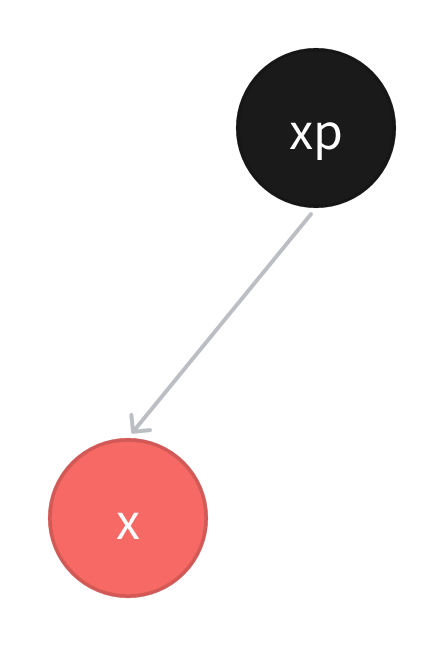
情景4：插入节点的父节点为红色

情景4.1 叔叔节点存在并且为红色节点

根据红黑树性质可知，红色节点不能相连，那么爷爷节点肯定为黑色节点。
那么解决方案就是：将父亲节点和叔叔节点改为黑色，爷爷节点改为红色，但爷爷节点可能是根节点，也可能爷爷的父亲也是红色节点，所以还需要对爷爷节点进行处理，直到平衡为止。

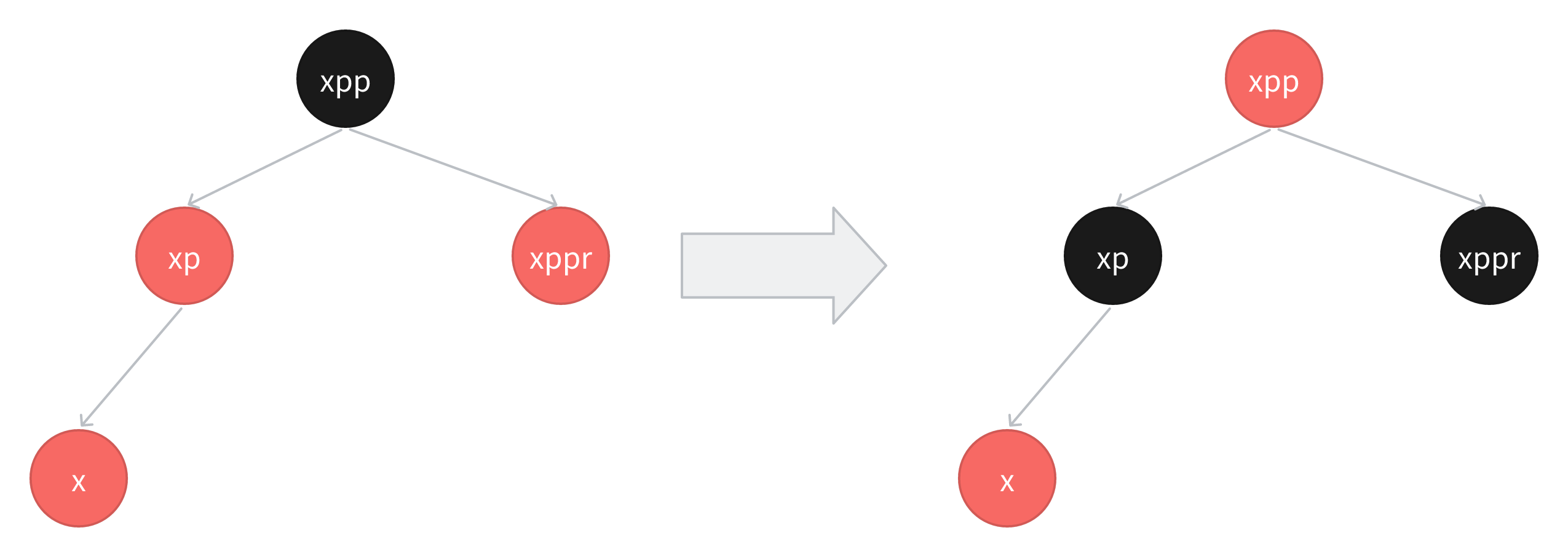
情景4.2 叔叔节点存在而且是黑色节点

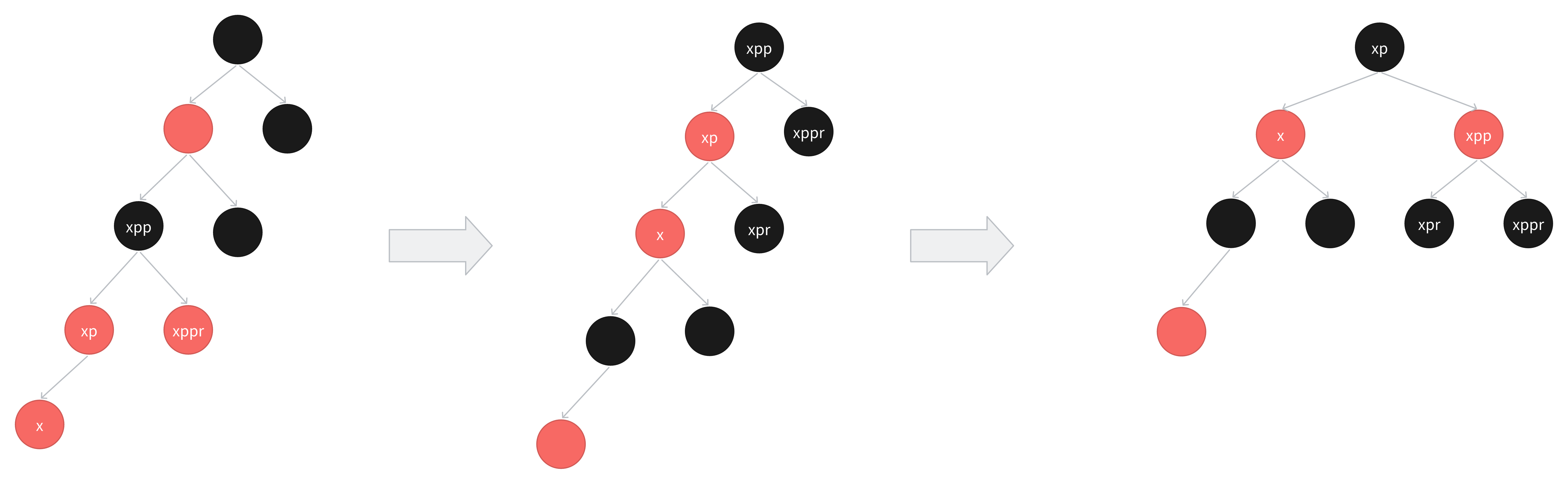
为什么叔叔节点会是黑色节点呢，一开始我也想了很久。后来找到了下面这个样例，才觉得是可能的。
首先看下图左边的红黑树，此时插入了一个新节点x，经过第一轮变换后，到了中间的红黑树，此时x节点变成了之前的爷爷节点，现在应该对新的x节点进行转换，它发现它的叔叔是黑色节点，那么首先将爷爷节点进行右旋，xp 成为了新的根节点，再将xp改为黑色节点，xpp改为红色节点，就完成了第二次转换，如下图右边的红黑树。

情景4.3 叔叔节点不存在

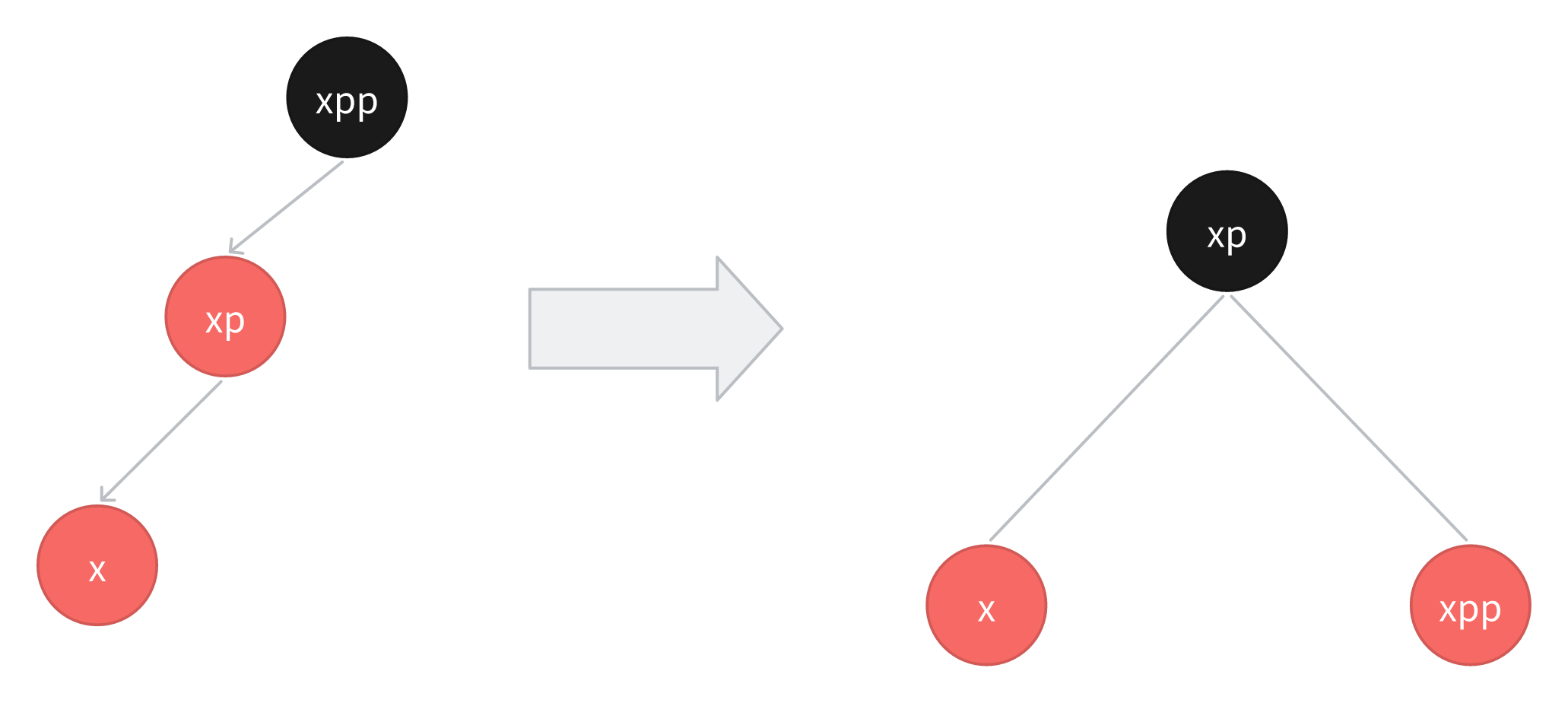
4.3.1 插入节点是父亲节点的左孩子

直接将xpp进行右旋，并且将xp改为黑色，xpp改为红色。

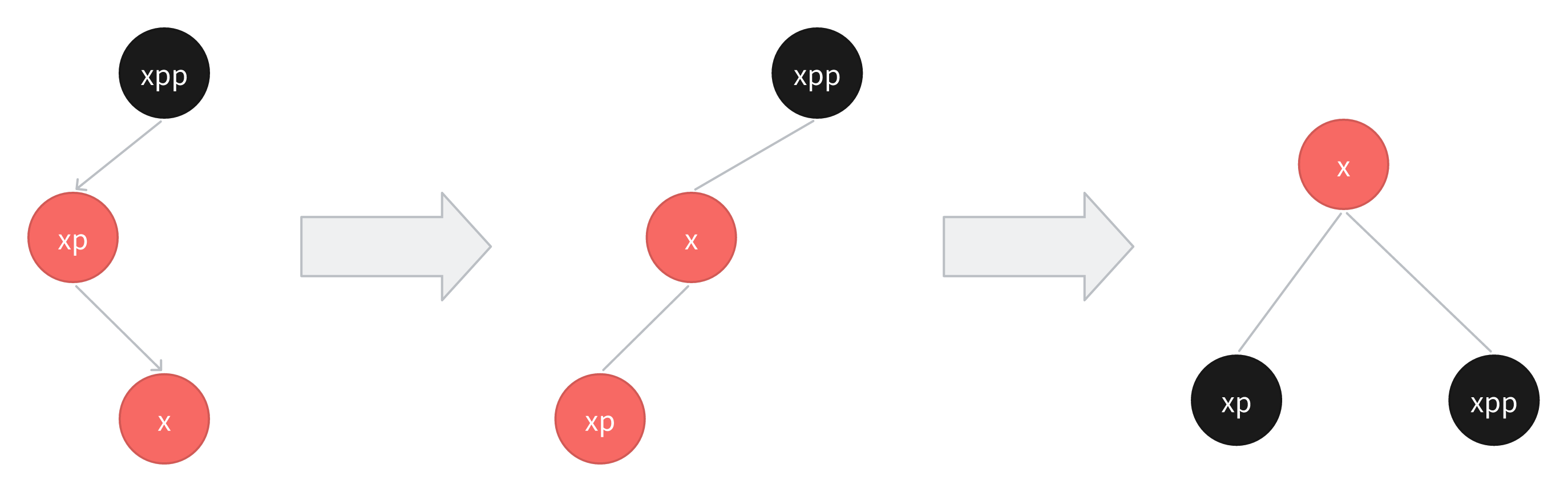
4.3.2 插入节点是父亲节点的右孩子

如果插入节点是父亲节点的右孩子，那么首先需要将xp左旋，然后就跟4.3.1案例一样了，然后直接将xpp右旋。

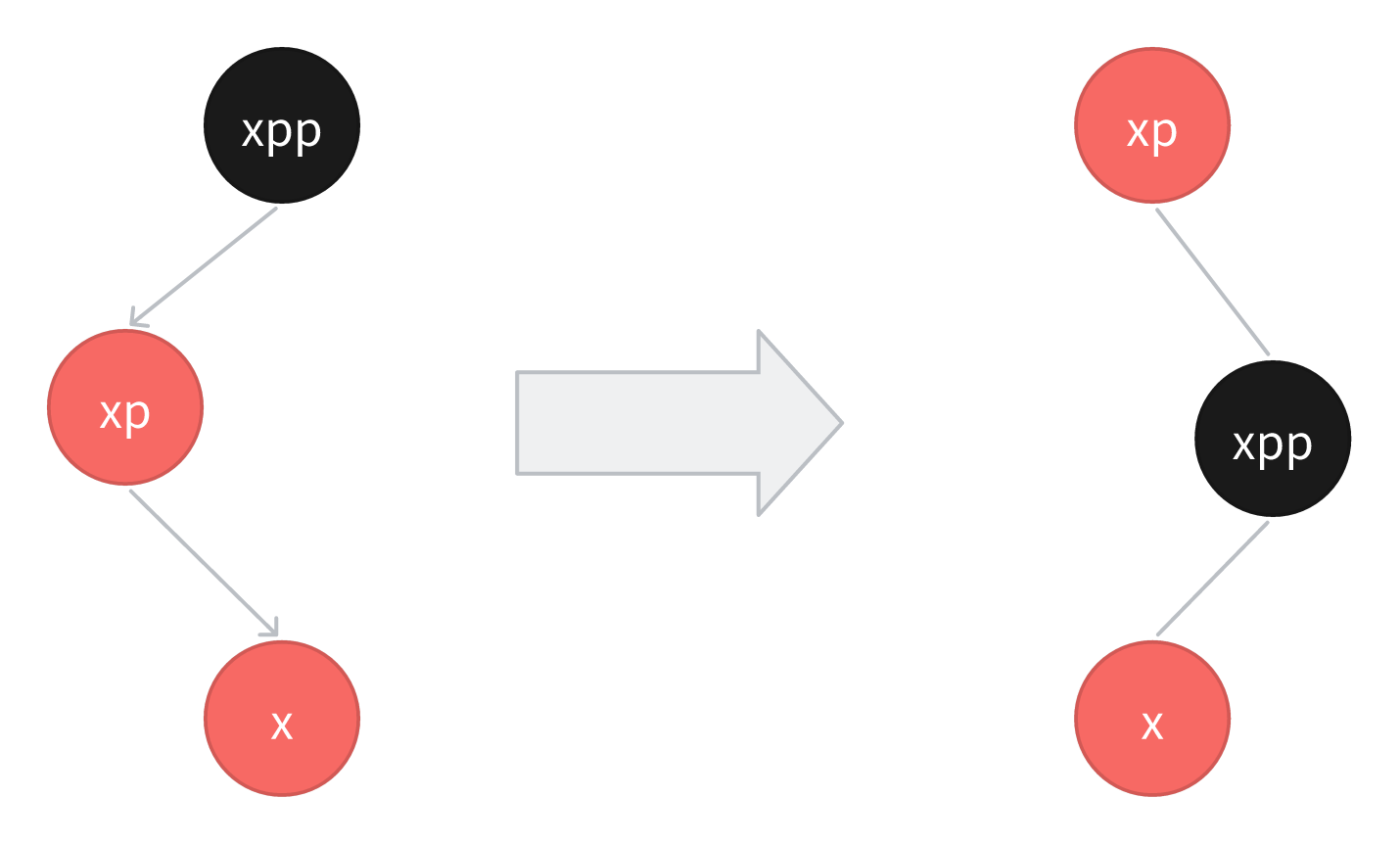
我之前有个疑问，为啥不可以直接将xpp右旋呢，比如下面，但这样是不对的，因为这样违反了规则5：从任一结点到其每个叶子的所有路径都包含相同数目的黑色节点。所以需要先将xp左旋，然后在将xpp右旋，这样就满足了规则5。

以上展示的是父节点是爷爷的左孩子，关于父节点是爷爷的右孩子同理，就不在赘述了。

插入源代码

static <K, V> TreeNode<K, V> balanceInsertion(TreeNode<K, V> root,
                                              TreeNode<K, V> x) {
    // x 为插入节点，将其颜色设置为null
    x.red = true;
    TreeNode<K, V> xp, xpp, xppl, xppr;
    while (true) {
        xp = x.parent;
        // 1.如果插入节点的父亲为null，则它是根节点
        // 并将其设置成黑色
        if (xp == null) {
            x.red = false;
            return x;
            // 如果父亲节点为黑色，那么插入一个红色节点不会影响平衡，直接返回
        } else if (!xp.red) {
            return root;
        } else {
            // TODO: 如果父亲节点是根节点的话，那不应该是黑色嘛
            xpp = xp.parent;
            if (xpp == null) {
                return root;
            }
        }
        // 此时父亲肯定是红色
        xppl = xpp.left;
        xppr = xpp.right;
        if (xp == xppl) {
            if (xppr != null && xppr.red) {
                xppr.red = false;
                xp.red = false;
                xpp.red = true;
                // 将爷爷节点设置为插入节点，因为爷爷节点变成了红色，
                // 可能会破坏平衡，所以需要重新走一遍平衡
                x = xpp;
            } else {
                // 到这里，证明它的叔叔节点为空或者为黑色

                // 如果插入节点是父亲节点的右孩子
                if (x == xp.right) {
                    // 先将父节点左旋
                    x = xp;
                    root = rotateLeft(root, x);
                    xp = x.parent;
                    xpp = xp == null ? null : xp.parent;
                }
                // 如果有父节点
                if (xp != null) {
                    // 父节点设置成黑色
                    xp.red = false;
                    if (xpp != null) {
                        // 爷爷节点设置成红色
                        xpp.red = true;
                        // 将爷爷节点右旋
                        root = rotateRight(root, xpp);
                    }
                }
            }
        } else {
            if (xppl != null && xppl.red) {
                xppl.red = false;
                xp.red = false;
                xpp.red = true;
                x = xpp;
            } else {
                if (x == xp.left) {
                    x = xp;
                    root = rotateRight(root, x);
                    xp = x.parent;
                    xpp = xp == null ? null : xp.parent;
                }
                if (xp != null) {
                    xp.red = false;
                    if (xpp != null) {
                        xpp.red = true;
                        root = rotateLeft(root, xpp);
                    }
                }
            }
        }
    }
}

static <K, V> TreeNode<K, V> rotateLeft(TreeNode<K, V> root, TreeNode<K, V> p) {
    if (p == null || p.right == null)
        return root;
    TreeNode<K, V> pp = p.parent; // 父节点
    TreeNode<K, V> pr = p.right; // 右孩子
    TreeNode<K, V> prl = pr.left;// 右孩子的左孩子
    p.right = prl;
    if (prl != null) {
        prl.parent = p;
    }
    pr.parent = pp;
    if (pp == null) {
        root = pr;
        root.red = false;
    } else if (p == pp.left) {
        pp.left = pr;
    } else {
        pp.right = pr;
    }
    pr.left = p;
    p.parent = pr;
    return root;
}

static <K, V> TreeNode<K, V> rotateRight(TreeNode<K, V> root, TreeNode<K, V> p) {
    if (p == null || p.left == null)
        return root;

    TreeNode<K, V> pp = p.parent;
    TreeNode<K, V> pl = p.left;
    TreeNode<K, V> plr = pl.left;
    p.left = plr;
    if (plr != null) {
        plr.parent = p;
    }
    // 更新旋转节点的父节点
    pl.parent = pp;
    if (pp == null) {
        root = pl;
        root.red = false;
    } else if (p == pp.left) {
        pp.left = pl;
    } else {
        pp.right = pl;
    }
    pl.right = p;
    p.parent = pl;
    return root;
}