PDF文档公众号回复关键字:20240817

1 完善程序 (单选题 ,每小题3分,共30分)
最大公约数之和
对于一个 1到 n的排列 P(即 1 到 n 中每一个数在 P中出现了恰好一次),令 q[i] 为第 i个位置之后第一个比 P[i] 值更大的位置,如果不存在这样的位置,则 q[i] = n + 1。举例来说,如果 n = 5 且 P 为 1 5 4 2 3 ,则 q 为2 6 6 5 6。
下列程序读入了排列 P ,使用双向链表求解了答案。试补全程序
01 #include <iostream>
02 using namespace std;
03
04 const int N = 100010;
05 int n;
06 int L[N], R[N], a[N];
07
08 int main() {
09 cin >> n;
10 for (int i = 1; i <= n; ++i) {
11 int x;
12 cin >> x;
13 ① ;
14 }
15
16 for (int i = 1; i <= n; ++i) {
17 R[i] = ② ;
18 L[i] = i - 1;
19 }
20
21 for (int i = 1; i <= n; ++i) {
22 L[ ③ ] = L[a[i]];
23 R[L[a[i]]] = R[ ④ ];
24 }
25
26 for (int i = 1; i <= n; ++i) {
27 cout << ⑤ << " ";
28 }
29
30 cout << endl;
31 return 0;
32 }
1 ①处应填( )
2 ②处应填( )
3 ③处应填( )
4 ④处应填( )
5 ⑤处应填( )
2 相关知识点
1) 计数排序
计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用,具体思路为
统计相同元素出现次数
根据统计的结果将序列回收到原来的序列中
#include<bits/stdc++.h>
using namespace std;
int main(){
int a[10]={3,4,2,7,5,4,3,3,3,5};
int cnt[7]={0};//cnt数组记录对应下标出现次数
for(int i=0;i<10;i++){
cnt[a[i]]++;
}
for(int i=0;i<=7;i++){//枚举对应范围的数 从最小到最大,本示例从0~7即可
while(cnt[i]>0){//一个数字出现多次时,cnt[i]为对应的数为出现几次
cout<<i<<" ";
cnt[i]--;
}
}
return 0;
}
/*
输出
2 3 3 3 3 4 4 5 5 7
*/
排列应用
对于一个 1到 n的排列 P(即 1 到 n 中每一个数在 P中出现了恰好一次),由于1~n中的每个数只出现1次,所以对排列中的数进行排序,同时记录其在原数组的下标位置
#include<bits/stdc++.h>
using namespace std;
int main(){
int P[6]={0,1,5,4,2,3};
int a[6]={0};
/*
以P[i]为a下标,a的值记录P[i]中的下标
a的下标顺序对P中的数进行了排序
*/
for(int i=1;i<=5;i++){
a[P[i]]=i;
}
for(int i=1;i<=5;i++){//输出对P排序后在P中的下标
cout<<a[i]<<" ";
}
cout<<endl;
for(int i=1;i<=5;i++){//输出通过a数组对P排序后的值
cout<<P[a[i]]<<" ";
}
return 0;
}
/*
输出
1 4 5 3 2
1 2 3 4 5
*/
2 链表
链表是一种常见的数据结构,它是由一系列节点(Node)组成,每个节点包含两部分:数据域和指针域。数据域用于存储数据,指针域用于存储下一个节点的地址。链表的第一个节点称为头节点(Head),最后一个节点称为尾节点(Tail),尾节点的指针域指向空(NULL)
单向链表
一种最简单的结点结构如图所示,它是构成单链表的基本结点结构
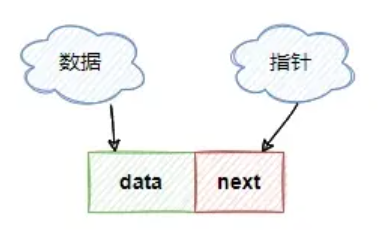
在结点中数据域用来存储数据元素,指针域用于指向下一个具有相同结构的结点。
因为只有一个指针结点,称为单链表
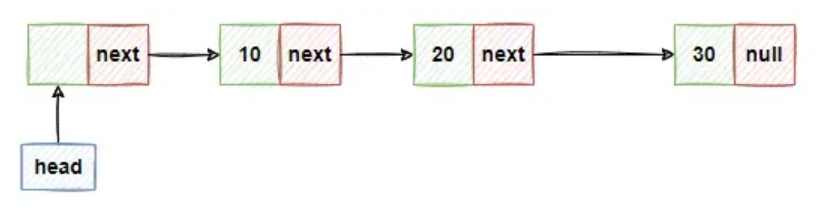
双向链表
单向链表只有一个方向,结点只有一个后继指针 next 指向后面的结点。
双向链表,顾名思义,它支持两个方向,每个结点不止有一个后继指针 next 指向后面的结点,还有一个前驱指针 prev 指向前面的结点
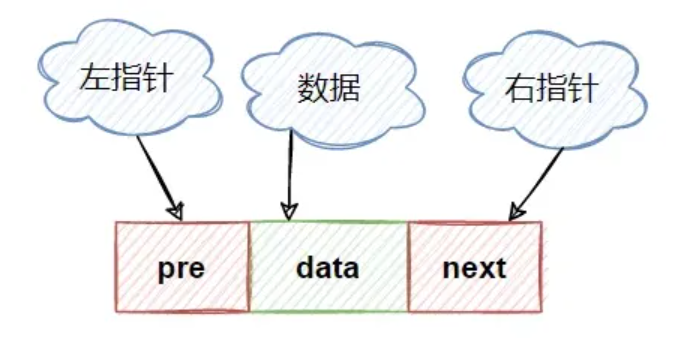
在结点中数据域用来存储数据元素,指针域用于指向下一个具有相同结构的结点。
因为有1左指针节点和1个右指针节点,同时指向2个方向的节点,因此称为双向链表

3 思路分析
1 ①处应填( a[x]=i )
分析
此处使用计数排序思想,通过a数组从小到大记录在排列P的位置
比如P 1 5 4 2 3
对应a 1 4 5 3 2
10 for (int i = 1; i <= n; ++i) {
11 int x;
12 cin >> x;
13 ① ;
14 }
2 ②处应填( i+1 )
分析
L数组代表P数组的左指针
L数组代表P数组的右指针
例如P 1 5 4 2 3 对应1 2 3 4 5下标
则
L 0 0 1 2 3
R 2 3 4 5 6
所以此处填i+1
16 for (int i = 1; i <= n; ++i) {
17 R[i] = ② ;
18 L[i] = i - 1;
19 }
3 ③处应填( R[a[i]] )
分析
从小到大去除当前数字,当前数字是数组中最小的数字
去除当前数字后,下一个带去除的,是数字中最小数字
此处通过双向链表去除当前数字
当前节点的后1个节点左指针指向当前节点前1个节点
当前节点的前1个节点右指针指向当前节点后1个节点
所以
22 L[ R[a[i]] ] = L[a[i]];
23 R[L[a[i]]] = R[a[i]];
21 for (int i = 1; i <= n; ++i) {
22 L[ ③ ] = L[a[i]];
23 R[L[a[i]]] = R[ ④ ];
24 }
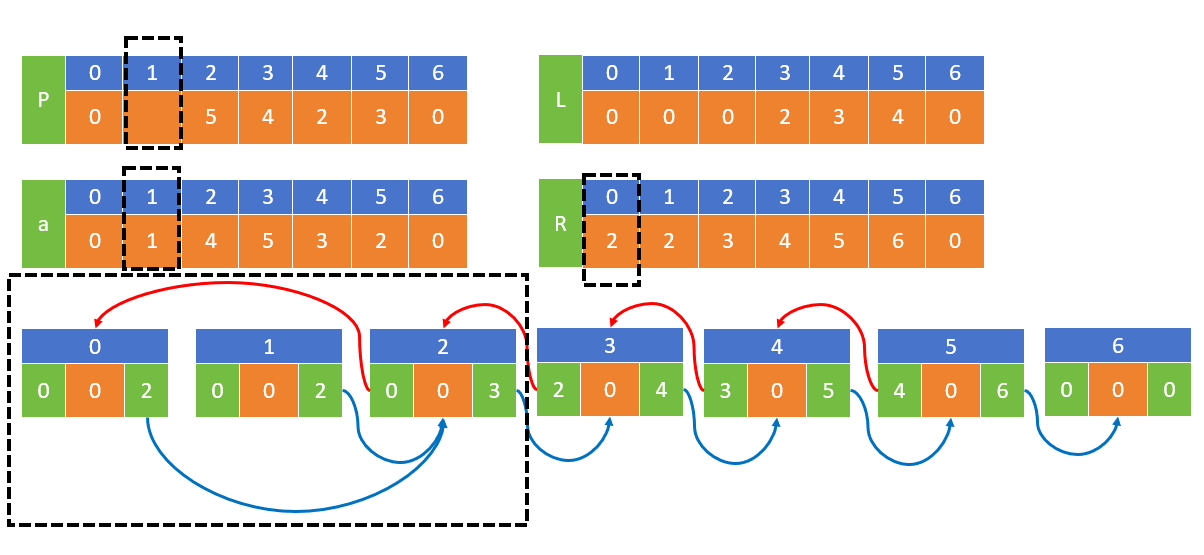
以 1 5 4 2 3为例,第1个删除1
删除1前
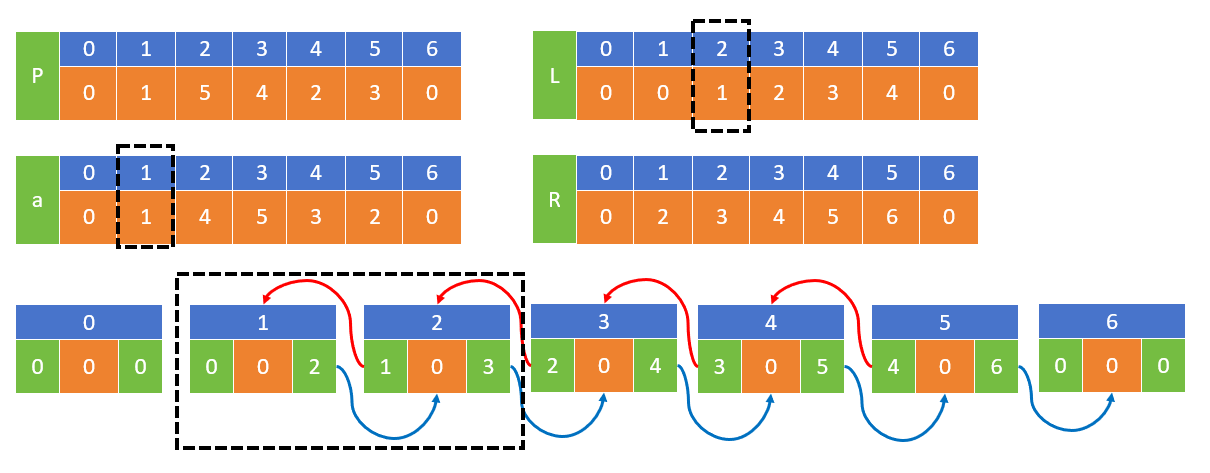
删除1后,2节点左指针指向0节点,0节点右节点指向2节点,1就从链表中被删除了
1节点右指针指向2节点,没有改变,1后面比1大的第1个节点为2节点
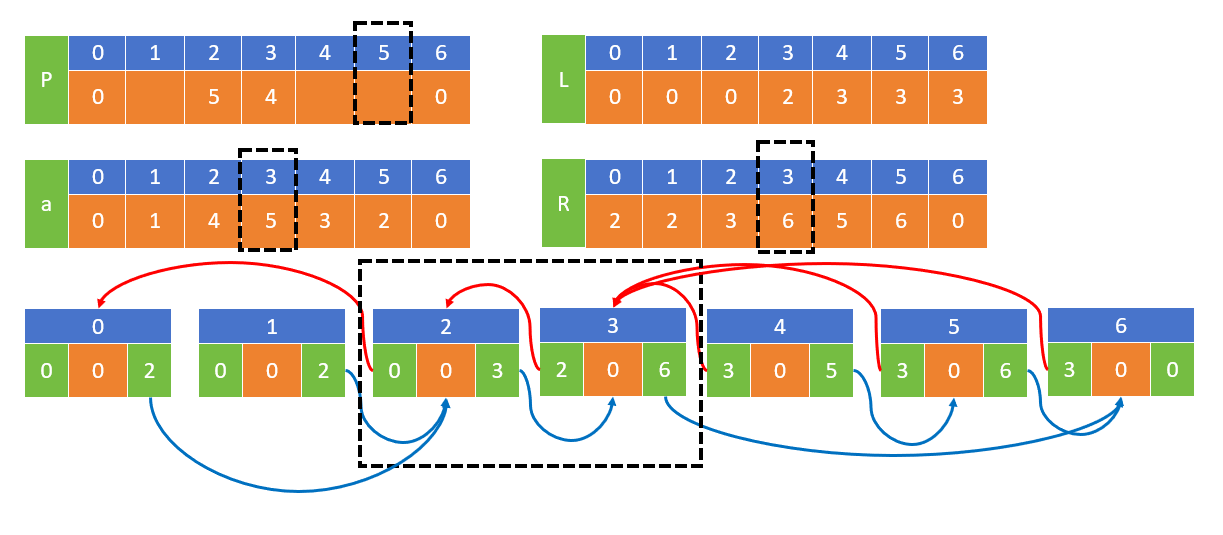
例如 1 5 4 2 3 中的5,后面4 2 3 都比5小,因此应该是n+1=5+1=6
按照数字从小到大对链表进行删除,5为最后1个被删除的
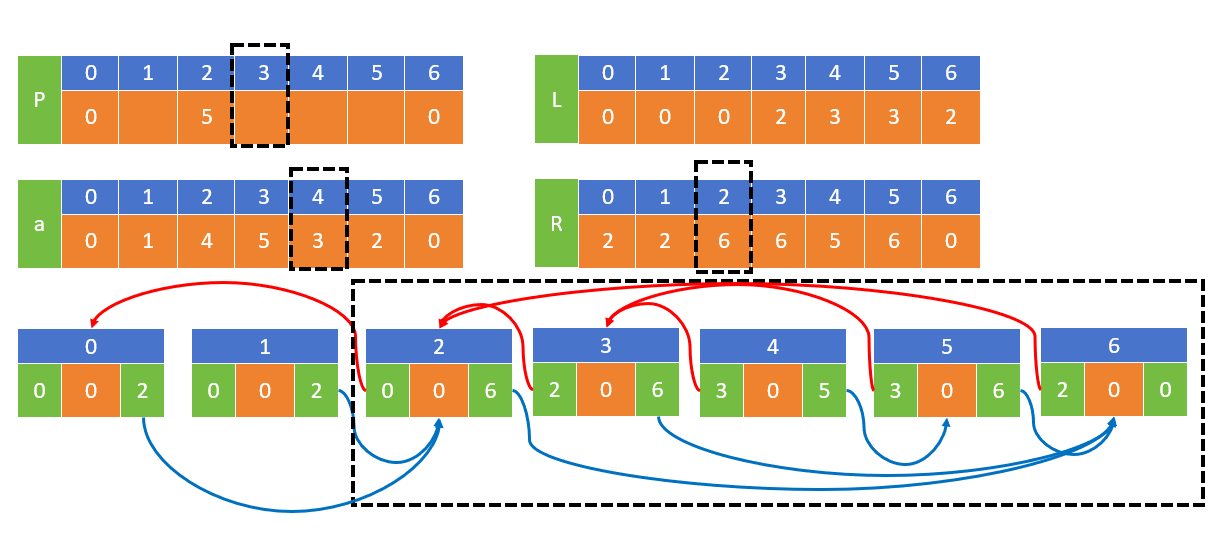
删除4前,5对应节点为2,右指针指向3节点(数字4)
删除4后,右指针指向6节点
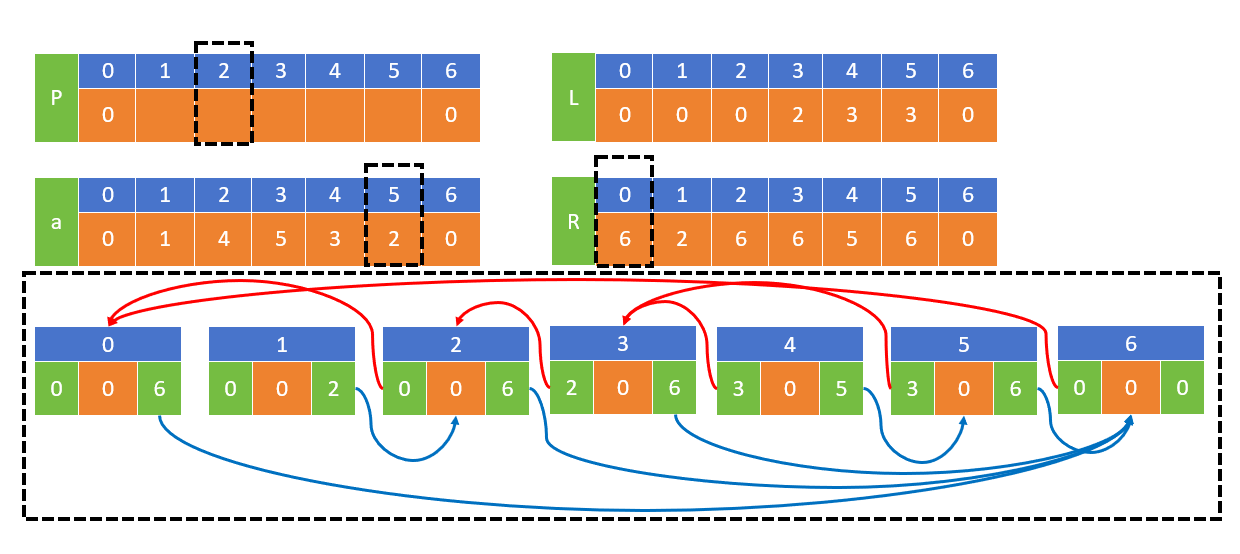
删除5后,对应R数组的值,以及左右指针如下
4 ④处应填( a[i] )
分析
同3
5 ⑤处应填( R[i] )
分析
一开始R数组是当前数字的右边节点
从小到大逐一删除,如果右边比当前大,当前的右指针不会被删除
如果右边比自己小会先删除右边,删除右边时,会把当前的右指针指向更大的
这种删除方法可以保证R[i]是右边第1个比R[i]大的数
所以此处填R[i]
26 for (int i = 1; i <= n; ++i) {
27 cout << ⑤ << " ";
28 }



















