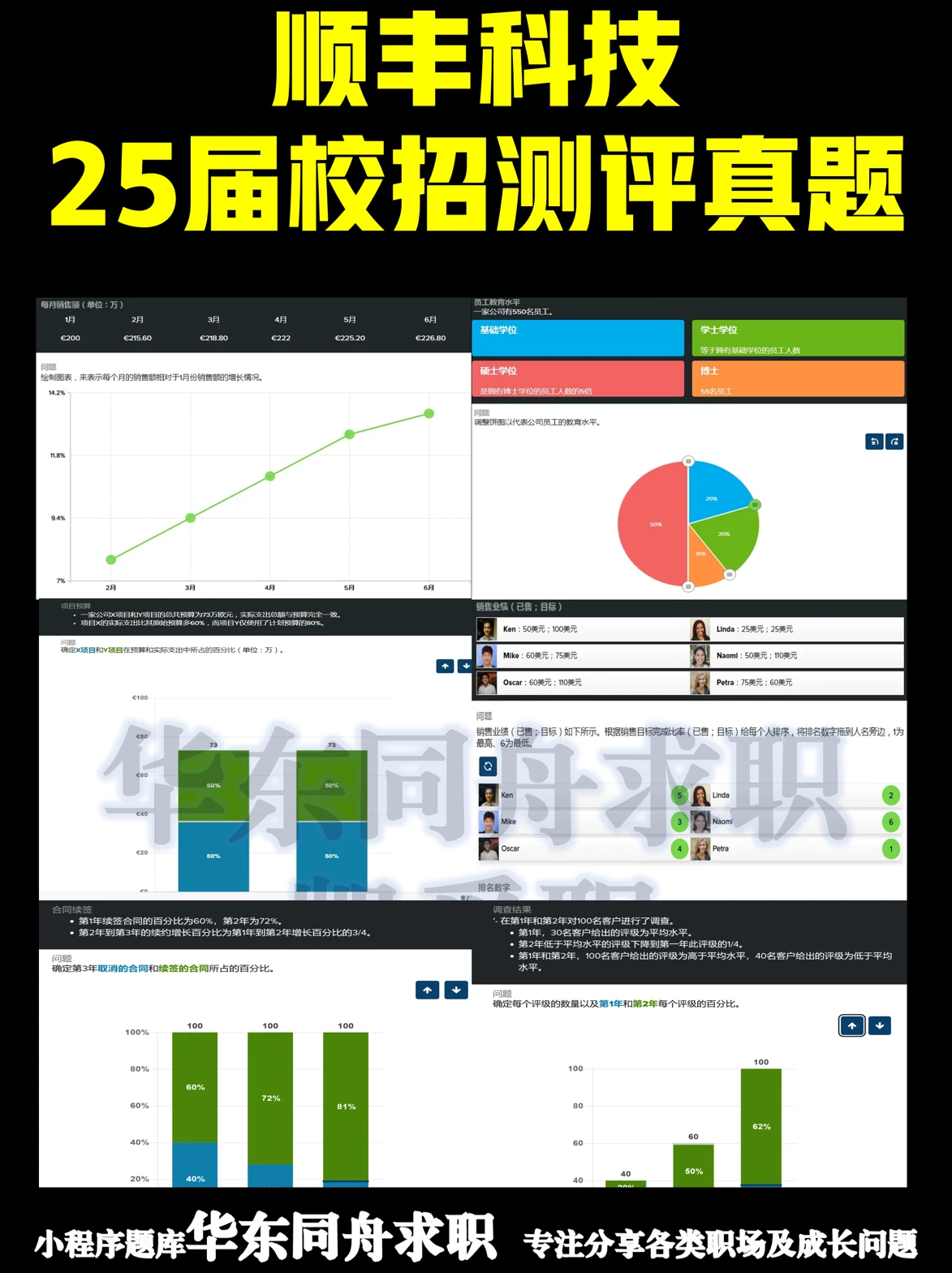
题意

$n$ 位同学站成一排，音乐老师要请其中的 $n-k$ 位同学出列，使得剩下的 $k$ 位同学排成合唱队形。

合唱队形是指这样的一种队形：设 $k$ 位同学从左到右依次编号为 $1,2,\dots ,k$，他们的身高分别为 $t_1,t_2,\dots ,t_k$ ，则他们的身高满足 $t_1<\cdots <t_i>t_{i+1}>t_k(1\le i\le k)$。

你的任务是，已知所有 $n$ 位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。

思路

题目其实就是要求 $k$ 最大。即在 $n$ 个数中找到 $k$ 个数，使得前半段单调递增，后半段单调递减。

记 $u{p}_i$ 表示以 $i$ 个数为结尾的最长上升子序列长度，则 $u{p}_i={\max }_{j=1}^{i}u{p}_j+1(a_i>a_j)$，同理可以处理 $dow{n}_i$。则要想让 $k$ 最大，就是让 $u{p}_i+dow{n}_i$ 最大，找到最大的 $u{p}_i+dow{n}_i$，$k=u{p}_i+dow{n}_i-1$。（第 $i$ 个点被统计两次），最后别忘了输出的是 $n-k$。

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,a[105],up[105],down[105];
signed main() {
	scanf("%lld",&n);
	for(int i = 1;i <= n;i++) scanf("%lld",&a[i]);
	for(int i = 1;i <= n;i++) {
		up[i] = 1;
		for(int j = 1;j < i;j++) {
			if(a[j] < a[i]) up[i] = max(up[i],up[j] + 1);
		}
	}
	for(int i = n;i >= 1;i--) {
		down[i] = 1;
		for(int j = n;j > i;j--) {
			if(a[j] < a[i]) down[i] = max(down[i],down[j] + 1);
		}
	}
	int ans = -1e18;
	for(int i = 1;i <= n;i++) ans = max(ans,up[i] + down[i] - 1);
	printf("%lld\n",n - ans);
    return 0;
}