Dijikstra算法（堆优化版）

news2024/11/15 23:53:57

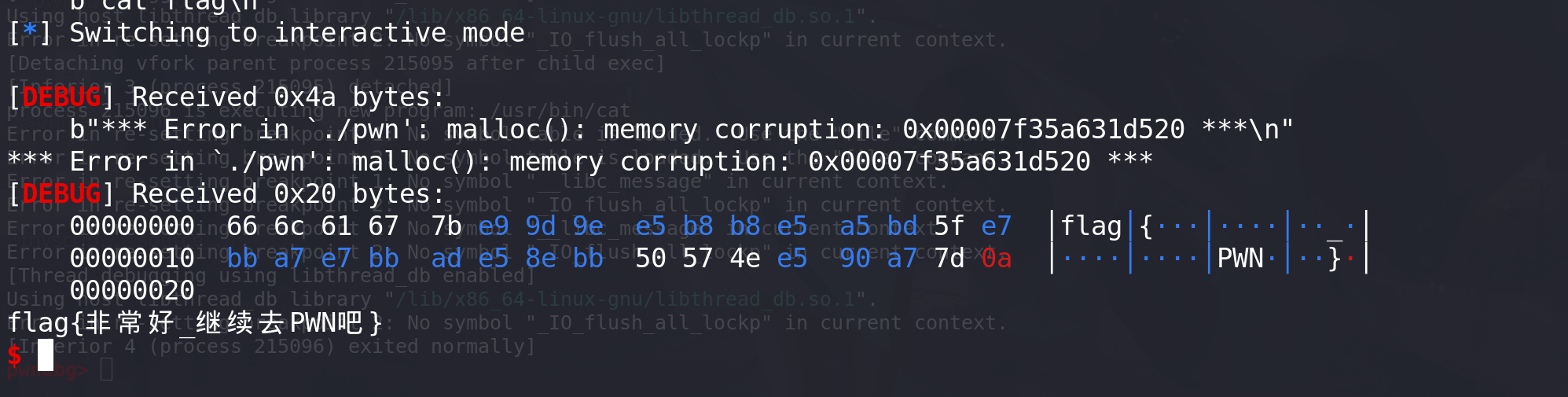
当给定数据的范围不大时，采用朴素Dijikstra算法尚能ac，但若是数据范围大于10^5，那么朴素Dijikstra算法就会爆掉，所以我们需要采用堆优化版的Dijikstra算法

堆优化版Dijikstra主要是对朴素Dijikstra中找寻从距离编号 1 结点路径长度最近的结点的过程进行了优化：

朴素Dijikstra算法：

int t = -1;
for (int j = 1;j<= n;++j)
{
    if(!st[j] && ( t == -1 || dist[t] > dist[j]))
        t = j;
}

这段代码的详解请看

http://t.csdnimg.cn/4eT8Z

题目如下：

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环，所有边权均为非负值。

请你求出 1 号点到 n 号点的最短距离，如果无法从 1 号点走到 n 号点，则输出 −1。

输入格式

第一行包含整数 n 和 m。

接下来 m 行每行包含三个整数 x,y,z，表示存在一条从点 x 到点 y 的有向边，边长为 z。

输出格式

输出一个整数，表示 1 号点到 n 号点的最短距离。

如果路径不存在，则输出 −1。

数据范围

1≤n,m≤1.5×10^5

解答代码：

#include<iostream>
#include<cstring>
#include<queue>

using namespace std;

typedef pair<int ,int> pii;//这是队列中的数据类型
                           //{x,y}代表的就是从源节点到编号为 y 的结点的最短路径长是 x 

const int N = 150010;

int n,m;
int e[N],ne[N],h[N],idx,w[N];//用邻接表存储图，因为本题中，结点数的范围和边的范围差不多
                             //本题图的形式是稀疏图，所以用邻接表
                             //邻接表适用于稀疏图，邻接矩阵适用于稠密图
                             //稠密图是边的个数的范围比结点个数的范围要大得多
                             //w[N]用来记录每一条边的边的长度，其中的N是结点的下标
int dist[N];//如dist[i]，从编号 1 结点到编号 i 结点的最短路径长度
bool st[N];//如st[i]，编号 i 结点是否被确定最短路径


void add(int a,int b,int c)
{
    e[idx] = b;
    w[idx] = c;
    ne[idx]=  h[a];
    h[a] = idx;
    idx++;
}

int dijikstra()
{
    memset(dist,0x3f,sizeof(dist));//还是将dist数组初始值设为无穷大
                                   //即最开始时，任何一个点的最短路径长度都还没确定
                                   //除了dist[1] = 0 ，也就是编号 1 结点到自身的距离为0
    dist[1] = 0;
    
    priority_queue<pii,vector<pii>,greater<pii>> heap;//采用优先队列实现小根堆排序
                                                      //优先队列的本质就是小根堆
    heap.push({0,1});//此时已知从编号 1 结点到编号 1 结点的最短路径长是0
    
    while(heap.size())
    {
        pii t = heap.top();//取出堆顶的元素
                           //优先队列中的所有pair数据的排序默认按照pair中的第一个数据进行排序
                           //优先队列模仿的是小根堆
                           //也就是堆顶的元素永远是此时距离编号 1 结点最近的编号
        heap.pop();//弹出堆顶元素
        
        int ver = t.second;//ver代表堆顶结点的编号
        int distance = t.first;//distance代表从编号 1 结点到堆顶结点的最短路径长度
        
        if(st[ver])//处理遇到重边的情况，画图
        continue;
        
        st[ver] = true;//标记这个点已经找到了最短路径
        
        for (int i = h[ver];i != -1;i = ne[i])//在此时的堆顶结点进行延伸
                                              //此时的 i 是编号 ver 结点的一个子节点的下标
        {
            int j =e[i];//将下标 i 翻译成结点的编号
            
            if (dist[j] > (distance + w[i]))//（1）确定从编号1结点到编号j结点的最短路径长
                                            //（2）处理重边的情况
            {
                dist[j] = distance + w[i];
                heap.push({dist[j],j});//加入队列
                                       //同时依照队列排序的特性，可以处理遇到重边的情况
            }
        }
    }
    
    if  (dist[n] == 0x3f3f3f3f)
    return -1;
    
    else
    return dist[n];
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    
    cin >> n >> m;
    memset(h,-1,sizeof(h));//照例将存储邻接表的h数组初始值设为-1
                           //代表初始时，图中任何一条边还没有建立
                           
    while(m--)
    {
        int a,b,c;
        cin >> a >> b >>c;
        
        add(a,b,c);
    }
    
    cout << dijikstra()  ;
    return 0;
}

几个问题：