第十四章 概率图模型

概率图模型分类

• 第一类使用有向无环图表示变量之间的因果关系，称为有向图模型或贝叶斯网络；

• 另一类使用无向图表示变量之间的相关关系，称为无向图模型或马尔可夫网，马尔可夫随机场。

14.1 隐马尔可夫模型

贝叶斯网络

在一个贝叶斯网络中：

• 节点表示一个或一组随机变量
• 边表示变量之间的依赖关系

一种图模型，表示随机变量之间的概率关系。每个节点都与一个概率分布相关，该分布描述了给定其父节点值时该节点的条件概率分布。

马尔科夫链

定义：描述了在一系列离散事件中，从一个状态转移到另一个状态的过程。

马尔可夫性：当前时刻的状态只依赖于前一时刻的状态，与更久的状态无关。

隐马尔科夫模型

**隐马尔可夫模型($HMM$)**是统计模型，它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析，例如模式识别。

14.2 马尔可夫随机场($MRF$)

定义：具有马尔可夫属性的随机变量的集合，由一个无向图来描述。

核心：处理的是联合概率。

马尔可夫场定理

马尔科夫随机场的理论基石是马尔科夫场定理，它描述了一个随机变量集合中，若任意一个变量的条件概率仅依赖于其相邻节点的取值（局部马尔科夫性），则该集合构成一个马尔科夫随机场。

算法原理

马尔科夫随机场的核心算法主要包括概率推理和参数学习两部分。

概率推理

主要解决给定模型参数下，求解数据观测值对应的潜在变量分布或边缘概率的问题。常见的概率推理方法包括精确推理（如信念传播、变分推理）和近似推理（如MCMC采样、Loopy Belief Propagation）。这些方法利用马尔科夫随机场的局部马尔科夫性和无向图结构，通过消息传递、能量最小化或采样技术来估计模型的后验概率分布。

参数学习

目的是从观测数据中学习马尔科夫随机场的参数，如势函数或因子权重。常用的参数学习算法包括最大似然估计、最大后验概率估计、变分贝叶斯方法等。这些方法通常涉及优化问题的求解，如梯度下降、牛顿法、EM算法等，以最大化模型对观测数据的拟合度。

算法对比

与朴素贝叶斯对比：朴素贝叶斯假设特征之间相互独立，而马尔科夫随机场允许建模特征间的依赖关系，因此在处理具有复杂关联的数据时，马尔科夫随机场通常能获得更好的性能。

与深度学习对比：深度学习模型如卷积神经网络（CNN）在图像处理等领域展现出强大能力，但其黑箱特性限制了模型解释性。相比之下，马尔科夫随机场通过显式建模变量间的依赖关系，具有更好的可解释性。然而，深度学习模型在大量标注数据的支持下，可能在某些任务上达到更高的精度。

14.3 条件随机场($CRF$)

核心：处理的是条件概率

条件随机场是一种用于序列标注（sequence labeling）的概率模型。它是马尔可夫随机场的一种扩展，可以用无向图来表示输入序列和输出序列之间的条件依赖关系。条件随机场的每个节点对应一个输出标签，每条无向边表示两个相邻标签之间的相关性，每个节点的概率分布由输入序列和相邻节点的取值共同决定。

优缺点

优点

• 利用丰富的特征来描述输入序列和输出序列之间的复杂关系，而不受马尔可夫假设的限制。

• 在全局范围内对输出序列进行建模，而不是局部地对每个输出标签进行建模，从而避免了标注偏置问题。

• 通过无向图来表示输出序列的依赖结构，而不是有向图，从而避免了循环依赖问题。

缺点

• 训练和预测过程都比较耗时(特别是当特征的个数和标签的个数很大时，计算归一化因子和最优序列的代价很高)。

• 特征选择和权重调整都需要人工干预，没有自动化的方法来确定最优的特征组合和权重分配。

• 模型参数和特征函数都是固定的，不能随着数据的变化而自适应地更新和调整。

链式条件随机场

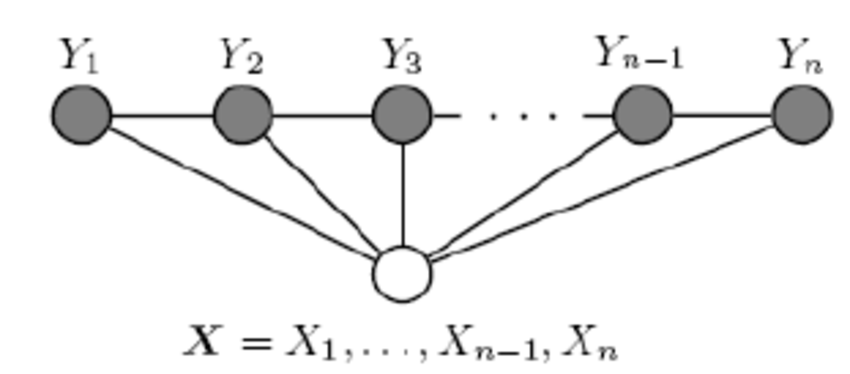
在CRF的定义中，我们并没有要求XX和YY有相同的结构。而实现中，我们一般都假设$X$和$Y$有相同的结构，即:$X=(X1,X2,...Xn),Y=(Y1,Y2,...Yn)$。$X$和$Y$有相同的结构的$CRF$就构成了线性链条件随机场($linear-CRF$)。

14.4 学习与推断

对于生成式模型，通常我们都是先对变量的联合概率分布进行建模，接着再求出目标变量的边际分布。

从联合概率得到边际分布，使用的是学习与推断。

变量消去

变量消去利用条件独立性来消减计算目标概率值所需的计算量，它通过运用乘法与加法的分配率，将对变量的积的求和问题转化为对部分变量交替进行求积与求和的问题，从而将每次的运算控制在局部，达到简化运算的目的。

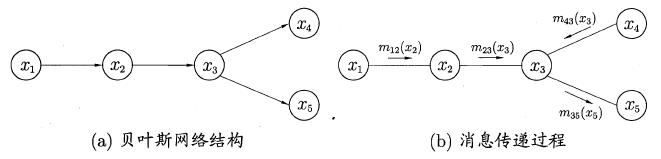
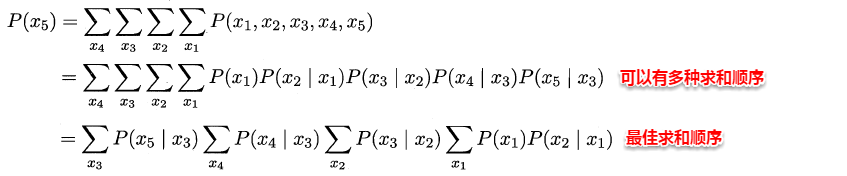
信念传播

若将变量求和操作看作是一种消息的传递过程，信念传播可以理解成：一个节点在接收到所有其它节点的消息后才向另一个节点发送消息，同时当前节点的边际概率正比于他所接收的消息的乘积：

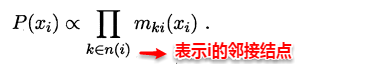
因此只需要经过下面两个步骤，便可以完成所有的消息传递过程。利用动态规划法的思想记录传递过程中的所有消息，当计算某个结点的边际概率分布时，只需直接取出传到该结点的消息即可，从而避免了计算多个边际分布时的冗余计算问题。

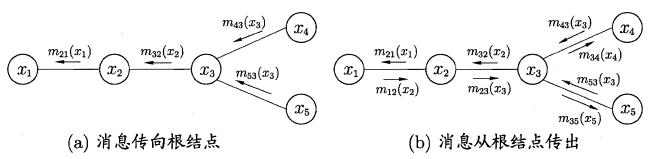
• 指定一个根节点，从所有的叶节点开始向根节点传递消息，直到根节点收到所有邻接结点的消息**（从叶到根）**；
• 从根节点开始向叶节点传递消息，直到所有叶节点均收到消息**（从根到叶）**。
• 

14.5 近似推断

精确推断方法计算开销大，因此在现实应用中近似推断方法更为常用。

近似推断方法大致可以分为两类：

• 采样法：通过使用随机化方法完成近似，如$MCMC$采样；

• 变分推断：使用确定性近似完成推断。

$MCMC$采样

采样是为了评估一个函数在某个分布上的期望值。

$MCMC$采样方法：先设法构造一条马尔可夫链?使其收敛至平稳分布 恰为待估计参数的后验分布?然后通过这条马尔可夫链来产生符合后验分布的 样本，并基于这些样本来进行估计。

$MCMC$方法的关键就在于通过构造"平稳分布为p的马尔同夫链" 来产生样本：若马尔可夫链运行时间足够长(即收敛到平稳状态)，则此时产出 的样本x近似服从于分布p 。

变分推断

变分推断通过使用已知简单分布来逼近需推断的复杂分布，并通过限制近似分布的类型，从而得到

一种局部最优、但具有确定解的近似后验分布。

14.6 话题模型

话题模型是一类生成式有向图模型，主要用来处理离散型的数据集合（如文本集合）。其中隐狄利克雷分配模型（$LDA$）是话题模型的杰出代表。在话题模型中，有以下几个基本概念：词、文档、话题。

词：最基本的离散单元；
文档：由一组词组成，词在文档中不计顺序；
话题：由一组特定的词组成，这组词具有较强的相关关系。
在现实任务中，一般我们可以得出一个文档的词频分布，但不知道该文档对应着哪些话题，LDA话题模型正是为了解决这个问题。具体来说：LDA认为每篇文档包含多个话题，且其中每一个词都对应着一个话题。因此可以假设文档是通过如下方式生成：

这样一个文档中的所有词都可以认为是通过话题模型来生成的，当已知一个文档的词频分布后（即一个N维向量，N为词库大小），则可以认为：每一个词频元素都对应着一个话题，而话题对应的词频分布则影响着该词频元素的大小。