基于二叉树的近似最近邻搜索-Annoy

在推荐系统的召回阶段，会实时计算用户的表征向量（user/query），然后去物料库去寻找与用户最匹配的N个物料返回给用户；
在搜索系统，也同样存在这样的需求，用户的搜素（query）转化为向量，然后去文档库中搜索最相似的N个文档进行返回；
再比如如今火热的LLM（大语言模型）中的一个分支-RAG（检索增强生成），也是将用户输入（query）转化为语义向量，然后去向量数据库中召回最相关的N个文档作为上下文补充；

再比如人脸识别、相似图片搜索等等，诸如此类的场景，最朴素（暴力）的做法是遍历所有备选数据，与query逐一进行比较，计算向量的相关性，得到最相关的Top-N个备选项，时间复杂度为O(n)。但在工业场景中，备选数据集往往是非常庞大，这种做法明显不符合要求。

因此，便有了今天的主题：Approximate Nearest Neighbors Search（近似最近邻搜索） ，它可以在牺牲一定精度的前提下，大大提升这个搜索过程的速度，这也是工业采用的普遍做法。

近似最近邻搜索目前是有多种实现算法的，这篇文章介绍其中一种基于二叉树的算法：Annoy（Approximate Nearest Neighbors Oh Yeah）

原理解析

annoy的目标是能够以 O(log n) 的时间复杂度来实现最近邻的搜索，使用了二叉树的数据结构。

下面，便于演示和理解，以二维向量的数据集为例进行分析，正式开始整个原理的解析。

二叉树构建

首先，从数据集中随机选择两个点，然后用这两个点的等距超平面（在二维中便是垂直平分线/中垂线），去将数据集切分为两部分。如下图，灰色的线连接的两个点，黑色的粗线对应中垂线，将整个数据集切分为绿色和蓝色两部分。

接着，分别对两个子空间进行同样的操作，如下图，这样就可以得到四个空间。

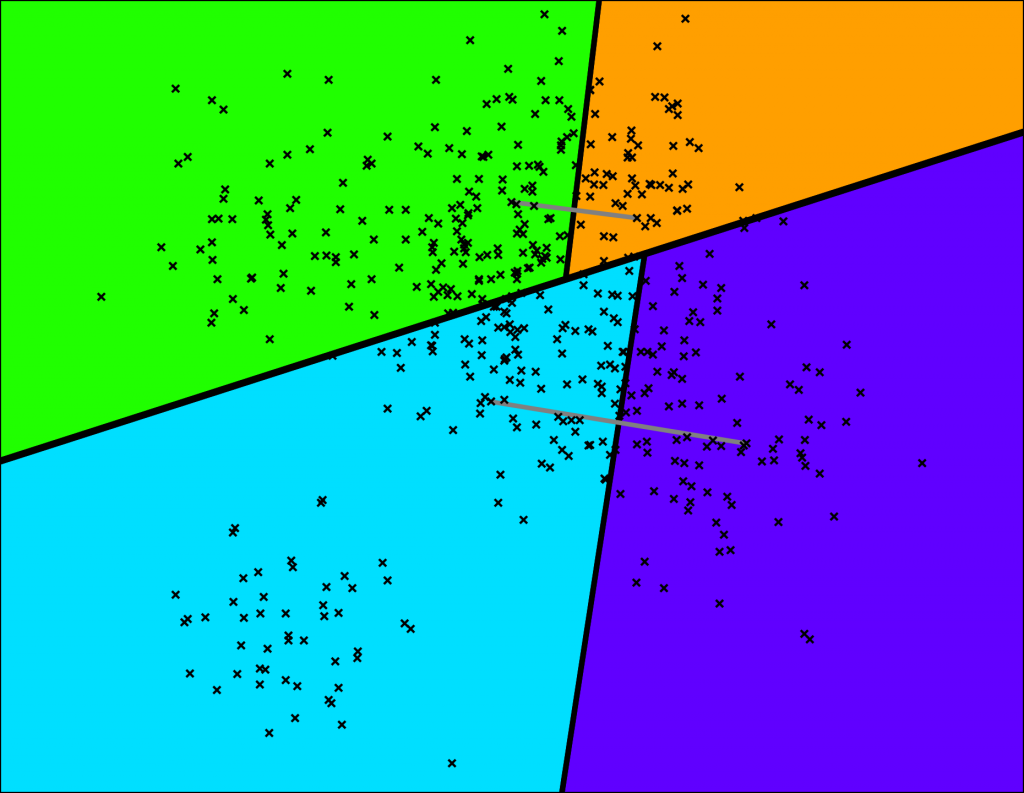
以二叉树的结构来表示，所有数据点只存储在叶子节点，比如下图，橙色的叶子节点存储了60个点：

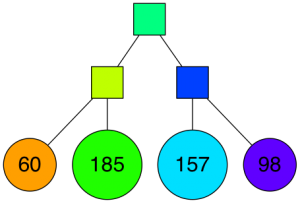
下面便是递归地持续进行同样的操作，直到每个节点/空间最多只有K个点

比如下图，便是K=10的最终划分结果：

K=10

其对应的二叉树结构如下：

二叉树-K=10

这样，我们就得到了一棵将原来的数据点划分成多个空间的二叉树。并且，巧妙的是那些在同一个空间的所有点之间，会比在其他空间的点更有可能是更相近的换句话说，两个相近的点是不太可能会被分开的。

搜索过程

那么，完整地构建了这棵二叉树之后，对于任意一个点，或者来一个新的数据点，如何找到与其最相近的N个点便成了关键。

首先，从二叉树的根节点开始遍历。每一个中间节点（分支节点）都对应一个上述的超平面
根据这个超平面，判断是往左子节点还是右子节点继续往下遍历
直到遍历到叶子节点，便结束搜索过程，叶子节点存储的所有点都是在同一个子空间的，更大可能是与之相近的点。

空间遍历

二叉树遍历

比如上图[空间遍历]，红色的点X最终划分到了浅蓝色的子空间，便是最终搜索得到的7个最近邻点。对应二叉树的遍历路径则对应上图[二叉树遍历]。

这个过程的时间复杂度是O(log n)，因为它的搜索遍历是二叉树的深度。

存在问题

进一步分析，上面的搜索过程是可能存在以下两个问题的：

如果我们想要超过7个的最近邻点呢
一些更加相近的点是存在于叶子节点之外的，即可能不在同一个子空间

（上述也提到了两个相近的点是不太可能会被分开的，但这仅仅只是可能性低，符合大部分的数据点）

针对这两个问题，annoy采用了两个技巧来应对。

技巧1

在遍历二叉树的过程中，两个方向/左右子树如果"足够相近"，那么会同时沿着两个方向进行遍历，而不是只往一个方向进行遍历。

如下图，最终可以进入到多个子空间：

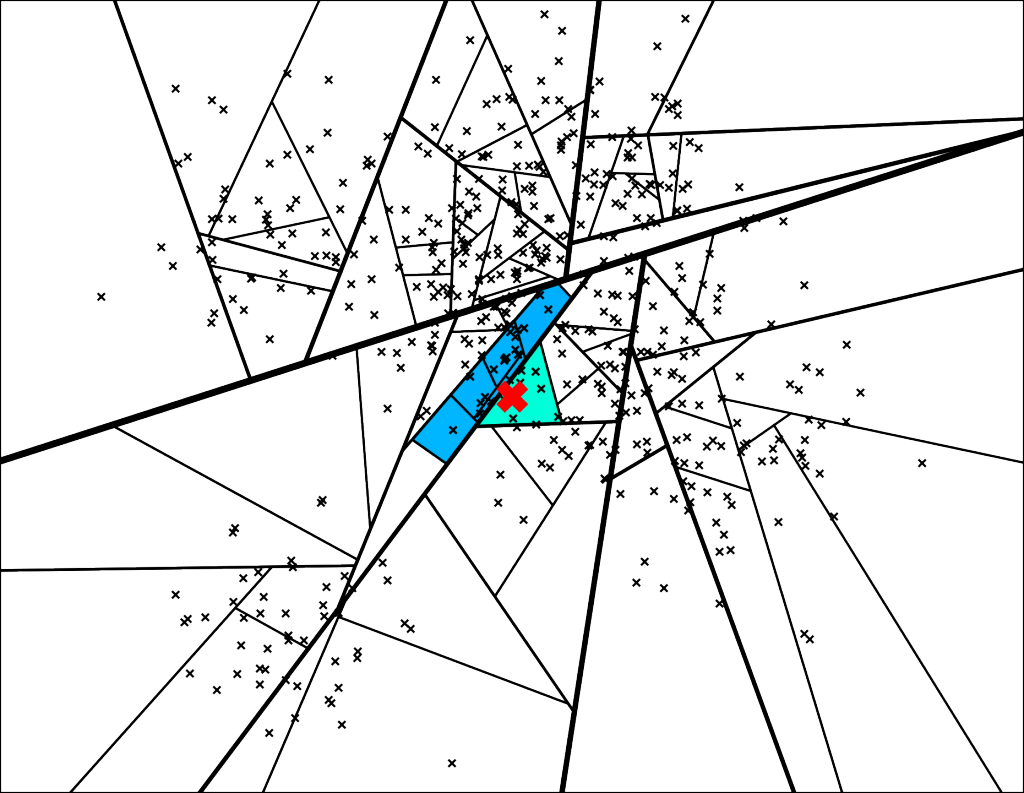
对应的二叉树遍历路径：

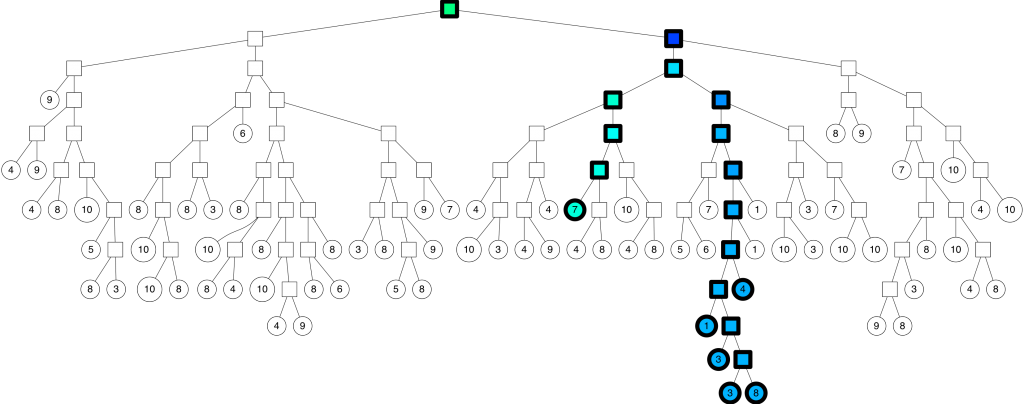
那么，这个“足够相近”需要有一个量化的东西，这里可以定义一个距离阈值（与超平面的距离），如果小于这个阈值，那么就同时沿着“错误”的另外一边进行遍历。比如上一个小节没有用到这个阈值判断，也即等同于阈值=0，总是只往着“正确”的一边进行遍历，得到了7个最近邻点。而当阈值=0.5时，便对应了上图的遍历路径，能够得到26个最近邻点（7+4+1+3+3+8）

而真正的技巧在于如何使用这个阈值：

使用一个优先队列放入按照与超平面的距离进行排序的“错误”节点，这样便可以从距离最近->距离较远的“错误”节点去遍历，直到超过指定阈值。

技巧2

类似于机器学习中的随机森林，annoy使用的第2个技巧便是同样的思路：构建多棵二叉树，由于每次划分子空间时是随机选取的点，因此这些二叉树是不同的。

创建一个优先队列，对构建的所有二叉树使用上述的方法进行搜索遍历，那么每一棵树都能得到一个叶子节点，这些叶子节点存储了与query point更高可能性相近的点，即质量很好的预估最邻近点

比如下面两张图，不同的二叉树可以搜索遍历得到不同的叶子节点/子空间：

二叉树-1

二叉树-2

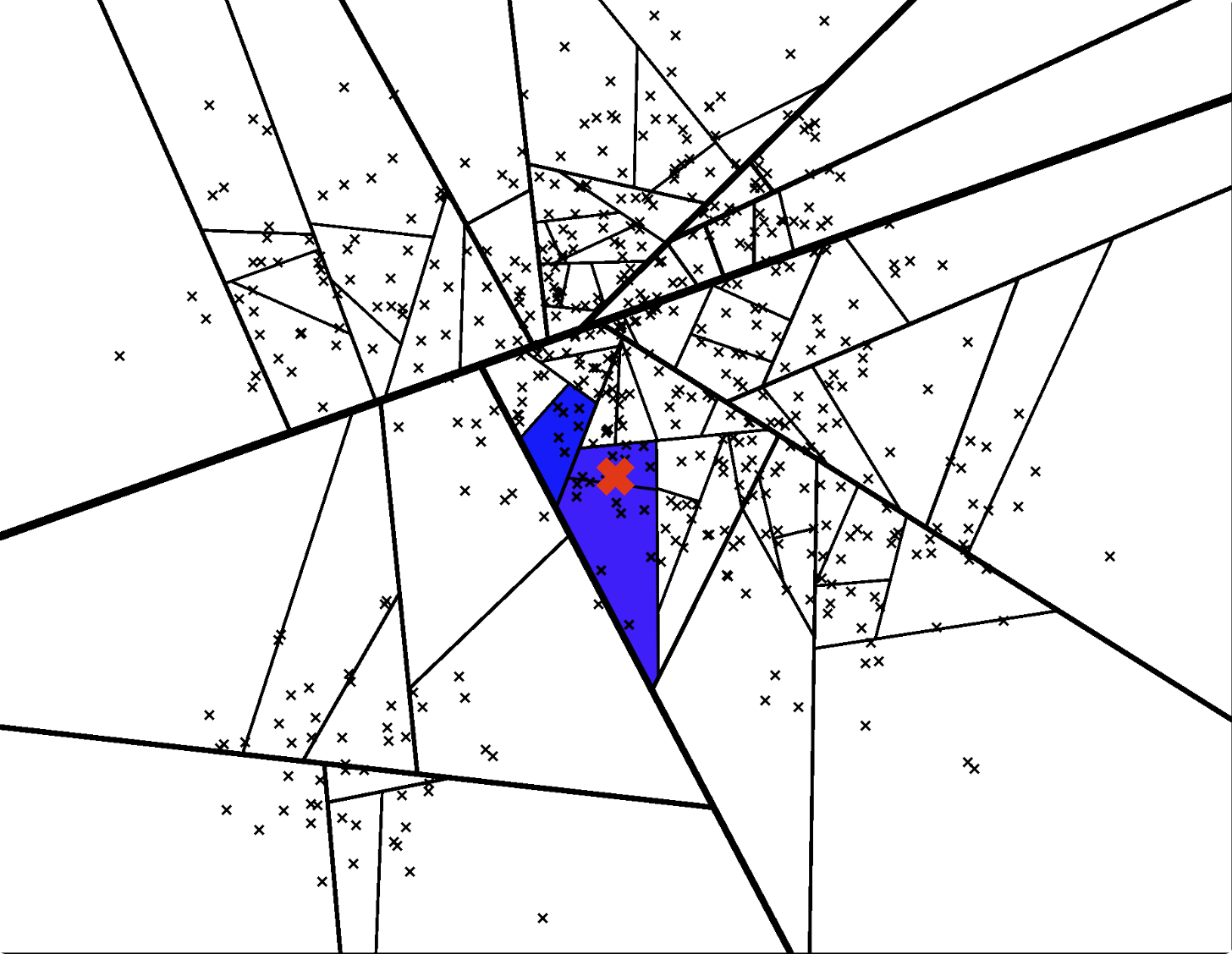
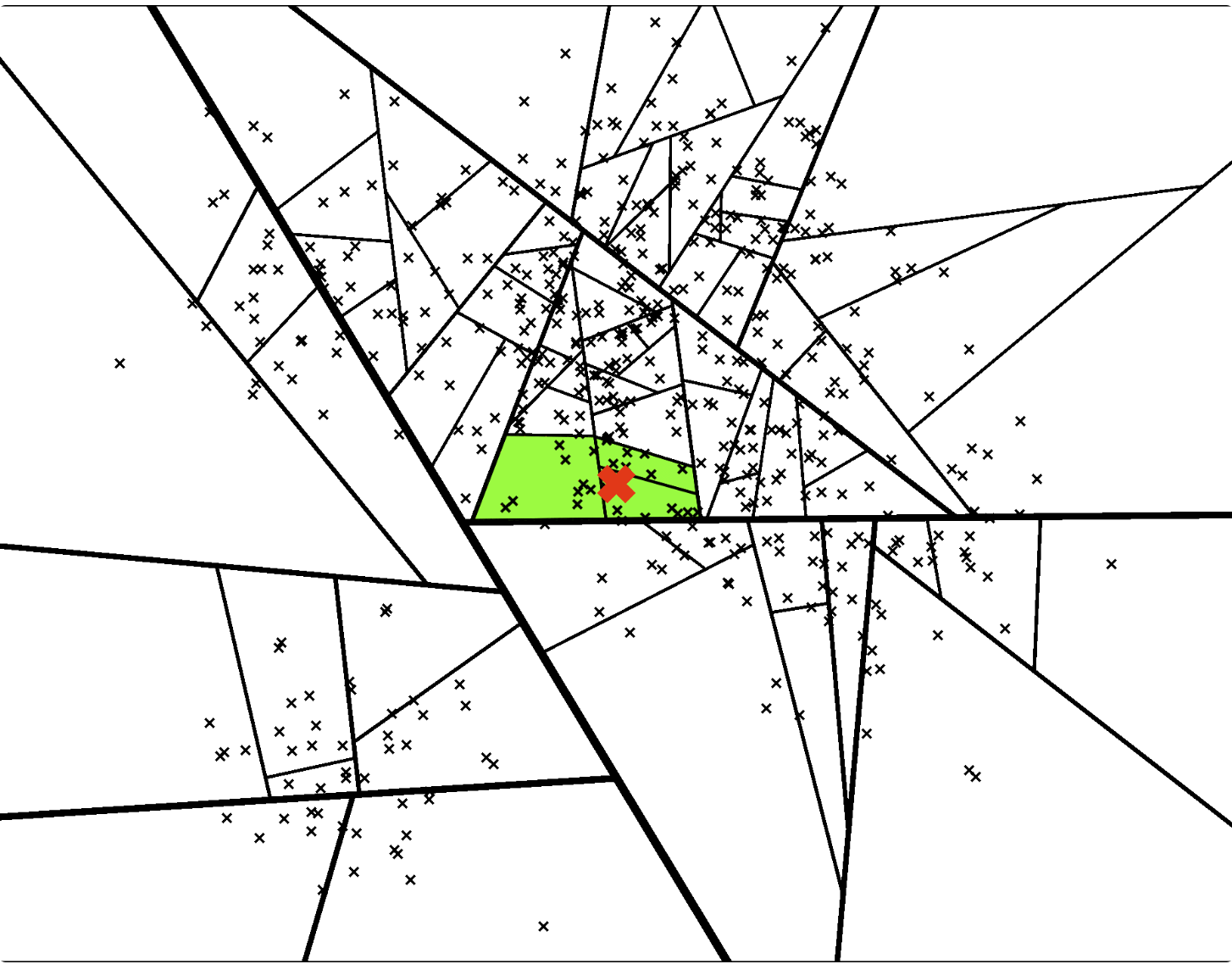
那么，这样我们就得到一个叶子节点的集合，在整个数据点空间可以表示为如下图：

到了最后一步，可以将这个集合缩小一下。可以注意到，到目前为止，甚至完全没有出现过与每一个点的距离计算，那么这一步便是query point与集合里面的所有点一一进行距离的计算，然后进行排序，得到距离最近的Top N个点。

不过，从下图可以看出，仍然存在小部分的点会被排除在外，这是无法百分百避免，因为这是一个“近似”最近邻搜索，有小小的精度损失是可以接受的，但这可以带来极大的性能提升，比如我们仅仅需要与1%的点进行距离计算，这便可以带来100倍的性能提升，与暴力搜索相比。

算法总结

预处理阶段：

构建一堆二叉树，对于每一棵树，都是递归的进行随机空间划分

搜索阶段：

将每一棵树的根节点加入优先队列
使用这个队列，对所有二叉树进行搜索遍历，直到我们得到了search_k个备选的最近邻点；
移除重复的点
与所有备选的点进行一一距离计算
根据距离进行排序
返回距离最近的Top N个点

到这里，整个annoy的算法原理便全部介绍完毕了。里面有两个关键的参数：构建的二叉树的数量-n_trees和搜索的最近邻点的备选数量search_k，用于平衡搜索性能和搜索精度的，更大的n_trees和search_k可以得到更高的精度，但同时会带来更多的预处理和搜索耗时。

annoy实践

安装

pip install fastannoy

github: fastannoy

api介绍

AnnoyIndex(f, metric)：返回一个可读写的新索引, 并存储f维的向量。度量可以是"angular", “euclidean”, “manhattan”, “hamming”, or “dot”。
a.add_item(i, v)：将项i(任何非负整数)与向量v相加。请注意, 它将为max(i)+1项分配内存。
a.build(n_trees, n_jobs=-1)：构建n棵树的森林。更多的树在查询时具有更高的精度。调用build后, 无法添加更多项目。njobs指定用于构建树的线程数。n_jobs=-1使用所有可用的CPU内核。
a.save(fn, preful=False)：将索引保存到磁盘并加载(请参阅下一个函数)。保存后, 无法添加更多项目。
a.load(fn, preful=False)：从磁盘加载(mmaps)索引。如果preful设置为True, 它将把整个文件预读入内存(使用mmap和MAP_POPULATE)。默认值为False。
a.unload()：卸载。
a.get_nns_by_item(i, n, search_k=-1, include_ranges=False)：返回n个最接近的项。在查询过程中, 它将检查最多search_k个节点, 如果没有提供, 则默认为n_trees*n。search_k为您提供了更好的准确性和速度之间的运行时权衡。如果你将include_ranges设置为True, 它将返回一个包含两个列表的2元素元组：第二个列表包含所有相应的距离。
a.get_nns_by_vector(items, n, search_k=-1, include_densives=False)：相同, 但按向量v查询。
get_batch_nns_by_items(vectors, n, search_k=-1, include_densives=False)： get_nns_by_item 的批量查询版本。
a.get_nns_by_vector(v, n, search_k=-1, include_densives=False)： get_nns_by_vector 的批量查询版本。
a.get_item_vector(i)：返回之前添加的项i的向量。
a.get_distance(i, j)：返回项目i和j之间的距离。注意：这用于返回距离的平方, 但自2016年8月起已更改。
a.get_n_items()：返回索引中的项目数。
a.get_n_trees()：返回索引中的树数。
a.on_disk_build(fn)：准备在指定文件而不是RAM中构建索引(在添加项之前执行, 构建后无需保存)
a.set_sed(seed)：将使用给定的种子初始化随机数生成器。仅用于构建树, 即只需在添加项目之前通过此项。调用a.build(n_trees)或a.load(fn)后将无效。

代码示例

from fastannoy import AnnoyIndex
import random

f = 40  # Length of item vector that will be indexed

t = AnnoyIndex(f, 'angular')
for i in range(1000):
    v = [random.gauss(0, 1) for _ in range(f)]
    t.add_item(i, v)

t.build(10) # 10 trees
t.save('test.ann')

# ...

u = AnnoyIndex(f, 'angular')
u.load('test.ann') # super fast, will just mmap the file
print(u.get_nns_by_item(0, 100)) # will find the 100 nearest neighbors
"""
[0, 17, 389, 90, 363, 482, ...]
"""

print(u.get_nns_by_vector([random.gauss(0, 1) for _ in range(f)], 100)) # will find the 100 nearest neighbors by vector
"""
[378, 664, 296, 409, 14, 618]
"""

批量查询

# will find the 100 nearest neighbors

print(u.get_batch_nns_by_items([0, 1, 2], 100))
"""
[[0, 146, 858, 64, 833, 350, 70, ...], 
[1, 205, 48, 396, 382, 149, 305, 125, ...], 
[2, 898, 503, 618, 23, 959, 244, 10, 445, ...]]
"""

print(u.get_batch_nns_by_vectors([
    [random.gauss(0, 1) for _ in range(f)]
    for _ in range(3)
], 100))
"""
[[862, 604, 495, 638, 3, 246, 778, 486, ...], 
[260, 722, 215, 709, 49, 248, 539, 126, 8, ...], 
[288, 764, 965, 320, 631, 505, 350, 821, 540, ...]]
"""