题目

给你一个由 正整数 组成、大小为 m x n 的矩阵 grid。你可以从矩阵中的任一单元格移动到另一个位于正下方或正右侧的任意单元格（不必相邻）。从值为 c1 的单元格移动到值为 c2 的单元格的得分为 c2 - c1 。

你可以从 任一 单元格开始，并且必须至少移动一次。

返回你能得到的 最大 总得分。

示例 1：

输入：grid = [[9,5,7,3],[8,9,6,1],[6,7,14,3],[2,5,3,1]]

输出：9

解释：从单元格 (0, 1) 开始，并执行以下移动：
- 从单元格 (0, 1) 移动到 (2, 1)，得分为 7 - 5 = 2 。
- 从单元格 (2, 1) 移动到 (2, 2)，得分为 14 - 7 = 7 。
总得分为 2 + 7 = 9 。

示例 2：

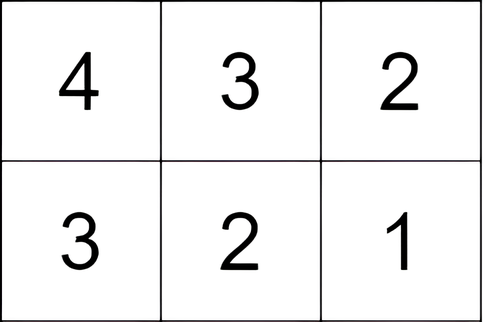
输入：grid = [[4,3,2],[3,2,1]]

输出：-1

解释：从单元格 (0, 0) 开始，执行一次移动：从 (0, 0) 到 (0, 1) 。得分为 3 - 4 = -1 。

提示：

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 1000
• 4 <= m * n <= 105
• 1 <= grid[i][j] <= 105

思路

二维前缀和

premin[i][j]表示(0,0)到(i,j)形成的矩形中最小的元素

pre表示当前元素左上方最小的元素

代码

class Solution {
    public int maxScore(List<List<Integer>> grid) {
        int m = grid.size(), n = grid.get(0).size();
        // premin[i][j]表示(0,0)到(i,j)形成的矩形中最小的元素
        int[][] premin = new int[m][n];
        for (int i = 0; i < m; i++) {
            Arrays.fill(premin[i], Integer.MAX_VALUE);
        }

        int ans = Integer.MIN_VALUE;

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                int pre = Integer.MAX_VALUE;
                if (i > 0) {
                    pre = Math.min(pre, premin[i - 1][j]);
                }
                if (j > 0) {
                    pre = Math.min(pre, premin[i][j - 1]);
                }
                // (0,0)不需要更新
                if (i + j > 0) {
                    ans = Math.max(ans, grid.get(i).get(j) - pre);
                }
                premin[i][j] = Math.min(pre, grid.get(i).get(j));
            }
        }
        return ans;
    }
}