目录
题目一:图像渲染
题目二:岛屿数量
题目三:岛屿的最大面积
题目四:被围绕的区域
题目五:太平洋大西洋水流问题
题目六:扫雷游戏
题目七:衣橱整理
题目一:图像渲染
有一幅以 m x n 的二维整数数组表示的图画 image ,其中 image[i][j] 表示该图画的像素值大小。
你也被给予三个整数 sr , sc 和 newColor 。你应该从像素 image[sr][sc] 开始对图像进行 上色填充 。
为了完成 上色工作 ,从初始像素开始,记录初始坐标的 上下左右四个方向上 像素值与初始坐标相同的相连像素点,接着再记录这四个方向上符合条件的像素点与他们对应 四个方向上 像素值与初始坐标相同的相连像素点,……,重复该过程。将所有有记录的像素点的颜色值改为 newColor 。
最后返回 经过上色渲染后的图像 。

输入: image = [[1,1,1],[1,1,0],[1,0,1]],sr = 1, sc = 1, newColor = 2 输出: [[2,2,2],[2,2,0],[2,0,1]] 解析: 在图像的正中间,(坐标(sr,sc)=(1,1)),在路径上所有符合条件的像素点的颜色都被更改成2。 注意,右下角的像素没有更改为2,因为它不是在上下左右四个方向上与初始点相连的像素点。
示例 2:
输入: image = [[0,0,0],[0,0,0]], sr = 0, sc = 0, newColor = 2 输出: [[2,2,2],[2,2,2]]
在bfs中做过这道题,直接看dfs的解法
从给定的位置,进行一次深度优先遍历即可
代码如下:
class Solution
{
int dx[4] = {0,0,-1,1};
int dy[4] = {-1,1,0,0};
int m, n, prev;
public:
vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color)
{
if(image[sr][sc] == color) return image;
m = image.size(), n = image[0].size();
prev = image[sr][sc];
dfs(image, sr, sc, color);
return image;
}
void dfs(vector<vector<int>>& image, int i, int j, int color)
{
image[i][j] = color;
for(int k = 0; k < 4; k++)
{
int x = i + dx[k];
int y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && image[x][y] == prev)
{
dfs(image, x, y, color);
}
}
}
};题目二:岛屿数量
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [ ["1","1","1","1","0"], ["1","1","0","1","0"], ["1","1","0","0","0"], ["0","0","0","0","0"] ] 输出:1
示例 2:
输入:grid = [ ["1","1","0","0","0"], ["1","1","0","0","0"], ["0","0","1","0","0"], ["0","0","0","1","1"] ] 输出:3
同样是在bfs那里做过的,与那里的思路基本相同,找到为 1 的岛屿后,深度优先遍历,直到找不到 1 位置,开始继续找下一个岛屿的位置,直到将数组遍历完为止
代码如下:
class Solution
{
typedef pair<int, int> PII;
// 判断数组,用于判断该位置是否被遍历过
bool vis[301][301];
int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0, 0};
// m、n定义为全局的,便于dfs函数能取到值
int m, n;
public:
int numIslands(vector<vector<char>>& grid)
{
int ret = 0;
m = grid.size(), n = grid[0].size();
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
if(grid[i][j] == '1' && !vis[i][j])
{
ret++;
dfs(grid, i, j);
}
}
}
return ret;
}
void dfs(vector<vector<char>>& grid, int i, int j)
{
vis[i][j] = true;
for(int k = 0; k < 4; k++)
{
int x = i + dx[k];
int y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == '1' && !vis[x][y])
{
dfs(grid, x, y);
}
}
}
};题目三:岛屿的最大面积
给你一个大小为 m x n 的二进制矩阵 grid 。
岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
岛屿的面积是岛上值为 1 的单元格的数目。
计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
示例 1:

输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]] 输出:6 解释:答案不应该是11,因为岛屿只能包含水平或垂直这四个方向上的1。
示例 2:
输入:grid = [[0,0,0,0,0,0,0,0]] 输出:0
此题同样是在bfs中做过
每次进入一个岛屿时,定义一个count,用于统计一个岛屿的面积,每次遍历完一个岛屿,比较岛屿的面积,得到岛屿的最大面积
在dfs函数中,每次都找当前位置的上下左右四个位置,如果这四个位置有满足条件的,就继续dfs,直到跳出dfs为止
代码如下:
class Solution
{
public:
typedef pair<int, int> PII;
// 判断数组,用于判断该位置是否被遍历过
bool vis[51][51];
int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0, 0};
// m、n定义为全局的,便于dfs函数能取到值
int m, n, count;
int maxAreaOfIsland(vector<vector<int>>& grid)
{
m = grid.size(), n = grid[0].size();
int ret = 0;
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
if(grid[i][j] == 1 && !vis[i][j])
{
count = 0;
dfs(grid, i, j);
ret = max(ret, count);
}
}
}
return ret;
}
void dfs(vector<vector<int>>& grid, int i, int j)
{
count++;
vis[i][j] = true;
for(int k = 0; k < 4; k++)
{
int x = i + dx[k];
int y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1 && !vis[x][y])
{
dfs(grid, x, y);
}
}
}
};题目四:被围绕的区域
给你一个 m x n 的矩阵 board ,由若干字符 'X' 和 'O' 组成,捕获 所有 被围绕的区域:
- 连接:一个单元格与水平或垂直方向上相邻的单元格连接。
- 区域:连接所有
'O'的单元格来形成一个区域。 - 围绕:如果您可以用
'X'单元格 连接这个区域,并且区域中没有任何单元格位于board边缘,则该区域被'X'单元格围绕。
通过将输入矩阵 board 中的所有 'O' 替换为 'X' 来 捕获被围绕的区域。
示例 1:
输入:board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出:[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释:
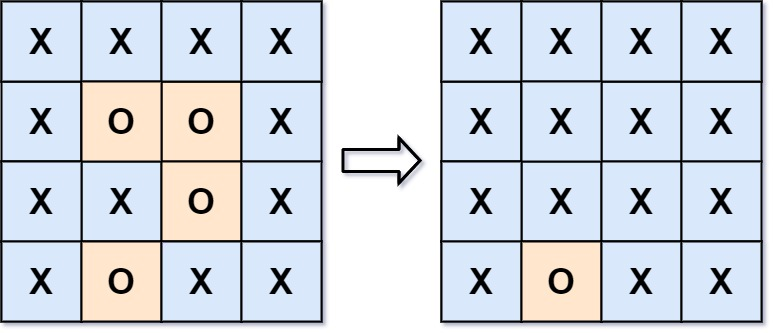
在上图中,底部的区域没有被捕获,因为它在 board 的边缘并且不能被围绕。
示例 2:
输入:board = [["X"]]
输出:[["X"]]
此题同样是在bfs中做过
正难则反,找被 X 包围的 O不好找,那就在最外圈,找没有被 X 包围的 O,将没有包围的先改为+,最后遍历一遍原数组,此时数组中的 O 就是被 X 包围的 O,将被包围的O改为X,最后再将刚刚没有被包围的+改为O
代码如下:
class Solution {
public:
typedef pair<int, int> PII;
// 判断数组,用于判断该位置是否被遍历过
int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0, 0};
// m、n定义为全局的,便于dfs函数能取到值
int m, n;
void solve(vector<vector<char>>& board)
{
m = board.size(), n = board[0].size();
for(int j = 0; j < n; j++)
{
if(board[0][j] == 'O') dfs(board, 0, j);
if(board[m - 1][j] == 'O') dfs(board, m - 1, j);
}
for(int i = 0; i < m; i++)
{
if(board[i][0] == 'O') dfs(board, i, 0);
if(board[i][n - 1] == 'O') dfs(board, i, n - 1);
}
for(int i = 0; i < m; i++)
for(int j = 0; j < n; j++)
{
if(board[i][j] == 'O') board[i][j] = 'X';
else if(board[i][j] == '+') board[i][j] = 'O';
}
}
void dfs(vector<vector<char>>& board, int i, int j)
{
board[i][j] = '+';
for(int k = 0; k < 4; k++)
{
int x = i + dx[k];
int y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'O')
{
dfs(board, x, y);
}
}
}
};题目五:太平洋大西洋水流问题
有一个 m × n 的矩形岛屿,与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界,而 “大西洋” 处于大陆的右边界和下边界。
这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights , heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。
岛上雨水较多,如果相邻单元格的高度 小于或等于 当前单元格的高度,雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。
返回网格坐标 result 的 2D 列表 ,其中 result[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。
示例 1:

输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]] 输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
示例 2:
输入: heights = [[2,1],[1,2]] 输出: [[0,0],[0,1],[1,0],[1,1]]
这道题的题意就是:
有一块陆地,左边和上面被太平洋包围,右边和下面被大西洋包围,矩阵中的数字代表高度,水可以从高的地方流到低的地方,如果高度相同也可以流动
题目求的就是,某一个位置的水既可以流向太平洋又可以流向大西洋,那就把这个位置的坐标存进vector中,最后返回
解法一:直接判断
找每一个位置,判断每一个位置是否能满足题意
这种解法是会超时的,因为某一个路径可能会重复计算进去,所以考虑解法二
解法二:正难则反
题目是求中间的位置是否能到太平洋和大西洋,那就转化为边界接触太平洋的位置,能否到大西洋;以及边界接触大西洋的位置,能否到太平洋
也就是如果靠近太平洋的坐标扩展到的位置,与靠近大西洋的坐标扩展到的位置重复了,就说明该位置,既能够流向太平洋又能够流向大西洋
而且解法二有一个优点,某一个位置能到达的地方,不会重复计算,因为在到达该位置时会记录下来,下一次不会走这个位置
需要两个vis数组,分别标记从太平洋和大西洋扩展到的位置,最后计算完毕后,统计扩展后重复的位置,存入ret中返回即可
代码如下:
class Solution
{
public:
int dx[4] = {0,0,-1,1};
int dy[4] = {-1,1,0,0};
vector<vector<int>> ret;
int m, n;
vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights)
{
m = heights.size(), n = heights[0].size();
vector<vector<bool>> vis1(m, vector<bool>(n));
vector<vector<bool>> vis2(m, vector<bool>(n));
// 太平洋
for(int j = 0; j < n; j++) dfs(heights, vis1, 0, j);
for(int i = 0; i < m; i++) dfs(heights, vis1, i, 0);
// 大西洋
for(int j = 0; j < n; j++) dfs(heights, vis2, m - 1, j);
for(int i = 0; i < m; i++) dfs(heights, vis2, i, n - 1);
// 如果vis1和vis2都标记为true,那就满足题意
for(int i = 0; i < m; i++)
for(int j = 0; j < n; j++)
if(vis1[i][j] == true && vis2[i][j] == true)
ret.push_back({i, j});
return ret;
}
void dfs(vector<vector<int>>& h, vector<vector<bool>>& vis, int i, int j)
{
vis[i][j] = true;
for(int k = 0; k < 4; k++)
{
int x = i + dx[k];
int y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && h[x][y] >= h[i][j] && !vis[x][y])
{
dfs(h, vis, x, y);
}
}
}
};题目六:扫雷游戏
让我们一起来玩扫雷游戏!
给你一个大小为 m x n 二维字符矩阵 board ,表示扫雷游戏的盘面,其中:
'M'代表一个 未挖出的 地雷,'E'代表一个 未挖出的 空方块,'B'代表没有相邻(上,下,左,右,和所有4个对角线)地雷的 已挖出的 空白方块,- 数字(
'1'到'8')表示有多少地雷与这块 已挖出的 方块相邻, 'X'则表示一个 已挖出的 地雷。
给你一个整数数组 click ,其中 click = [clickr, clickc] 表示在所有 未挖出的 方块('M' 或者 'E')中的下一个点击位置(clickr 是行下标,clickc 是列下标)。
根据以下规则,返回相应位置被点击后对应的盘面:
- 如果一个地雷(
'M')被挖出,游戏就结束了- 把它改为'X'。 - 如果一个 没有相邻地雷 的空方块(
'E')被挖出,修改它为('B'),并且所有和其相邻的 未挖出 方块都应该被递归地揭露。 - 如果一个 至少与一个地雷相邻 的空方块(
'E')被挖出,修改它为数字('1'到'8'),表示相邻地雷的数量。 - 如果在此次点击中,若无更多方块可被揭露,则返回盘面。
示例 1:

输入:board = [["E","E","E","E","E"],["E","E","M","E","E"],["E","E","E","E","E"],["E","E","E","E","E"]], click = [3,0] 输出:[["B","1","E","1","B"],["B","1","M","1","B"],["B","1","1","1","B"],["B","B","B","B","B"]]
示例 2:

输入:board = [["B","1","E","1","B"],["B","1","M","1","B"],["B","1","1","1","B"],["B","B","B","B","B"]], click = [1,2] 输出:[["B","1","E","1","B"],["B","1","X","1","B"],["B","1","1","1","B"],["B","B","B","B","B"]]
这道题其实就是我们平时在电脑上玩的扫雷游戏,规则是一样的
如果点击的是空方格,修改为B,同时就把周围一圈的方格全部打开,如果打开的方格中,周围有地雷,就修改为周围的地雷个数
接着再递归进入新打开的这些方格,如果依旧是空方格,就继续修改为B,再打开该方格周围一圈的方格
所以上述过程就是一个经典的dfs,与以往不同的是,dx和dy需要再加四个值,此时扩展的范围变为了8个,不再是上下左右4个了
代码如下:
class Solution
{
public:
int dx[8] = {0,0,-1,1,-1,-1,1,1};
int dy[8] = {-1,1,0,0,-1,1,-1,1};
int m, n;
vector<vector<char>> updateBoard(vector<vector<char>>& board, vector<int>& click)
{
// 直接点到地雷,直接返回
int x = click[0], y = click[1];
if(board[x][y] == 'M')
{
board[x][y] = 'X';
return board;
}
m = board.size(), n = board[0].size();
dfs(board, x, y);
return board;
}
void dfs(vector<vector<char>>& board, int i, int j)
{
// 统计该方格地雷的个数
int num = 0;
for(int k = 0; k < 8; k++)
{
int x = i + dx[k];
int y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'M') num++;
}
// 如果有地雷,改完该位置的值后直接退出,该位置不进行dfs了
if(num > 0)
{
board[i][j] = num + '0';
return;
}
else board[i][j] = 'B';
for(int k = 0; k < 8; k++)
{
int x = i + dx[k];
int y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'E')
{
dfs(board, x, y);
}
}
}
};题目七:衣橱整理
家居整理师将待整理衣橱划分为 m x n 的二维矩阵 grid,其中 grid[i][j] 代表一个需要整理的格子。整理师自 grid[0][0] 开始 逐行逐列 地整理每个格子。
整理规则为:在整理过程中,可以选择 向右移动一格 或 向下移动一格,但不能移动到衣柜之外。同时,不需要整理 digit(i) + digit(j) > cnt 的格子,其中 digit(x) 表示数字 x 的各数位之和。
请返回整理师 总共需要整理多少个格子。
示例 1:
输入:m = 4, n = 7, cnt = 5 输出:18
这道题整理过程中,可以向下或向右移动,但是数位之和不能大于cnt,同样是采用dfs即可
与上面的代码类似,同样是创建vis数组,判断该位置是否重复利用
代码如下:
class Solution
{
public:
int dx[2] = {0,1};
int dy[2] = {1,0};
bool vis[101][101];
int ret, m, n, cnt;
int wardrobeFinishing(int _m, int _n, int _cnt)
{
m = _m, n = _n, cnt = _cnt;
dfs(0, 0);
return ret;
}
void dfs(int i, int j)
{
ret++;
vis[i][j] = true;
for(int k = 0; k < 2; k++)
{
int x = i + dx[k];
int y = j + dy[k];
int sum = Count(x, y);
if(x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && sum <= cnt)
{
dfs(x, y);
}
}
}
// 计算(i, j)的数位之和
int Count(int x, int y)
{
int num = 0;
while(x)
{
num += (x % 10);
x /= 10;
}
while(y)
{
num += (y % 10);
y /= 10;
}
return num;
}
};DFS解决floodfill算法的题目到此结束