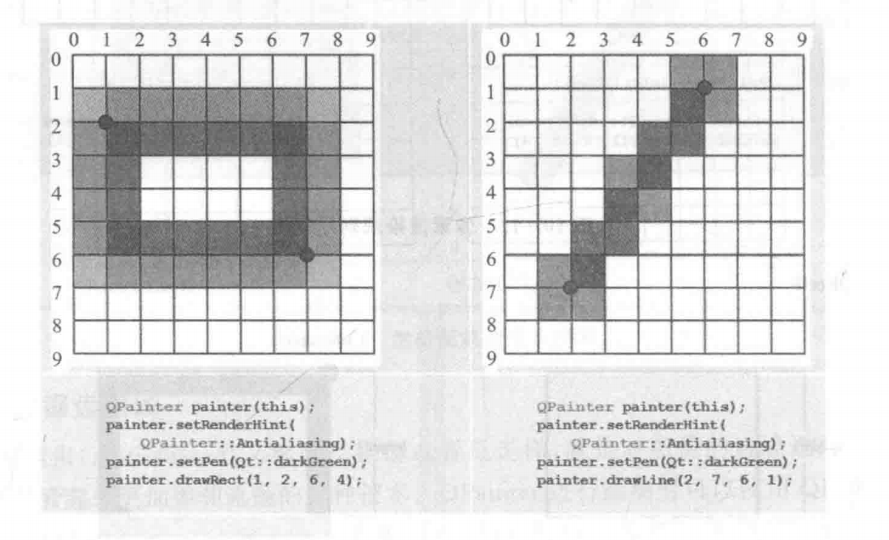
1. 最近刚学回溯和DFS，刷力扣遇到一道题（113题），如下：
   
2. 我们不细究回溯和DFS的区别联系。关于这道题的2种写法，我把第一种称为回溯。

class Solution {
    List<List<Integer>> res = new LinkedList<>();
    LinkedList<Integer> trace = new LinkedList<>();
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        //标准回溯写法
        if (root == null) return res;
        trace.add(root.val);
        targetSum -= root.val;
        backTrack(root, targetSum);
        return res;
    }
    void backTrack (TreeNode root, int targetSum) {
        //标准的回溯写法：1.结束条件2.可选择项:递归调用4.对每一个选择项回溯
        //这种回溯的写法需要先对根节点进行选择。

        //结束条件
        if (0 == targetSum && root.left == null && root.right == null) {
              res.add(new LinkedList<>(trace));
        };
        //可选择项(把节点上的值，看成所在分支)
        if (root.left != null) {
            trace.add(root.left.val);
            targetSum -= root.left.val;
            backTrack(root.left, targetSum); //递归调用
            //回溯
            trace.removeLast();
            targetSum += root.left.val;
        }
        //可选择项(把节点上的值，看成所在分支)
        if (root.right != null) {
            trace.add(root.right.val);
            targetSum -= root.right.val;
            backTrack(root.right, targetSum); //递归调用
            //回溯
            trace.removeLast();
            targetSum += root.right.val;
        }
    }
}

我把第二种方法称为DFS，代码如下：

class Solution {
    List<List<Integer>> res = new LinkedList<>();
    LinkedList<Integer> trace = new LinkedList<>();
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        if (root == null) return res;
        trace.add(root.val);
        targetSum -= root.val;
        if (root.left == null && root.right == null && targetSum == 0) {
            res.add(new LinkedList<>(trace));
        }
        pathSum(root.left, targetSum);
        pathSum(root.right, targetSum);
        trace.removeLast();
        targetSum += root.val;
        return res;
    }
 }

3. 我们知道回溯的标准框架：

backtrack (当前状态) {
	1.判断结束条件
	2.根据当前状态获取下一个状态的选项列表，然后递归
	for (可选项：可选项列表){
		处理可选项;
		backTrack(可选项)；
		撤销可选项；
	}
}

回溯框架的应用场景一般是对分支做选择，而我们这道题的选项都是节点，对于上述的回溯代码，需要把这些节点变成分支，再去套用回溯框架可能更好理解一些。我把节点上的值变到分支上,如图：

接下来，就是套用回溯的框架了，那么我们如何开始调用backtrack()方法呢，具体来说，我们的backtrack方法中传入的root应该是啥呢？值得注意的是，我们的backtrack方法的第一个参数的作用纯粹是为了引出后续的可选分支，我们加入路径的也是后续的可选分支，我们的backtrack方法不对第一个参数(一个分支)做其他事情，通过上图，我们可以看到我们需要通过第一个5这个分支引出4和8这两个分支，而在backtrack这个方法中，5这个分支我们就不会考虑到了，所以我们需要手动去访问5这个分支，并加入路径，也就对应代码：

if (root == null) return res;
trace.add(root.val);
targetSum -= root.val;

有了这一层铺垫之后，后序就可以不断地: 引出可选项–>递归–>回溯了。
4. 我们把第二种方法就叫DFS吧(虽然回溯思想也需要用到DFS算法)。
第二种方法处理的就是节点，我们也可以仿照回溯的代码框架来，但是需要注意不同之处。

• dfs()方法中虽然第一个参数(一个节点)也用于引出后序节点，但是dfs()也会访问这个节点，也就是加入路径，而backtrack第一个参数在调用之前就已经访问过了。
• 可以看到，dfs()是先处理访问节点，再去判断是否结束，而backtrack直接就判断了。
• 因为回溯和dfs对分支和节点的处理时机不同，导致撤销选择时机不同。如下图代码框架：