本人算法萌新,为秋招找工作开始磨炼算法,算法题均用python实现,如果我有哪些地方做的有问题的,还请大家不吝赐教.

1.题干

给你一个由 正整数 组成、大小为 m x n 的矩阵 grid。你可以从矩阵中的任一单元格移动到另一个位于正下方或正右侧的任意单元格（不必相邻）。从值为 c1 的单元格移动到值为 c2 的单元格的得分为 c2 - c1 。

你可以从 任一 单元格开始，并且必须至少移动一次。

返回你能得到的 最大 总得分。

示例 1：

输入：grid = [[9,5,7,3],[8,9,6,1],[6,7,14,3],[2,5,3,1]]

输出：9

解释：从单元格 (0, 1) 开始，并执行以下移动：
- 从单元格 (0, 1) 移动到 (2, 1)，得分为 7 - 5 = 2 。
- 从单元格 (2, 1) 移动到 (2, 2)，得分为 14 - 7 = 7 。
总得分为 2 + 7 = 9 。

示例 2：

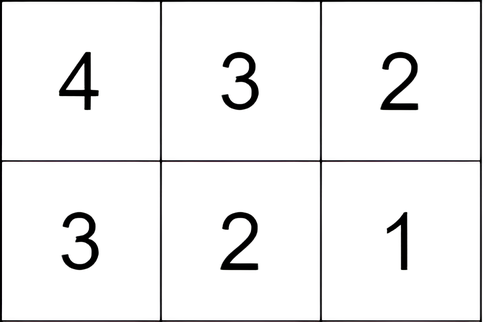
输入：grid = [[4,3,2],[3,2,1]]

输出：-1

解释：从单元格 (0, 0) 开始，执行一次移动：从 (0, 0) 到 (0, 1) 。得分为 3 - 4 = -1 。

提示：

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 1000
• 4 <= m * n <= 105
• 1 <= grid[i][j] <= 105

2.思考

        想了半天,最后只想到复杂度很高的暴力解法.QAQ

3.代码

import math
from typing import List


class Solution:
    def maxScore(self, grid: List[List[int]]) -> int:
        m = len(grid)
        n = len(grid[0])
        dp = [[0 for _ in range(n)] for _ in range(m)]
        mmin = -math.inf
        isb = False
        for i in range(m):
            for j in range(n):
                if i == 0 and j == 0:
                    continue
                if i == 0:
                    x_min = min(grid[i][:j])
                    dp[i][j] = grid[i][j] - x_min
                elif j == 0:
                    y_min = min(row[j] for row in grid[:i])
                    dp[i][j] = grid[i][j] - y_min
                else:
                    x_min = min(grid[i][:j])
                    y_min = min(row[j] for row in grid[:i])
                    dp[i][j] = max(grid[i][j] - x_min, grid[i][j] - y_min)
                if dp[i][j] < 0:
                    mmin = max(mmin, dp[i][j])
                    dp[i][j] = 0
                elif dp[i][j] >= 0:
                    isb = True
                    grid[i][j] -= dp[i][j]
        ans = 0
        for i in range(m):
            for j in range(n):
                if dp[i][j] > ans:
                    ans = dp[i][j]
        if ans == 0 and not isb:
            return mmin
        else:
            return ans


if __name__ == "__main__":
    solution = Solution()
    grid = [[4, 3, 2], [3, 2, 1]]
    print(solution.maxScore(grid))

4.总结

        题解也看得不是很懂,继续加油吧