本文摘要

   本文详细介绍了基于线性二次型调节器（LQR）算法的机器人轨迹跟踪控制方法。首先，文章通过建立基于运动学模型的离散状态方程，来描述机器人的当前状态与目标状态之间的关系，并利用此模型进行状态误差的计算。接着，通过设定状态量和控制量的权重矩阵（Q和R），使用LQR算法求解控制输入u，旨在最小化状态偏差和控制成本，以实现精确的轨迹跟踪。此外，文章还分析了LQR算法在ros_motion_planning运动规划库中的实现，通过源代码详解了误差量化、状态方程动态矩阵的建立、反馈控制增益的计算以及最终控制向量的生成等关键技术步骤。

---

   一、根据运动学模型建立离散的状态方程

   本部分内容已经在之前的文章中详细介绍过了，链接如下：

---

   车辆/单车运动学建模、线性化、离散化过程详细推导【点击可跳转】

---

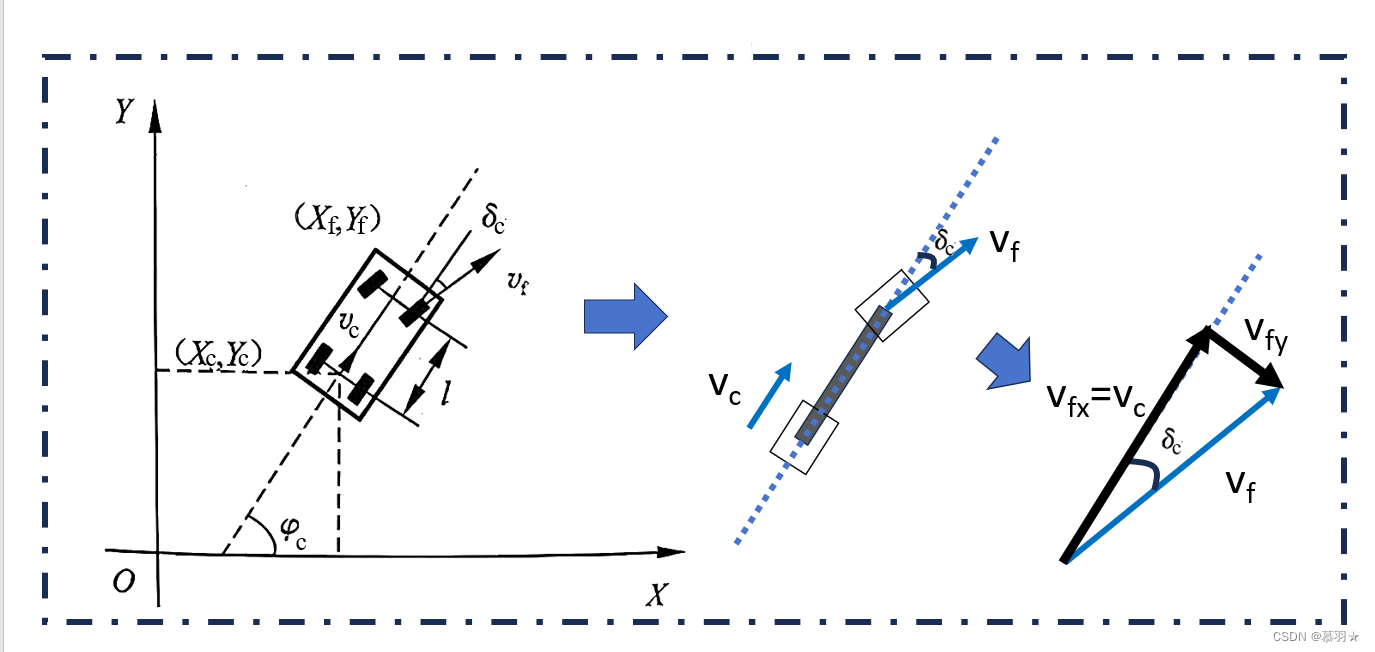
   设机器人当前的位姿为$（x_c,y_c,{\phi }_c）$, 其中$（x_c,y_c,）$ 为其当前位置坐标，${\phi }_c$为其当前姿态角，当前前轮的转向角为${\delta }_c$,当前的后轮车速为$v_c$，前轮车速为$v_f$，前后轮距为$l$，默认采用后轮驱动模式，即可控的是后轮车速$v_c$，如下图所示：

   这里我们直接放一下上文的结论（想了解过程中，可以去看一下上面链接中的文章），将状态量和输入量取为当前量与期望值的差值，即

   $$X=\left[\begin{array}{c}{x}_c-x_r\\ y_c-y_r\\ {\phi }_c-{\phi }_r\end{array}\right],\mathbf{u}=\left[\begin{array}{c}{v}_c-v_r\\ {\delta }_c-{\delta }_r\end{array}\right]$$

   此时：

   $$\begin{array}{rl}\mathbf{X}(\mathrm{k}+1)& =[\begin{array}{ccc}1& 0& -{\mathrm{Tv}}_{\mathrm{r}}\sin {\psi }_{\mathrm{r}}\\ 0& 1& {\mathrm{Tv}}_{\mathrm{r}}\cos {\psi }_{\mathrm{r}}\\ 0& 0& 1\end{array}]\mathbf{X}(\mathrm{k})+\left[\begin{array}{cc}\mathrm{T}\cos {\psi }_{\mathrm{r}}& 0\\ \mathrm{T}\sin {\psi }_{\mathrm{r}}& 0\\ \frac{\mathrm{T}\tan {\delta }_{\mathrm{r}}}{l}& \frac{T{\mathrm{v}}_{\mathrm{r}}}{l{\cos }^2{\delta }_{\mathrm{r}}}\end{array}\right]\mathbf{u}(\mathrm{k})\\ & =\mathrm{AX}(\mathrm{k})+\mathrm{Bu}(\mathrm{k})\end{array}$$

   有了上面的离散化线性运动学模型的状态空间方程，就可以基于此来使用LQR、MPC等控制算法进行轨迹跟踪控制或完成其他控制任务了

---

   二、使用LQR求解控制输入u

   有了第一部分得到的离散的状态空间方程，轨迹跟踪问题就是如何选取合适的输入量u来使得状态量X趋于0，即使得当前状态与期望状态趋于相等（即差值为0），在LQR中目标函数被设定为下式

   $$J=\sum _{k=1}^n(X^{T}QX+u^{T}Ru)$$

   其中，Q为半正定的状态加权矩阵, R为正定的控制加权矩阵，且两者通常取为对角阵；这两个权重矩阵也就是LQR算法需要调节的参数，如果增大Q矩阵中某个元素值，意味着我们期望状态量X中对应的状态能够快速趋近于零，加强跟踪效果，如果增大R矩阵中某个元素值，意味着我们期望输入量u中对应的输入能够快速趋近于零，减少能量损耗。

【补充说明：正定矩阵】给定一个大小为n × n 的实对称矩阵A ，若对于任意长度为n 的非零向量x ，有$x^{T}Ax>0$,则为矩阵A为正定矩阵，有$x^{T}Ax>＝0$,则为矩阵A为半正定矩阵。

   因为，上述LQR目标函数的表达式本质上是一个典型的多目标优化最优控制问题，某一项的权重越大，那么在优化时，减少该项的值，对目标函数值的减少就越明显，自然会优先减少该项的值，从而达到使得该项更快的趋于0。在轨迹跟踪中，前一项优化目标表示跟踪过程路径偏差的累积大小，第二项优化目标表示跟踪过程控制能量的损耗，这样就将轨迹跟踪控制问题转化为一个最优控制问题，两个权重矩阵Q和R就用来平衡这两项的权重。

   对于上述目标函数的优化求解，使用线性二次型调节器 ( Linear-Quadratic Regulator)进行求解，解出的最优控制规律u是关于状态变量X的线性函数，如下所示：

   $$u=-(R+B^{T}PB{)}^{-1}{B}^{T}PAx=Kx$$

   其中，

   $$P=A^{T}PA-A^{T}PB(R+B^{T}PB{)}^{-1}{B}^{T}PA+Q$$

   可以发现解出的u的表达式中仅有P是未知的，P可通过上式进行求解，然而可以发现，上式直接求不好求，所以，我们可以选择求其近似解，

【补充说明：黎卡提方程】
形如${\mathrm{y}}^{\prime }=\mathrm{P}(\mathrm{x}){\mathrm{y}}^2+\mathrm{Q}(\mathrm{x})\mathrm{y}+\mathrm{R}(\mathrm{x})$的非线性微分方程称为黎卡提方程。

   针对黎卡提方程，可以采用循环迭代的思想求解P，具体方法如下：

   ①将等式右边的P初始化为P_old=Q；

   ② 然后用P_old取代等式右边的P来计算等式右边的值，计算结果为P_new

   ③ 比较P_old和P_new，若两者的差值小于预设值， 则认为等式两边相等，我们已经得到了P的近似解，结束循环；否则再令P_old=P_new，继续循环②~③步，直至得到P的近似解或者达到最大迭代次数。

   所以在求解控制输入u时，先通过上面的循环迭代，求出近似的P，然后代入u的表达式，即可得到当前的控制输入u，这里需要注意的是，我们定义的输入u，实际上是当前值与期望值的差值，需要再加上期望值$u_r$才是当前的控制输出指令给机器人执行，进行轨迹跟踪控制。

---

   三、ros_motion_planning运动规划库中实现LQR算法的函数源码解析

   1、源码如下：

/**
 * @brief Execute LQR control process
 * @param s   current state
 * @param s_d desired state
 * @param u_r refered control
 * @return u  control vector
 */
Eigen::Vector2d LQRPlanner::_lqrControl(Eigen::Vector3d s, Eigen::Vector3d s_d, Eigen::Vector2d u_r)
{
  Eigen::Vector2d u;
  Eigen::Vector3d e(s - s_d);
  e[2] = regularizeAngle(e[2]);

  // state equation on error
  Eigen::Matrix3d A = Eigen::Matrix3d::Identity();
  A(0, 2) = -u_r[0] * sin(s_d[2]) * d_t_;
  A(1, 2) = u_r[0] * cos(s_d[2]) * d_t_;

  Eigen::MatrixXd B = Eigen::MatrixXd::Zero(3, 2);
  B(0, 0) = cos(s_d[2]) * d_t_;
  B(1, 0) = sin(s_d[2]) * d_t_;
  B(2, 1) = d_t_;

  // discrete iteration Ricatti equation
  Eigen::Matrix3d P, P_;
  P = Q_;
  for (int i = 0; i < max_iter_; ++i)
  {
    Eigen::Matrix2d temp = R_ + B.transpose() * P * B;
    P_ = Q_ + A.transpose() * P * A - A.transpose() * P * B * temp.inverse() * B.transpose() * P * A;
    if ((P - P_).array().abs().maxCoeff() < eps_iter_)
      break;
    P = P_;
  }

  // feedback
  Eigen::MatrixXd K = -(R_ + B.transpose() * P_ * B).inverse() * B.transpose() * P_ * A;

  u = u_r + K * e;

  return u;
}

   2、主要作用：

   函数_lqrControl执行LQR（线性二次调节器）控制过程，其主要作用是根据当前状态、期望状态和参考控制输入来计算控制向量。这个控制向量旨在最小化路径追踪误差和控制输入的成本，是实现精确路径跟踪的关键。下面将逐段详细介绍这个函数的代码和其功能。

   3、结合第二部分的流程进行详细介绍

Eigen::Vector2d u;
Eigen::Vector3d e(s - s_d);
e[2] = regularizeAngle(e[2]);

   这段代码首先定义控制向量u，然后计算当前状态s和期望状态s_d之间的误差向量e。为了确保角度误差在合理的范围内（-π 到 π），使用regularizeAngle函数处理e[2]，即角度误差部分。

   注：这里的s和s_d分别就是本文第一和第二部分中介绍中当前状态$X_c$和期望状态$X_r$,这里的e就是当前状态与期望状态的差值，也就本文介绍的$X$

// state equation on error
Eigen::Matrix3d A = Eigen::Matrix3d::Identity();
A(0, 2) = -u_r[0] * sin(s_d[2]) * d_t_;
A(1, 2) = u_r[0] * cos(s_d[2]) * d_t_;

Eigen::MatrixXd B = Eigen::MatrixXd::Zero(3, 2);
B(0, 0) = cos(s_d[2]) * d_t_;
B(1, 0) = sin(s_d[2]) * d_t_;
B(2, 1) = d_t_;

   这一部分定义了基于误差的状态方程的动态矩阵A和控制矩阵B。这些矩阵描述了当前状态误差如何随时间演变，以及控制输入如何影响状态误差的演变。A矩阵初始化为单位矩阵，然后通过调整以包含对状态误差动态的描述。B矩阵初始化为零矩阵，然后根据期望状态和控制间隔时间d_t_进行填充。

   注： 这里的A矩阵，跟本文前面给出的A矩阵完全相同，B矩阵的前两行相同，但第三行不同，是因为本文给出的矩阵A和B是按照单车模型进行建模得到的，而该程序是对差速模型进行建模得到的，所以这里不一样

// discrete iteration Ricatti equation
Eigen::Matrix3d P, P_;
P = Q_;
for (int i = 0; i < max_iter_; ++i)
{
  Eigen::Matrix2d temp = R_ + B.transpose() * P * B;
  P_ = Q_ + A.transpose() * P * A - A.transpose() * P * B * temp.inverse() * B.transpose() * P * A;
  if ((P - P_).array().abs().maxCoeff() < eps_iter_)
    break;
  P = P_;
}

   这一段代码通过使用前文介绍的离散迭代黎卡提（Riccati）方程来计算反馈增益矩阵K的中间变量P。P是一个对称正定矩阵，用于评估状态误差的二次成本。这个过程反复迭代，直到P的变化小于设定的阈值eps_iter_或达到最大迭代次数max_iter_。

   注：该过程与前文介绍完全吻合

// feedback
Eigen::MatrixXd K = -(R_ + B.transpose() * P_ * B).inverse() * B.transpose() * P_ * A;

u = u_r + K * e;

   最后，根据计算出的P来，计算反馈增益矩阵K，并使用它来调整参考控制u_r，以最小化误差。这个反馈机制是LQR控制的核心，它确保了即使在存在状态误差的情况下，控制系统也能产生接近最优的控制动作。

   注：该过程与前文介绍完全吻合

   综上所述，_lqrControl函数通过计算基于当前和期望状态的控制动作，实现了对机器人的精确控制，以跟踪给定的路径。这一过程包括误差的量化、系统动态的建模、反馈控制增益的计算，以及最终控制向量的生成。

---

   参考资料：

   1、基础算法 - LQR - 离散时间有限边界

   2、路径规划与轨迹跟踪系列算法学习_第12讲_线性二次型调节器(LQR)法

   3、【自动驾驶】LQR控制实现轨迹跟踪 | python实现 | c++实现

   4、ai-winter/ros_motion_planning

---

---