图像复原算法

news2024/9/21 3:30:06

7.1 逆滤波 (Inverse Filtering)

介绍

逆滤波是一种基本的图像复原方法，用于从退化图像中恢复原始图像。它通过逆向应用退化过程中的滤波器来恢复图像。

原理

逆滤波假设图像在退化过程中受到线性且时不变的滤波器影响，并尝试通过逆向应用该滤波器来恢复原始图像。逆滤波对噪声非常敏感，当噪声较大时，恢复效果可能不理想。

公式

设退化模型为：

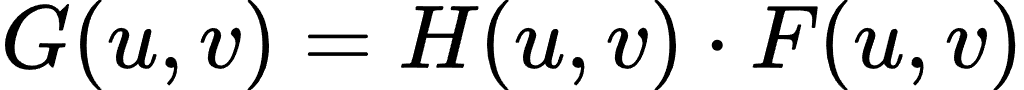
其中，G(u,v) 是退化图像的傅里叶变换，H(u,v) 是退化函数，F(u,v) 是原始图像的傅里叶变换。

逆滤波的复原过程为：

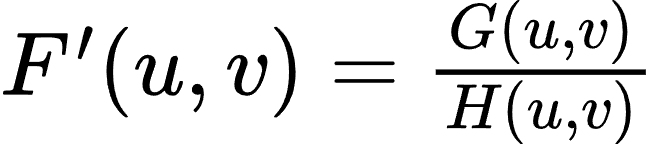
案例

使用Python和OpenCV进行逆滤波图像复原。

代码解析

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像
image = cv2.imread('blurred_image.jpg', 0)

# 进行傅里叶变换
f = np.fft.fft2(image)
fshift = np.fft.fftshift(f)

# 模拟退化函数H(u,v)
rows, cols = image.shape
crow, ccol = rows // 2, cols // 2
H = np.zeros((rows, cols), np.float32)
H[crow - 30:crow + 30, ccol - 30:ccol + 30] = 1

# 应用逆滤波
fshift = fshift / H
f_ishift = np.fft.ifftshift(fshift)
img_back = np.fft.ifft2(f_ishift)
img_back = np.abs(img_back)

# 显示结果
plt.subplot(121), plt.imshow(image, cmap='gray')
plt.title('Blurred Image'), plt.xticks([]), plt.yticks([])

plt.subplot(122), plt.imshow(img_back, cmap='gray')
plt.title('Restored Image'), plt.xticks([]), plt.yticks([])

plt.show()

生活场景案例

逆滤波在去除图像中的简单模糊、恢复轻度失真的图像中有应用，但对噪声非常敏感。

总结

逆滤波是一种基本的图像复原方法，适用于已知退化函数且噪声较小的情况，但在高噪声条件下效果不佳。

7.2 维纳滤波 (Wiener Filtering)

介绍

维纳滤波是一种最优复原方法，通过最小化均方误差来恢复被噪声和退化影响的图像。维纳滤波能够在一定程度上抑制噪声，提升复原效果。

原理

维纳滤波通过平衡噪声与图像的信号，试图在复原过程中减少噪声影响。它结合了逆滤波和噪声抑制的优点，是一种经典的复原算法。

公式

维纳滤波器的表达式为：

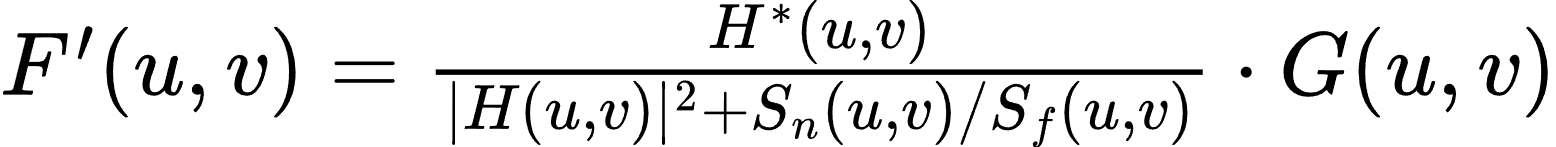
其中，H∗(u,v) 是退化函数的共轭，Sn(u,v)是噪声功率谱，Sf(u,v)是原始图像的功率谱。

案例

使用Python和SciPy进行维纳滤波图像复原。

代码解析

import cv2
import numpy as np
from scipy.signal import wiener
import matplotlib.pyplot as plt

# 读取图像
image = cv2.imread('noisy_blurred_image.jpg', 0)

# 应用维纳滤波
restored_image = wiener(image, (5, 5))

# 显示结果
plt.subplot(121), plt.imshow(image, cmap='gray')
plt.title('Noisy Blurred Image'), plt.xticks([]), plt.yticks([])

plt.subplot(122), plt.imshow(restored_image, cmap='gray')
plt.title('Restored Image'), plt.xticks([]), plt.yticks([])

plt.show()

生活场景案例

维纳滤波在去除噪声和模糊的图像复原中有广泛应用，适用于各种医学图像处理、卫星图像处理等场景。

总结

维纳滤波结合了逆滤波和噪声抑制，适用于含噪声图像的复原，是一种最优的线性复原方法。

7.3 盲复原 (Blind Deconvolution)

介绍

盲复原是一种高级的图像复原方法，不需要先验知识，可以在不完全知道退化函数的情况下恢复图像。它通常通过迭代优化来估计退化函数和原始图像。

原理

盲复原通过反复迭代，交替估计退化函数和原始图像，从而逐步恢复被退化的图像。由于退化函数未知，盲复原的算法复杂度较高，但适应性更强。

公式

盲复原通常通过优化如下目标函数：

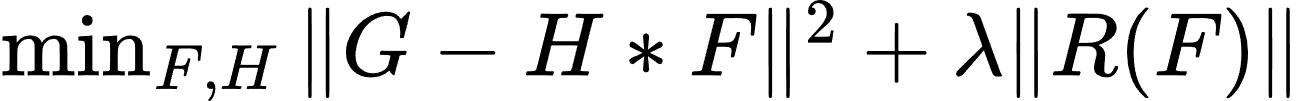
其中，G 是退化图像，F 是估计的原始图像，H 是估计的退化函数，R(F) 是正则化项，λ 是正则化参数。

案例

使用Python和OpenCV进行盲复原。

代码解析

import cv2
import numpy as np
from skimage import restoration
import matplotlib.pyplot as plt

# 读取图像
image = cv2.imread('blurred_image.jpg', 0)

# 模拟退化函数
psf = np.ones((5, 5)) / 25

# 进行盲复原
restored_image, _ = restoration.unsupervised_wiener(image, psf)

# 显示结果
plt.subplot(121), plt.imshow(image, cmap='gray')
plt.title('Blurred Image'), plt.xticks([]), plt.yticks([])

plt.subplot(122), plt.imshow(restored_image, cmap='gray')
plt.title('Restored Image'), plt.xticks([]), plt.yticks([])

plt.show()