---

title: 折半插入排序
date: 2024-7-19 10:17:24 +0800
categories:

• 排序算法
  tags:
• 排序
• 算法
• 折半插入排序
  description: 折半插入排序（Binary Insertion Sort）是插入排序的一种改进版本。它在插入每个元素时使用二分查找（Binary Search）来找到插入位置，从而减少比较次数。
  math: true

---

折半插入排序

折半插入排序（Binary Insertion Sort）是插入排序的一种改进版本。它在插入每个元素时使用二分查找（Binary Search）来找到插入位置，从而减少比较次数。

工作原理

设数组为a[0…n]。

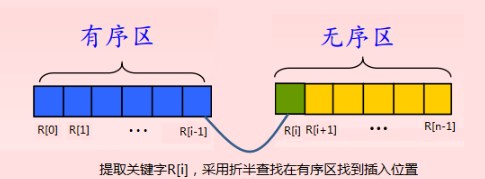
1. 将原序列分成有序区和无序区。a[0…i-1]为有序区，a[i…n] 为无序区。（i从1开始）
2. 从无序区中取出第一个元素，即a[i]，使用二分查找算法在有序区中查找要插入的位置索引j。
3. 将a[j]到a[i-1]的元素后移，并将a[i]赋值给a[j]。
4. 重复步骤2~3，直到无序区元素为0。

示例

假设有一个待排序的列表：[12, 11, 13, 5, 6]

第一步

• 第一个元素 12 已经排序。

第二步

• 取出 11，使用二分查找找到插入位置（在 12 之前）。
• 移动元素，将 11 插入到正确位置。
  [11, 12, 13, 5, 6]

第三步

• 取出 13，使用二分查找找到插入位置（在 12 之后）。
• 不需要移动元素，直接插入 13。

[11, 12, 13, 5, 6]

第四步

• 取出 5，使用二分查找找到插入位置（在 11 之前）。
• 移动元素，将 5 插入到正确位置。

[5, 11, 12, 13, 6]

第五步

• 取出 6，使用二分查找找到插入位置（在 5 之后）。
• 移动元素，将 6 插入到正确位置。

[5, 6, 11, 12, 13]

复杂度分析

折半插入排序通过减少比较次数来提高效率，但在元素移动次数上与普通插入排序一致。

时间复杂度

• 最坏情况时间复杂度：$O(n^2)$ （主要由于元素移动次数）
• 平均情况时间复杂度：$O(n^2)$
• 最好情况时间复杂度：$O(n\log n)$（比较次数）

空间复杂度

• 空间复杂度：$O(1)$

代码实现

以下是折半插入排序的Java实现代码：

public class BinaryInsertionSort {
    public static void binaryInsertionSort(int[] arr) {
        int n = arr.length;
        
        // 从数组的第二个元素开始遍历
        for (int i = 1; i < n; i++) {
            int key = arr[i]; // 需要插入的元素
            int left = 0; // 二分查找的左边界
            int right = i; // 二分查找的右边界

            // 使用二分查找找到插入位置
            while (left < right) {
                int mid = (left + right) / 2;
                if (arr[mid] <= key) {
                    left = mid + 1; // 在右半部分查找
                } else {
                    right = mid; // 在左半部分查找
                }
            }

            // 将大于key的元素向后移动一位
            for (int j = i; j > left; j--) {
                arr[j] = arr[j - 1];
            }
            arr[left] = key; // 将key插入到正确的位置
        }
    }

    public static void main(String[] args) {
        int[] arr = {12, 11, 13, 5, 6};
        binaryInsertionSort(arr);
        for (int i : arr) {
            System.out.print(i + " ");
        }
    }
}