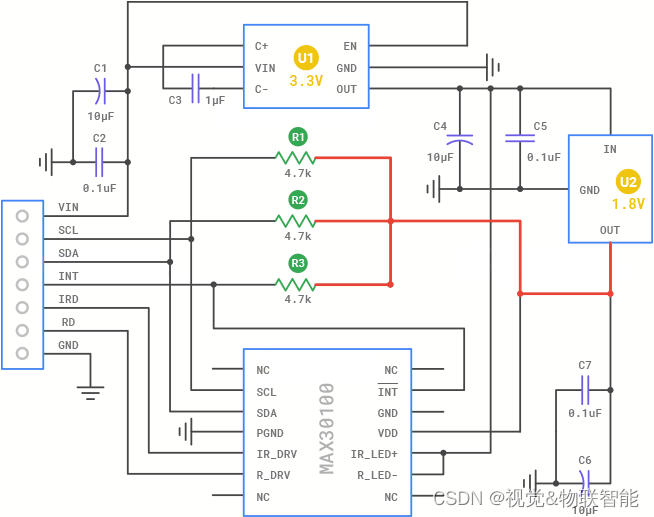
1 梯度下降法

本文所有的数学定义概念非官方所给，皆来自于个人理解融合

1.1 梯度的定义

个人理解就是能够使函数值增大最快的方向
需要明确的一点，这里说的方向都是自变量变化的方向

1.2 梯度下降法

梯度下降法本质上是用来求解目标函数最小值的一种数学方法。

拿最简单的f(x)=x²举例

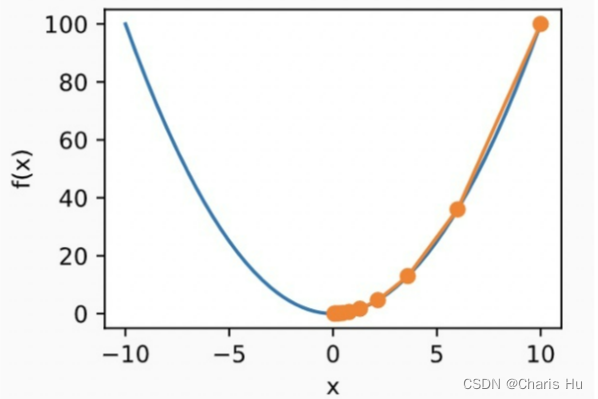
假如我们的起始点是（10，100），我们的目的是求f(x)的最小值，这时可利用梯度下降法求解。

对f(x)求导后，f(x)的导数为2x，在起始点的梯度为20，这里20可理解为一个向量，也就是既有方向，也有大小。

此外，f(x)=x²自变量只有一个x，也就是说自变量的变化方向要么是x的正方向，要么是x的负方向，我们求得x=10的梯度为20，根据梯度的定义，这就表示x沿着梯度20这个方向变化，函数值能最快增长。

当然这个在单个自变量看起来不是很直观，只能看出函数值沿着正负反向是否增长，无法反映出快慢。

我们就简单理解成沿着20这个方向增长（的最快）。另外，此处的20根据上面提到实际上是个向量，这个向量尾其实是原点这个点，实际梯度方向就是x轴正方向，长度为20的一个向量。

为了能取到函数的最小值，我们自然应该取梯度的反方向，也就是沿着x轴的负方向走才能得到函数最小值，于是每次x迭代应该按照下面这个公式进行迭代

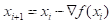
当然，这还会出现一些问题，因为我们刚才提到梯度是有方向、有大小的向量，方向这个是决定函数值增长最快的方向，这个没有疑问。那大小呢？可以想到，如果我们不调整大小，大概会出现一些问题，比如可能会在两个x之间反复横跳，因为每次梯度更新，它们的f(x)值是相同的，比如从起始点（10，100）迭代后为（-10，100），不断循环，具体可以看这个视频理解一下。

所以我们引入了一个步长的概念，在机器学习中称之为学习率

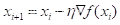
通过调整$n$的大小，我们就可以调整每次梯度下降的一个幅度，避免出现上述视频中的问题，这个学习率设置很玄学，如果我们把它搞得比1大，那有可能f(x)就会在x迭代过程中不断增长，那就违背了我们的初衷，所以一般设置的比1小，但具体小多少，要根据实际情况，经验值好像在0.01-0.05之间，当然这个要根据f(x)的实际情况，好像和梯度大小也有一定的关系。如果我们设置的太小，有可能导致迭代时间过长，迭代几百上千次还没有到最小值，也有可能我们设置的偏大，导致在迭代过程中错过了最小值点，所以还是有一定玄学。

以上是关于梯度下降法的理解。

当然我们也可以把梯度下降法迁移到两个自变量的表达式中更为直观，如f(x,y)这种，类似于下面这种图形。

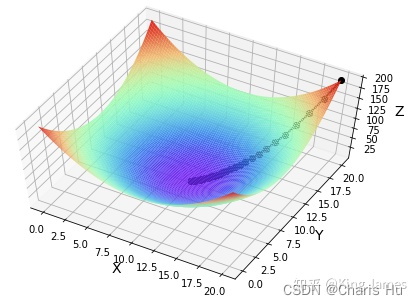
这里自变量是x和y，那么变化的方向就是由x和y组成的向量，如我们求一个二元函数的梯度为（10，20），那么能使得这个函数值增长最快的变化方向就是（10，20），这个向量也是相对于原点来说的。从图上就可以直观理解到什么叫上升最快了。