深度学习——神经网络(neural network)详解(二). 手算步骤,步骤清晰0基础可看
前文如下:深度学习——神经网络(neural network)详解(一). 带手算步骤,步骤清晰0基础可看
运用神经网络模型进行房价预测具体手算过程,具体示例
假设我们有一个简单的神经网络,还是之前这个神经网络,输入层2个节点,隐藏层3个节点,输出层1个节点。我们使用以下简化的示例数据:
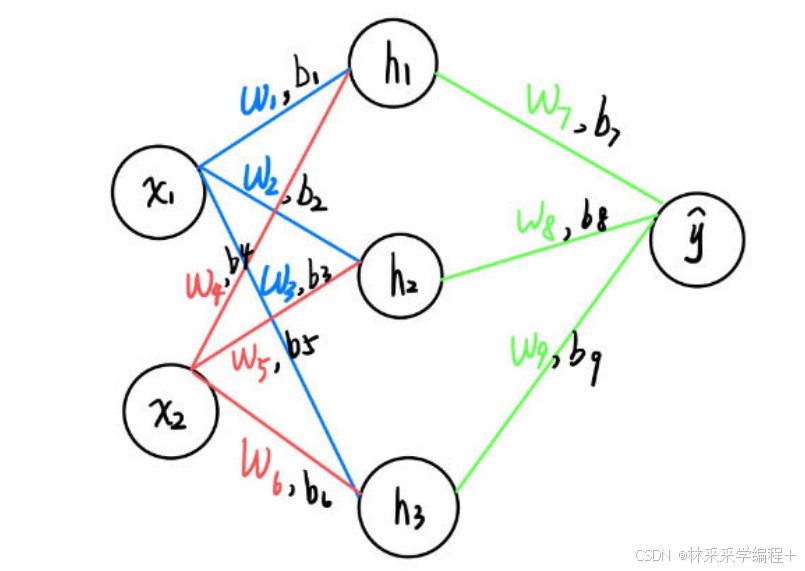
(一)函数介绍
-
Sigmoid 函数:我们把Sigmoid 函数作为激活函数,用于数组的映射转换,公式为:
σ ( z ) = 1 1 + e − z \sigma(z) = \frac{1}{1 + e^{-z}} σ(z)=1+e−z1 -
Sigmoid 函数的导数:反向传播中计算梯度所需的导数,公式为:
σ ′ ( z ) = σ ( z ) ( 1 − σ ( z ) ) \sigma'(z) = \sigma(z)(1 - \sigma(z)) σ′(z)=σ(z)(1−σ(z)) -
均方误差(MSE)损失函数:衡量预测值与实际值差异的指标,公式为:
L = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 L = \frac{1}{n} \sum_{i=1}^{n}(y_i - \hat{y}_i)^2 L=n1i=1∑n(yi−y^i)2
在单样本情况下简化为:
L = ( y − y ^ ) 2 L = (y - \hat{y})^2 L=(y−y^)2 -
均方误差(MSE)损失函数的导数:
在单样本情况下简化为:
∂ L ∂ y ^ = − 2 ( y − y ^ ) \frac{\partial L}{\partial \hat{y}} = -2(y-\hat{y}) ∂y^∂L=−2(y−y^)
4.权重的梯度
涉及到
w
1
w_{1}
w1的公式如下:
L
=
(
y
−
y
^
)
2
L = (y - \hat{y})^2
L=(y−y^)2
y
^
=
σ
(
w
7
h
1
+
w
8
h
2
+
w
9
h
3
)
\hat{y} = \sigma(w_7 h_1 + w_8 h_2 + w_9 h_3)
y^=σ(w7h1+w8h2+w9h3)
h
1
=
σ
(
w
1
x
1
+
b
1
+
w
4
x
2
+
b
4
)
h_1 = \sigma(w_{1}x_1 + b_1+ w_{4}x_2 + b_4)
h1=σ(w1x1+b1+w4x2+b4)
比如对于
w
1
w_{1}
w1,其求梯度公式为:
d
L
d
w
1
=
d
L
d
y
^
⋅
d
y
^
d
h
1
⋅
d
h
1
d
w
1
\frac{dL}{dw_{1}} = \frac{dL}{d\hat{y}} \cdot \frac{d\hat{y}}{dh_{1}} \cdot \frac{dh_{1}}{dw_{1}}
dw1dL=dy^dL⋅dh1dy^⋅dw1dh1
(1)
d
L
d
y
^
=
−
2
(
y
−
y
^
)
\frac{dL}{d\hat{y}}=-2(y-\hat{y})
dy^dL=−2(y−y^)
(2)计算
d
y
^
d
h
1
\frac{d\hat{y}}{dh_{1}}
dh1dy^
令
z
=
w
7
h
1
+
w
8
h
2
+
w
9
h
3
z=w_7 h_1 + w_8 h_2 + w_9 h_3
z=w7h1+w8h2+w9h3,
则
y
^
=
σ
(
z
)
=
σ
(
w
7
h
1
+
w
8
h
2
+
w
9
h
3
)
\hat{y}=\sigma(z)=\sigma(w_7 h_1 + w_8 h_2 + w_9 h_3)
y^=σ(z)=σ(w7h1+w8h2+w9h3),
而
σ
′
(
z
)
=
σ
(
z
)
(
1
−
σ
(
z
)
)
\sigma'(z) = \sigma(z)(1 - \sigma(z))
σ′(z)=σ(z)(1−σ(z))
所以
d
y
^
d
h
1
=
σ
(
z
)
⋅
(
1
−
σ
(
z
)
)
⋅
d
z
d
h
1
\frac{d\hat{y}}{dh_{1}}=\sigma(z)\cdot(1 - \sigma(z))\cdot\frac{dz}{dh_{1}}
dh1dy^=σ(z)⋅(1−σ(z))⋅dh1dz
d
y
^
d
h
1
=
(
w
7
h
1
+
w
8
h
2
+
w
9
h
3
)
⋅
(
1
−
(
w
7
h
1
+
w
8
h
2
+
w
9
h
3
)
)
⋅
w
7
\frac{d\hat{y}}{dh_{1}}=(w_7 h_1 + w_8 h_2 + w_9 h_3)\cdot(1 - (w_7 h_1 + w_8 h_2 + w_9 h_3))\cdot w_7
dh1dy^=(w7h1+w8h2+w9h3)⋅(1−(w7h1+w8h2+w9h3))⋅w7
(3)同理计算
d
h
1
d
w
1
\frac{dh_{1}}{dw_{1}}
dw1dh1
h
1
=
σ
(
w
1
x
1
+
b
1
+
w
4
x
2
+
b
4
)
h_1 = \sigma(w_{1}x_1 + b_1+ w_{4}x_2 + b_4)
h1=σ(w1x1+b1+w4x2+b4)
d
h
1
d
w
1
=
(
w
1
x
1
+
b
1
+
w
4
x
2
+
b
4
)
⋅
(
1
−
(
w
1
x
1
+
b
1
+
w
4
x
2
+
b
4
)
)
⋅
x
1
\frac{dh_{1}}{dw_{1}}=(w_{1}x_1 + b_1+ w_{4}x_2 + b_4)\cdot(1 - (w_{1}x_1 + b_1+ w_{4}x_2 + b_4))\cdot x_1
dw1dh1=(w1x1+b1+w4x2+b4)⋅(1−(w1x1+b1+w4x2+b4))⋅x1
所以
d
L
d
w
1
=
d
L
d
y
^
⋅
d
y
^
d
h
1
⋅
d
h
1
d
w
1
=
−
2
(
y
−
y
^
)
⋅
(
w
7
h
1
+
w
8
h
2
+
w
9
h
3
)
(
1
−
(
w
7
h
1
+
w
8
h
2
+
w
9
h
3
)
)
w
7
⋅
(
w
1
x
1
+
b
1
+
w
4
x
2
+
b
4
)
(
1
−
(
w
1
x
1
+
b
1
+
w
4
x
2
+
b
4
)
)
x
1
\frac{dL}{dw_{1}} = \frac{dL}{d\hat{y}} \cdot \frac{d\hat{y}}{dh_{1}} \cdot \frac{dh_{1}}{dw_{1}}=-2(y-\hat{y}) \cdot (w_7 h_1 + w_8 h_2 + w_9 h_3) (1 - (w_7 h_1 + w_8 h_2 + w_9 h_3)) w_7 \cdot (w_{1}x_1 + b_1+ w_{4}x_2 + b_4) (1 - (w_{1}x_1 + b_1+ w_{4}x_2 + b_4)) x_1
dw1dL=dy^dL⋅dh1dy^⋅dw1dh1=−2(y−y^)⋅(w7h1+w8h2+w9h3)(1−(w7h1+w8h2+w9h3))w7⋅(w1x1+b1+w4x2+b4)(1−(w1x1+b1+w4x2+b4))x1
(二)参数更新过程
1.输入数据(样本)
- 输入特征: X = [ 120 , 1 ] X = [120, 1] X=[120,1](面积120平方米,市中心位置)
- 目标值: y = 300 , 000 y = 300,000 y=300,000(房价300,000元)
2.输入到隐藏层的权重和偏置随机初始化
- 权重 W h = [ w 1 , w 2 , w 3 , w 4 , w 5 , w 6 ] = [ 0.2 , 0.3 , 0.4 , 0.5 , 0.6 , 0.7 ] W_h = [w_1, w_2, w_3, w_4, w_5, w_6] = [0.2, 0.3, 0.4, 0.5, 0.6, 0.7] Wh=[w1,w2,w3,w4,w5,w6]=[0.2,0.3,0.4,0.5,0.6,0.7]
- 偏置 b h = [ b 1 , b 2 , b 3 , b 4 , b 5 , b 6 , b 7 , b 8 , b 9 ] = [ 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 ] b_h = [b_1, b_2, b_3,b_4, b_5, b_6,b_7, b_8, b_9] = [0, 0, 0,0, 0, 0,0, 0, 0] bh=[b1,b2,b3,b4,b5,b6,b7,b8,b9]=[0,0,0,0,0,0,0,0,0](假设偏置为0)
3.激活函数输出
h
1
=
σ
(
w
1
⋅
x
1
+
w
4
⋅
x
2
)
h_1 = \sigma(w_1 \cdot x_1 + w_4 \cdot x_2)
h1=σ(w1⋅x1+w4⋅x2)
h
2
=
σ
(
w
2
⋅
x
1
+
w
5
⋅
x
2
)
h_2 = \sigma(w_2 \cdot x_1 + w_5 \cdot x_2)
h2=σ(w2⋅x1+w5⋅x2)
h
3
=
σ
(
w
3
⋅
x
1
+
w
6
⋅
x
2
)
h_3 = \sigma(w_3 \cdot x_1 + w_6 \cdot x_2)
h3=σ(w3⋅x1+w6⋅x2)
4.具体计算
h
1
=
σ
(
0.2
×
120
+
0.5
×
1
)
=
σ
(
24.2
)
h_1 = \sigma(0.2 \times 120 + 0.5 \times 1)=\sigma(24.2)
h1=σ(0.2×120+0.5×1)=σ(24.2)
h
2
=
σ
(
0.3
×
120
+
0.6
×
1
)
=
σ
(
37.8
)
h_2 = \sigma(0.3 \times 120 + 0.6 \times 1)=\sigma(37.8)
h2=σ(0.3×120+0.6×1)=σ(37.8)
h
3
=
σ
(
0.4
×
120
−
0.7
×
1
)
=
σ
(
46.3
)
h_3 = \sigma(0.4 \times 120 - 0.7 \times 1)=\sigma(46.3)
h3=σ(0.4×120−0.7×1)=σ(46.3)
假设 σ ( 24.2 ) ≈ 0.99 \sigma(24.2) \approx 0.99 σ(24.2)≈0.99, σ ( 37.8 ) ≈ 0.998 \sigma(37.8) \approx 0.998 σ(37.8)≈0.998, σ ( 46.3 ) ≈ 0.999 \sigma(46.3) \approx 0.999 σ(46.3)≈0.999(这里取Sigmoid函数的近似值)
5.隐藏到输出层的权重
- 权重 W o = [ w 7 , w 8 , w 9 ] = [ 0.1 , 0.2 , 0.3 ] W_o = [w_7, w_8, w_9] = [0.1, 0.2, 0.3] Wo=[w7,w8,w9]=[0.1,0.2,0.3]
6.输出层预测值
y ^ = σ ( w 7 ⋅ h 1 + w 8 ⋅ h 2 + w 9 ⋅ h 3 ) ≈ 0.6452 \hat{y} = \sigma(w_7 \cdot h_1 + w_8 \cdot h_2 + w_9 \cdot h_3)\approx 0.6452 y^=σ(w7⋅h1+w8⋅h2+w9⋅h3)≈0.6452
7.损失计算
L = ( 300 , 000 − y ^ ) 2 ≈ ( 300 , 000 − 0.6452 ) 2 ≈ 89 , 999 , 810 , 000 L = (300,000 - \hat{y})^2 \approx (300,000 - 0.6452 )^2 \approx 89,999,810,000 L=(300,000−y^)2≈(300,000−0.6452)2≈89,999,810,000(这里取 y ^ \hat{y} y^ 的近似值进行计算,这个损失也太大了)
8.梯度计算
(1) d L d y ^ = − 2 ( y − y ^ ) = − 2 ( 300 , 000 − 0.6452 ) ≈ − 599 , 998.7096 \frac{dL}{d\hat{y}}=-2(y-\hat{y})=−2(300,000−0.6452)\approx −599,998.7096 dy^dL=−2(y−y^)=−2(300,000−0.6452)≈−599,998.7096
(2) d y ^ d h 1 / d h 2 / d h 3 \frac{d\hat{y}}{dh_{1}/dh_{2}/dh_{3}} dh1/dh2/dh3dy^
d y ^ d h 1 = ( w 7 h 1 + w 8 h 2 + w 9 h 3 ) ⋅ ( 1 − ( w 7 h 1 + w 8 h 2 + w 9 h 3 ) ) ⋅ w 7 ) ≈ 0.024 \frac{d\hat{y}}{dh_{1}}=(w_7 h_1 + w_8 h_2 + w_9 h_3)\cdot(1 - (w_7 h_1 + w_8 h_2 + w_9 h_3))\cdot w_7)\approx0.024 dh1dy^=(w7h1+w8h2+w9h3)⋅(1−(w7h1+w8h2+w9h3))⋅w7)≈0.024
d y ^ d h 2 = ( w 7 h 1 + w 8 h 2 + w 9 h 3 ) ⋅ ( 1 − ( w 7 h 1 + w 8 h 2 + w 9 h 3 ) ) ⋅ w 8 ) ≈ 0.048 \frac{d\hat{y}}{dh_{2}}=(w_7 h_1 + w_8 h_2 + w_9 h_3)\cdot(1 - (w_7 h_1 + w_8 h_2 + w_9 h_3))\cdot w_8)\approx0.048 dh2dy^=(w7h1+w8h2+w9h3)⋅(1−(w7h1+w8h2+w9h3))⋅w8)≈0.048
d y ^ d h 3 = ( w 7 h 1 + w 8 h 2 + w 9 h 3 ) ⋅ ( 1 − ( w 7 h 1 + w 8 h 2 + w 9 h 3 ) ) ⋅ w 9 ) ≈ 0.07 \frac{d\hat{y}}{dh_{3}}=(w_7 h_1 + w_8 h_2 + w_9 h_3)\cdot(1 - (w_7 h_1 + w_8 h_2 + w_9 h_3))\cdot w_9)\approx0.07 dh3dy^=(w7h1+w8h2+w9h3)⋅(1−(w7h1+w8h2+w9h3))⋅w9)≈0.07
(3)
d
h
1
d
w
1
\frac{dh_{1}}{dw_{1}}
dw1dh1
d
h
1
d
w
1
=
(
w
1
x
1
+
b
1
+
w
4
x
2
+
b
4
)
⋅
(
1
−
(
w
1
x
1
+
b
1
+
w
4
x
2
+
b
4
)
)
⋅
x
1
=
−
69090
\frac{dh_{1}}{dw_{1}}=(w_{1}x_1 + b_1+ w_{4}x_2 + b_4)\cdot(1 - (w_{1}x_1 + b_1+ w_{4}x_2 + b_4))\cdot x_1=−69090
dw1dh1=(w1x1+b1+w4x2+b4)⋅(1−(w1x1+b1+w4x2+b4))⋅x1=−69090
d L d w 1 = d L d y ^ ⋅ d y ^ d h 1 ⋅ d h 1 d w 1 = − 599 , 998.7096 × 0.024 × ( − 69090 ) = 994893860 \frac{dL}{dw_{1}} = \frac{dL}{d\hat{y}} \cdot \frac{d\hat{y}}{dh_{1}} \cdot \frac{dh_{1}}{dw_{1}}=−599,998.7096\times 0.024\times(−69090)=994893860 dw1dL=dy^dL⋅dh1dy^⋅dw1dh1=−599,998.7096×0.024×(−69090)=994893860
8.梯度更新
这里我们将学习率
α
\alpha
α设置为0.001。
w
1
n
e
w
=
α
⋅
∂
L
∂
w
1
o
l
d
=
0.001
×
994893860
=
94893.86
w_{1} ^{new}= \alpha \cdot \frac{\partial L}{\partial w_{1}^{old}} =0.001\times994893860 =94893.86
w1new=α⋅∂w1old∂L=0.001×994893860=94893.86
到此为止,我们利用一个样本 [ x 1 , x 2 ] = [ 120 , 1 ] [{x_{1},x_{2}}]=[{120,1}] [x1,x2]=[120,1]和这个简单的神经网络对参数 w 1 w_{1} w1的更新已经完成。
后续步骤就是按照更新 w 1 w_{1} w1的方法对其他参数进行更新,当所有参数都更新完一次后,被称作一次迭代(iteration)。当你拥有的数据集中的所有数据都输入模型被训练一次,被称作一轮(epoch)。我们的模型训练好需要多个轮次,几百轮或者上千轮。
一个简单的神经网络的迭代过程演示到这里就结束了。