C++分析哈希表

哈希表

哈希表介绍

哈希表的数据插入和查找原理

哈希表的存放方法

开散列解决哈希冲突

思路

代码设计

结构设计

数据插入

数据查找

数据删除

闭散列解决哈希冲突

思路

代码设计

结构设计

数据插入

数据查找

数据删除

析构函数设计

比较key相等以及key转int仿函数

哈希表

哈希表介绍

前面学习到的数据结构中，每一个数据与其位置没有相对映射关系，所以在比较时必须每一个元素都参与比较，顺序结构下的时间复杂度为O(N)，平衡二叉搜索树下的时间复杂度为O( $log_{2}{N}$ )，为了使效率最优化，考虑使用一个新的数据结构：哈希表/散列表，该数据结构可以在查找中根据存储位置快速定位需要查找的元素，理论上的时间复杂度为O(1)

哈希表的数据插入和查找原理

数据插入：插入时会将数据通过哈希函数计算出在哈希表中的相对位置再存入

数据查找：查找时通过哈希函数计算查找的值可能出现的相对位置，从该位置读取是否存在需要查找的值

上面两种对数据处理的方法就成为哈希方法，使用到哈希函数计算相对位置，数据存储的位置即为哈希表/散列表结构

一般情况下来说，哈希函数可以设置为如下：

$hash(key) = key \bmod capacity$

其中， $key$ 为原始数据， $capacity$ 为实际数据容量，例如在 $capacity$ 为10的一个数组中，插入以下数据：

int data[] = {1,7,6,4,5,9};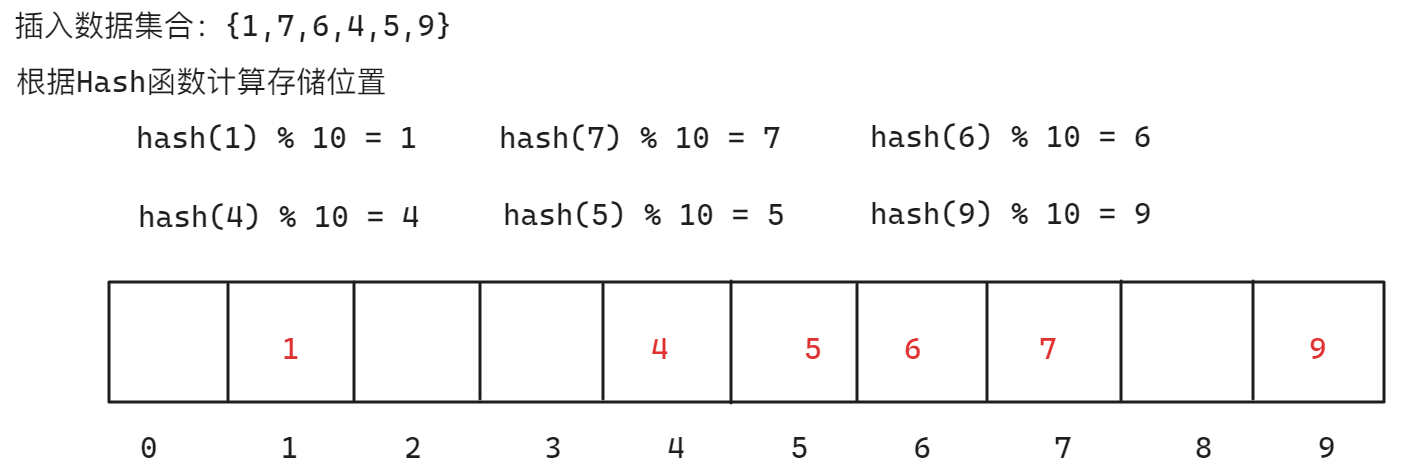

当查找时，如果查找的key值为7，则根据哈希函数计算存储位置为7，在下标为7的位置比对关键值，相等则查找完毕

哈希表的存放方法

直接定址法：直接定址就是直接确定地址，用 $key$ 的值映射到一个绝对位置或者相对位置
除留余数法：通过 $hash(key) = key \bmod capacity$ 函数计算出存储位置

对于直接定址法来说，因为key的值基本上就是对应的位置，所以根据key可以直接找到相对位置，时间复杂度基本上为O(1)，并且每一个key只有对应的一个位置，不存在冲突情况，但是这种方法的缺点就是依赖key的集中程度，如果key值集中程度高，那么所开辟的空间也就相对较小，如果key值集中程度低，那么可能会造成开辟的空间很大，但是实际使用的部分却很少

对于除留余数法来说，因为通过哈希函数 $hash(key) = key \bmod capacity$ 计算存储位置，所以其存储位置不会超过表的大小，但是存在通过哈希函数计算得到的余数相同的情况，所以会有冲突的情况，常见的解决冲突方法有两种：

开散列：开放定址法，常见的有：线性探测、二次探测
闭散列：哈希桶/拉链法

开散列解决哈希冲突

思路

使用开放定址法中的线性探测方法为例

线性探测：根据哈希函数$hash(key) = key % capacity$计算出相对位置，如果该位置已经有值，则向后移动一个单位长度，如果后一个位置也存在值，则继续向后移动一个单位，以此类推

例如插入在 $capacity=10$ 时插入下面的数据：

int data[] = {1,7,6,4,5,9,15,16,11,21};

此时如果再想插入新的数据就会因为找不到空位置而插入失败，为了防止在插入过程中出现的容量不足的问题，解决哈希冲突的过程中也会引入负载因子/载荷因子，负载因子/载荷因子α=已经存储的元素个数/哈希表结构的容量，如果负载因子的值超过指定的数值，那么就需要进行扩容，对于开放定址法来说，一般负载因子在0.7-0.8以下

代码设计

结构设计

每一个插入的数据结构设计，以键值对为例，还需要处理在查找/删除时需要用到的哈希表位置状态，在开散列中，位置一共有三种状态

// 哈希表每个数据结构
template<class K, class V>
struct HashData
{
    pair<K, V> _kv;
    Status _st;// 位置状态
};

哈希表结构设计，需要一个vector类型数组充当表结构，为了计算负载因子，需要引入变量_count统计插入的数据个数

Empty状态
Delete状态
Exist状态

// 哈希表结构
template<class K, class V>
class hashtable
{
public:
    hashtable()
        : _table(10, Empty)
        , _count(0)
    {}

private:
    vector<HashData> _table;// 哈希表
    size_t _count;// 数据个数
};

数据插入

处理数据插入：根据除留余数法，需要通过哈希函数$hash(key) = key % capacity$计算出存储位置，再找到空位置（不是删除位置和存在位置），当负载因子到达一定程度（本次设计为0.7）时进行扩容

设计时需要考虑到下面的问题：

哈希函数中的 $capacity$ 是容量，但是对于vector来说不是capacity()，而是size()，因为size()才是实际可以存储的容量，capacity()是备用的容量，多出来的部分不可以存储数值，并且[]无法访问size()外的数据
计算负载因子时，需要注意_count和size()的值都是整型，所以进行除法时，计算的结果不可能出现小数部分，可以将_count和size()中的其中一个转化为小数类型，或者将_count乘以10，负载因子也乘以10，此时计算的结果依旧为整数，本次采用第二种方法
扩容时，可以考虑重新创建一个vector类型的新数组newTable，其大小是已经存在的表的大小的2倍，但是需要注意，扩容过后，部分值通过哈希函数计算出来的位置可能发生改变，例如当 $capacity$ 为10时，11的存储位置为1，但是 $capacity$ 为20时，11的存储位置为11，此时还需要进行重新插入，所以为了减少插入逻辑的重复，可以考虑创建一个新的hash表对象，该对象中的_table成员大小是原来对象的2倍，新对象调用insert函数重新插入即可，插入时需要确保数据是未删除以及不为空的数据
本次实现的是不重复的键值对，所以如果出现重复的键值对时不能成功插入（调用接下来需要实现的find()函数）
因为负载因子到达0.7的时候就会进行扩容，所以在遍历过程中理论上不会存在所有位置都是Exist状态，所以遍历空位置时可以使用判断Exist状态作为循环条件

    // 存在时不插入
    if (find(kv))
    {
        return false;
    }
    
    // 扩容
    if (_count * 10 / _table.size() >= 7)
    {
        // 创建新表改变大小
        hashtable ht(_table.size() * 2);
        // 遍历原表依次插入到新表
        size_t i = 0;
        while (i < _table.size())
        {
            if (_table[i]._st == Exist)
            {
                ht.insert(_table[i++]);
            }
        }

        _table.swap(ht._table);
    }

    // 计算存储位置
    size_t hashi = kv.first % _table.size();
    // 找到存储位置(删除/空)
    while (_table[hashi]._st != Exist)
    {
        ++hashi;
        // 如果空位置在前面，并且起始位置之后再没有空位置时需要回到下标为0的位置
        hashi %= _table.size();
    }

    // 找到空位置时插入
    _table[hashi]._kv = kv;
    _table[hashi]._st = Exist;
    // 计数
    ++_count;

    return true;
}

数据查找

哈希表中的数据查找返回对应值位置的地址，根据key找到对应位置，如果该位置是Exist状态，比较key是否匹配，如果不匹配继续向后匹配位置是Exist状态时的key，查找时需要注意只有是存在状态的值才可以查找

HashData<K, V>* find(const K& key)
{
    // 找到存储位置
    size_t hashi = key % _table.size();
    while (_table[hashi]._st == Exist)
    {
        if (_table[hashi]._kv.first == key)
        {
            return &_table[hashi];
        }
        ++hashi;
        hashi %= _table.size();
    }

    return nullptr;
}

数据删除

数据删除的思路：调用find函数，如果找到则将位置状态修改为Delete，改变数据个数_count，删除成功返回true，否则返回false

// 数据删除
bool erase(const K& key)
{
    HashData<K, V>* ret = find(key);
    if (ret)
    {
        ret->_st = Empty;
        return true;
    }

    return false;
}

闭散列解决哈希冲突

前面的开散列最大的问题就是会彼此占用空间，需要多一项规则计算位置，不论是二次探测还是线性探测都是一样的原理，为了解决这种问题，采用闭散列

思路

使用哈希桶/拉链法为例

哈希桶/拉链法原理：开辟一个指针数组，每一个指针指向存储的键值对

以插入下面的元素为例：

int data[] = {1,7,6,4,5,9,15,16,11,21};

在哈希桶中也存在负载因子/载荷因子，但是哈希桶中的负载因子α一般在1左右

代码设计

结构设计

对于每一个哈希表数据就是一个链表节点，所以按照链表节点的形式定义即可

// 哈希数据节点
template <class K, class V>
struct HashData
{
    pair<K, V> _kv;
    HashData<K, V>* _next;
};

哈希表结构设计中需要注意是指向哈希数据节点的指针数组

// 哈希表结构
template <class K, class V>
class hashtable
{
    typedef HashData<K, V> Node;
private:
    vector<Node*> _table;
    size_t _count;
};

数据插入

处理数据插入即为链表的插入，这里有两种插入方式，一种是头插，另一种是尾插，但是因为尾插需要找尾，所以使用头插

不使用list是因为便于处理后面封装的问题

插入时需要考虑下面的问题：

因为初始化时，整个数组的每一个元素为空，代表没有头结点。当头插时需要注意防止空指针解引用问题
在扩容时可以采用与开散列相同的思路进行，但是这种方法在当前情况下会有节点释放和创建的损耗，所以采用额外的逻辑进行扩容：将原来的节点重新挂到新的表中

// 数据插入
bool insert(const pair<K, V>& kv)
{
    // 存在时不插入
    if (find(kv.first))
    {
        return false;
    }

    // 扩容
    if (_count == _table.size())
    {
        hashtable h(_table.size() * 2);

        for (size_t i = 0; i < _table.size(); i++)
        {
            Node* cur = _table[i];
            Node* prev = nullptr;
            while (cur)
            {
                Node* next = cur->_next;
                size_t hashi = cur->_kv.first % _table.size();

                cur->_next = h._table[hashi];
                h._table[hashi] = cur;

                cur = next;
            }

            _table[i] = nullptr;
        }

        _table.swap(h._table);
    }

    // 计算存储位置
    size_t hashi = key % _table.size();
    // 链表头插
    Node* newNode = new Node(kv);
    // 找到位置插入
    newNode->_next = _table[hashi];
    // 更新节点，新节点作为头
    _table[hashi] = newNode;
    ++_count;
}

数据查找

思路与开散列基本一致，只是闭散列换成了节点

// 数据查找
Node* find(const K& key)
{
    size_t hashi = key % _table.size();

    Node* cur = _table[hashi];
    while (cur)
    {
        if (cur->_kv.first == key)
        {
            return cur;
        }

        cur = cur->_next;
    }

    return nullptr;
}

数据删除

因为此时是节点，所以不可以直接删除，需要将待删除的节点的下一个与前一个进行链接才能删除

注意此时不可以使用find函数，因为find只能找到删除的节点，但是找不到前一个节点，并且因为没有头结点，所以此时需要考虑头结点的删除和非头结点的删除两种情况

// 数据删除
bool erase(const K& key)
{
    size_t hashi = key % _table.size();
    Node* cur = _table[hashi];
    Node* prev = nullptr;
    while (cur)
    {
        if (cur->_kv.first == key)
        {
            if (cur == _table[hashi])
            {
                // 头结点
                _table[hashi] = cur->_next;
            }
            else
            {
                // 非头结点
                prev->_next = cur->_next;
            }
            delete cur;
            --_count;
            return true;
        }

        prev = cur;
        cur = cur->_next;
    }

    return false;
}

析构函数设计

在开散列时并没有设计析构函数，因为vector会调用自己对应的析构函数，而且vector中的类型也是一个自定义类型会调用对应的析构函数，内置类型不处理，所以可以不用析构函数。但是在闭散列中，每一个哈希数据都是一个在堆上开辟的节点，所以需要额外释放，vector本身的析构函数只能析构_table，不能析构每一个节点

~hashtable()
{
    // 销毁每一个节点
    for (size_t i = 0; i < _table.size(); i++)
    {
        Node* cur = _table[i];
        while (cur)
        {
            Node* toDelete = cur;

            cur = cur->_next;
            delete toDelete;
        }
        _table[i] = nullptr;
    }
}

比较`key`相等以及`key`转`int`仿函数

在前面的代码设计中，如果key本身就是int类型，那么可以直接进行取模操作，但是如果key是浮点类型则上述代码会编译报错，为了解决这个问题，可以引入一个仿函数用于key转int以及比较key相等的仿函数，对于浮点类型、负整型以及指针类型都可以直接强制转换为int类型，但是对于string类型来说，需要采用其他的方法进行处理，这里采用BKDR算法

BKDR算法：用每一个string中的字符的ASCII值乘以31相加的结果作为待映射值

template<class T>
struct Toint
{
    size_t operator()(const T& t)
    {
        return (size_t)t;
    }
};

// 特化
template<>
struct Toint<string>
{
    size_t operator()(const string& t)
    {
        size_t hash = 0;
        for (auto& str : t)
        {
            hash *= 31;
            hash += str;
        }

        return hash;
    }
};

// 修改后的hashtable，以开散列版本为例
// 位置状态
enum Status
{
    Empty,
    Exist,
    Delete
};

// 哈希表每个数据结构
template<class K, class V>
struct HashData
{
    pair<K, V> _kv;
    Status _st = Empty;// 位置状态
};

// 哈希表结构
template<class K, class V, class hash = Toint<K>>
class hashtable
{
public:
    //...
    // 数据插入
    bool insert(const pair<K, V>& kv)
    {
        //...

        hash h;
        // 计算存储位置
        size_t hashi = h(kv.first) % _table.size();
        // ...
    }

    // 数据查找
    HashData<K, V>* find(const K& key)
    {
        hash h;
        // 找到存储位置
        size_t hashi = h(key) % _table.size();
        // ...
    }

    // ...

private:
    vector<HashData<K, V>> _table;// 哈希表
    size_t _count;// 数据个数
};