力扣面试经典算法150题：多数元素

news2024/9/24 10:25:41

多数元素

今天的题目是力扣面试经典150题中的数组的简单题: 多数元素

题目链接：https://leetcode.cn/problems/majority-element/description/?envType=study-plan-v2&envId=top-interview-150

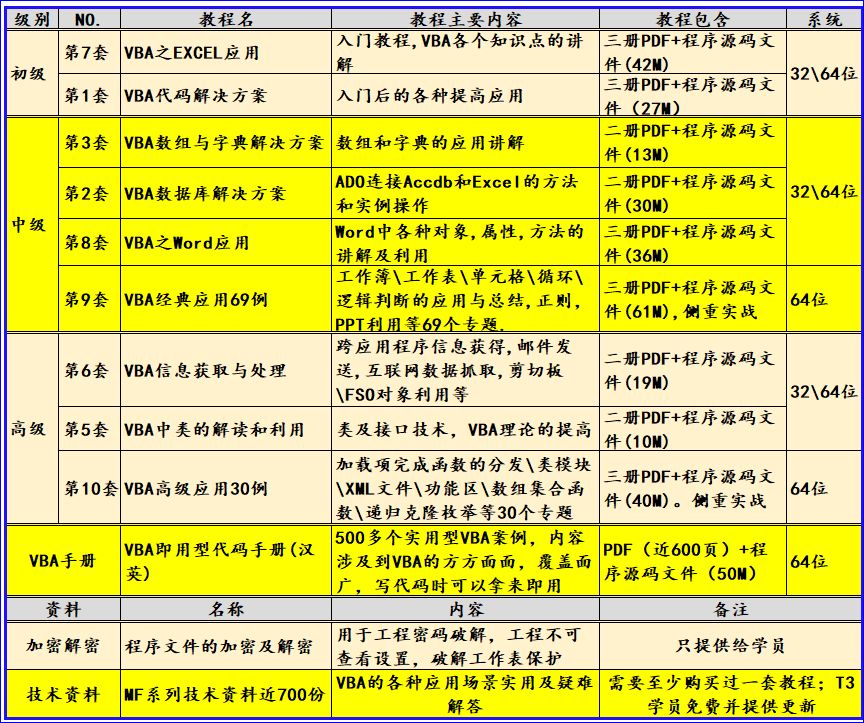
题目描述

给定一个大小为 n 的数组 nums，其中包含 n 个整数，假设有一个元素出现的次数超过 ⌊ n/2 ⌋ 次，则称之为多数元素。
你可以假设数组是非空的，并且给定的数组总是存在多数元素。
请编写一个程序来找出这个多数元素。

注意:
- 数组 nums 的长度为 n。
- 数组中的多数元素出现的次数超过 ⌊ n/2 ⌋ 次。
- 不需要考虑超出新长度以外的元素。
示例:
- 输入:
  nums = [3,2,3]
- 输出:
  多数元素为 3
- 解释:
  数组 nums 中的值 3 出现了两次，超过了一半的次数。
  因此，多数元素为 3。

题目分析

确定目标需求：找出多数元素，即出现次数超过数组长度一半的元素。
提取题目信息：给定一个大小为n的数组nums，也就是说我们已知的条件有两个，一个是数组大小n，这个字段我们用于判断元素是否为多数元素，另外就是数组nums，作为元素来源。
你可以假设数组是非空的，并且给定的数组总是存在多数元素。这段话提示我们，给定的数组必定会存在多数元素。
没有要求不能使用额外空间。

解题思路

没有要求不使用额外空间，那么最容易想到的就是使用map存储元素以及出现次数。

在循环数组时，我们可以同时校验出现次数，因为多数元素是定义超过一半的出现次数，因此这个元素有且只有一个，出现一个即可直接结束循环。

实际算法代码

根据以上分析和思路，我们可以写出以下代码：

public class MajorityElement {
  
    public static void main(String[] args) {
        MajorityElement solution = new MajorityElement();
        
        // 示例数据
        int[] nums = {3, 2, 3};
        
          // 调用查找多数元素方法
        int majorityElement = solution.majorityElementByHash(nums);
        
        // 输出多数元素
        System.out.println("Majority element: " + majorityElement);
    }

	/**
     * 查找多数元素
     *
     * @param nums 输入数组
     * @return 多数元素
     */
    public int majorityElementByHash(int[] nums) {
        // 定义符合条件的目标次数
        int targetCount = nums.length / 2;
        // 定义目标变量
        Integer candidate = null;
        // 定义存储出现次数的map
        Map<Integer, Integer> map = new HashMap<>();
        for (int num : nums) {
            // 当前元素出现的次数,未出现过为0
            Integer count = map.getOrDefault(num, 0);
            // 本次出现,count是历史出现次数
            count++;
            // 当前出现次数大于目标次数,是多数元素,赋值后结束循环
            if (count > targetCount) {
                candidate = num;
                break;
            }else {
                // 不大于目标次数，说明没满足多数元素定义,记录出现次数,继续循环
                map.put(num, count);
            }
        }
        return candidate;
    }

}

执行后满足题目要求：

在这里插入图片描述

提交到力扣也正常通过测试：

在这里插入图片描述

但是事情并没有这么简单。

排序法

题目中说到给定的数组必定有多数元素，而多数元素是出现次数超过数组长度一半的元素。那么假如我给数组排个序，这个元素是不是一定出现在数组中间的位置？

于是有了以下代码：

	--snip--
 	/**
     * 查找多数元素
     *
     * @param nums 输入数组
     * @return 多数元素
     */
    public int majorityElementBySort(int[] nums) {
        // 对数组进行排序
        Arrays.sort(nums);

        // 计算数组的中位数索引
        int midIndex = nums.length / 2;

        // 返回中位数元素
        return nums[midIndex];
    }
    --snip--

启动程序，测试也通过了。

在这里插入图片描述

提交到力扣看看：

在这里插入图片描述

依旧没有问题！

但是事情还是没有这么简单。

摩尔投票法

‌摩尔投票法（Moore’s Voting Algorithm）是一种用于在数组或序列中查找出现次数超过一半的主要元素的算法。这种算法的核心思想是通过不同元素之间的抵消来找到可能的主要元素候选者，并在最后验证候选者是否真正满足要求。摩尔投票法的主要应用场景是寻找数组中的多数元素，即出现次数超过数组长度一半的元素。

算法原理

摩尔投票法的基本思想是通过遍历数组，对每个元素进行投票。当遇到相同的元素时，增加票数；当遇到不同的元素时，减少票数。最终，票数最多的元素即为多数元素。这种算法的关键在于利用不同元素之间的抵消，使得最终剩下的元素成为出现次数最多的候选者。

使用摩尔投票法实现代码如下：


    /**
     * 查找多数元素
     *
     * @param nums 输入数组
     * @return 多数元素
     */
 	public int majorityElement(int[] nums) {
        int count = 0;
        Integer candidate = null;

        // 摩尔投票算法
        for (int num : nums) {
            if (count == 0) {
                candidate = num;
            }
            count += (num == candidate) ? 1 : -1;
            if (count > ( nums.length / 2)) break;
        }
        return candidate;
    }

比较

使用hash的方式属于暴力解题，效率是最低的。排序法和摩尔投票法相对要好一点，所以比较一下：

排序法

优点:
- 简单直观：排序法的实现逻辑简单，易于理解和实现。
- 适用性广：适用于任何类型的数组，无论数组是否有序。
- 确定性：在排序后，多数元素的位置是确定的，位于数组的中间位置。
缺点:
- 时间复杂度较高：排序的时间复杂度通常为 O(n log n)，其中 n 是数组长度。
- 可能的空间开销：虽然大多数现代排序算法都是原地排序，但有些排序算法（如归并排序）需要 O(n) 的额外空间。
- 不适合大数据集：对于非常大的数据集，排序可能会变得非常慢。

摩尔投票法

优点:
- 线性时间复杂度：摩尔投票法的时间复杂度为 O(n)，其中 n 是数组长度。
- 常数空间复杂度：只需要 O(1) 的额外空间。
- 高效：特别适合处理大数据集或实时流数据的情况。
- 无需排序：不需要对数组进行排序，避免了排序带来的额外时间开销。
缺点:
- 理解难度：相对于排序法，摩尔投票法的实现逻辑较为复杂，理解起来可能需要一些时间。
- 适用范围有限：仅适用于存在多数元素的情况，即数组中确实存在一个元素出现次数超过 n/2 的情况。