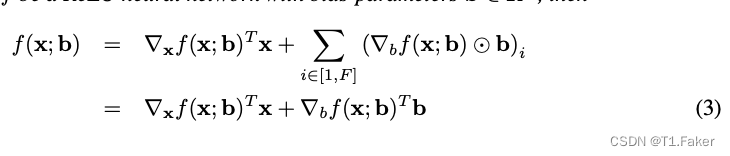昨天面试快手，面试官出了一个cuda编程题–实现前缀和。当时没有做出来，一直在思考是否有类似于规约树这样的解法，感觉好难……面试结束后搜了一下cuda前缀和的介绍，发现该问题是一个经典的cuda编程问题，NVIDIA很早之前就给出了一个快速的实现。看别人的博客研究了很久也没太明白，索性自己写一个好了。
前缀和每一个位置的计算都依赖于前一个位置，这就导致无法利用规约树求和算法逐层递减问题规模。但是前缀和的每一个位置都是从0开始到当前位置的和，总感觉和规约树求和脱不了关系。昨天午休的时候突然灵光一闪，想到了树状数组(BIT)（本篇不会涉及树状数组的基础知识，不了解该数据结构请自行查询。）。树状数组本来的用意是解决单点修改和区间和查询类的问题，说不定可以用到前缀和的计算过程中。

1.利用BIT计算前缀和

先不考虑如何去构造树状数组，假设我们已经构造好了，那我们要计算每一个位置的前缀和，就可以每一个位置启动一个线程去利用BIT查询前缀和，复杂度是O(logN)。每一个位置启动一个线程对cuda来说再容易不过了，所以如果构造好了BIT再去计算前缀和对cuda来说不是难事，那问题的关键就在于如何构造BIT。我们先给出利用BIT计算前缀和的cuda实现：

__global__ static void calc_sum_using_bit(int *input, int *output, int n) {
    int tid = blockIdx.x * blockDim.x + threadIdx.x;

    if (tid < n) {
        output[tid] = 0;
        int idx = tid + 1; //BIT要求索引位置从1开始
        while (idx > 0) {
            output[tid] += input[idx - 1];
            idx -= (idx & -idx); //idx&-idx就是BIT中的lowbit定义
        }
    }
}

2.构造BIT

我看NVIDIA官方实现的paper中，给出了一个它们代码的计算示例图，感觉几乎和BIT一模一样，但是不知道为啥它们没有采用BIT来实现。理解BIT可以在O(logN)时间内求区间和的关键就在于BIT中的每个位置不再是单个元素的值，而可能是一系列元素的和，具体是几个元素的和与该位置二进制中末尾的0个数相关。举个例子，位置7末尾没有0就表示该位置只有其自身，位置8末尾三个0就表示它是前8个元素的和，位置12末尾2个0就表示从12开始前面4个元素的和。利用BIT进行单点修改时，我们会从要修改的位置利用lowbit逐渐往更大的位置修改相关位置的值。假定BIT数组长度为20，我们要增加位置7的值，我们除了要修改位置7之外，还要依次修改位置8、位置16的值。因为在BIT中位置8是前8个元素的和，位置7的值变了前8个元素的和当然也会变化，同理位置16的值也要做相应修改。
既然我们理解了BIT每个位置的含义，那就按照定义去计算每个位置的值就好了。计算方法就如下图所示，第一轮中，我们先更新所有偶数位置：将其值更新为val[pos-1]+val[pos]；在第二轮中，我们再更新所有4倍数的位置，将其更新为val[pos-2]+val[pos]；在第三轮中，我们再更新所有8倍数的位置，将其更新为val[pos-4]+val[pos]，依此类推。大家可以实地去演算一下，每一轮迭代，要计算的位置的值正好符合BIT的定义。

2.1 block内的BIT计算

将BIT的构造用cuda实现还会有一个难题，就是cuda需要考虑block之间的同步，这个问题比较难。虽然cuda 9之后引入了cooperative groups，但是我尝试了一下结果总是不对，无奈放弃。我的解决思路就是分两步走：首先考虑block内的BIT计算，然后再考虑block之间的BIT计算。Block内的BIT计算cuda代码如下：

__global__ static void gen_bit_in_one_block(int *input, int n) {
    int tid = blockIdx.x * blockDim.x + threadIdx.x;

    int idx = 2;
    while (idx <= blockDim.x) {
        if (tid < n && ((tid + 1) & (idx - 1)) == 0) {
            input[tid] += input[tid - (idx >> 1)];
        }
        __syncthreads();
        idx <<= 1;
    }
}

上述代码，如果将while循环改成while(idx <= n)那就是完整的BIT计算，但是在cuda中是不正确的，因为没有考虑块间同步，如果能很好地解决块间同步，则可以直接一个kernel完成BIT的构造。idx表示当前的BIT每个位置从该位置开始要计算的前缀和长度。__syncthreads不能少，因为后面位置的计算会依赖于前面位置的结果，所以必须要保证一个block之内的线程同步。

2.2 block之间的BIT计算

Block之间的BIT计算有两种方案。第一种方案是将块间同步通过kernel调用来实现，将kernel包在while循环中完成BIT的构造，代码如下：

__global__ static void gen_bit_one_layer(int *input, int n, int idx) {
    int tid = blockIdx.x * blockDim.x + threadIdx.x;
    if (tid < n && ((tid + 1) & (idx - 1)) == 0) {
        input[tid] += input[tid - (idx >> 1)];
    }
}

但是当元素较多时，kernel调用次数会比较多，从而影响速度。第二种方案是启动一个block完成块间BIT的计算，代码如下：

__global__ static void gen_bit_between_blocks(int *input, int n, long long idx) {
    int tid = threadIdx.x;
    while (idx <= n) {
        for (long long pos = (tid + 1) * idx; pos <= n; pos += idx * blockDim.x) {
            input[pos - 1] += input[pos - 1 - (idx >> 1)];
        }
        __syncthreads();
        idx <<= 1;
    }
}

调用上述几个核函数的完整代码如下：

inline int get_block_size(int size, int block_size) { 
	return (size + block_size - 1) / block_size;
}
void calc_prefix_sum(int *input, int *output, int n) {
	// copy from cpu to gpu .....

    dim3 dimBlock(256);
    dim3 dimGrid(get_block_size(n, 256));

    gen_bit_in_one_block<<<dimGrid, dimBlock>>>(buffer1, n);

    int idx = 512;
#if 0
    // 元素很多时需要迭代很多轮，速度慢于下面的实现
    while (idx < n) {
        gen_bit_one_layer<<<dimGrid, dimBlock>>>(buffer1, n, idx);
        idx <<= 1;
    }
#else
    gen_bit_between_blocks<<<1, dimBlock>>>(buffer1, n, idx);
#endif
    calc_sum_using_bit<<<dimGrid, dimBlock>>>(buffer1, buffer2, n);
    cudaDeviceSynchronize();
   
	// copy from gpu to cpu .....
}

3.性能

从网上搜到一个最近的开源实现《Parallel Prefix Sum (Scan) with CUDA》，此实现仿照nvidia官方paper对前缀和进行了优化，我们与其进行速度对比。我的电脑CPU是8核AMD Ryzen 7 5800X，GPU是NVIDIA GeForce RTX 3070，表中耗时单位是ms。

	100	1000	1万	10万	100万	1000万	1亿	10亿
cpu	0	0	0.01	0.07	0.58	4.56	40	406
gen_bit_one_layer	0.02	0.02	0.03	0.05	0.14	1.16	12.5	128
gen_bit_between_blocks	0.02	0.02	0.02	0.03	0.10	0.80	8.2	79
开源bcao	0.02	0.02	0.04	0.05	0.13	0.68	6.1	54

当元素个数小于5万时CPU上最快，小于300万时我的代码会最快，大于300万时开源代码最快，但是差距没有拉开很多。不过，从代码量上来说我的实现代码量要比开源实现小很多，理解也会更容易。如果能将BIT的构造都在一个kernel中实现，速度有机会更进一步，等将来熟悉cooperative groups之后再去尝试。当然，前缀和问题本来就是一个O(n)的问题，复杂度很低，所以CPU实现也能比较快得处理大规模数据，GPU并没有加速很多。但是cuda版的前缀和还是有价值的，尤其在一个需要很多GPU操作的项目中可以避免将数据拷回CPU进行处理。