导语
这篇论文介绍了一种新的工具,称为全梯度,用于解释神经网络的响应。这个全梯度的概念将神经网络的响应分解为两个部分:输入灵敏度和每个神经元的灵敏度分量。
- 输入灵敏度:输入灵敏度指的是对于神经网络输出的影响程度。它反映了输入数据的不同部分对于神经网络输出的重要性。通过计算输入数据相对于神经网络输出的梯度,可以得到每个输入数据的灵敏度值,即该数据对于最终输出的贡献程度。较高的输入灵敏度值表示该输入数据在决定输出方面起着重要作用。
- 每个神经元的灵敏度分量:每个神经元的灵敏度分量指的是该神经元对于神经网络输出的影响程度。它反映了神经网络中每个神经元在输出方面的贡献。通过分解神经网络输出相对于每个神经元的梯度,可以得到每个神经元的灵敏度分量。较高的灵敏度分量表示该神经元在决定输出方面起着重要作用
对于卷积网络,论文提出了一种近似显着图表示,称为 FullGrad,是通过聚合全梯度分量获得。
博主自己的理解就是有点类似于传统图像处理梯度算法,例如Sobel基本上改为卷积处理,也可以理解为研究用于解释神经网络函数的显着图表示。
其中显着图为每个输入特征分配一个重要性分数,这是该特征对于神经网络执行的任务的有用性的度量。然而,特征之间存在内部结构,有时使得很难为每个特征分配单个重要性分数。例如,诸如自然图像之类的输入空间本质上是组合的。这意味着,虽然图像中的任何单个像素本身可能并不重要,但如果像素集合形成重要的图像区域(例如对象部分),则它们可能至关重要。
比如说,如果丢失任何单个像素,图像中的自行车仍然可以被识别,但如果与关键元素(例如车轮或传动链)对应的整个像素集合丢失,那么识别就会变得更加困难
显著图解释
虽然显着性没有单一的正式定义,但社区认为有几个重要的直观特征
- 如果输入特征的变化极大地影响神经网络的输出,那么这个特征就必须被视为重要。
- 另一个理想的特性是显著性图必须完全解释神经网络的输出,即各个特征的重要性得分必须加起来等于神经网络的输出。这一点可以通过重新分配数字输出分数给各个输入特征来实现。换句话说,如果一个特征对输出做出了很大的数值贡献,那么它就很重要。
然而,我们面临着一个挑战:对于实际的神经网络来说,局部归因和全局归因这两种概念几乎总是会产生截然不同的特征集认为是重要的。
- 局部归因强调的是在局部范围内的重要性,即某个特征在某个具体的任务中的贡献程度;
- 而全局归因则更注重整体的重要性,考虑的是各个特征在整个神经网络中的贡献程度。这种差异有时会让人感到困惑,因为它违反了我们直觉上对于重要性的理解
正是如此,论文才提出了全梯度,一种为神经网络中的输入特征和单个特征检测器(或神经元)分配重要性分数的表示。输入归因有助于捕获单个输入像素的重要性,而神经元重要性捕获像素组的重要性,并解释其结构。此外,全梯度通过同时满足局部和全局重要性的概念来实现这一点。
本地和全局归因概念的显著图
在神经网络中的本地归因(Local Attribution)和全局归因(Global Attribution)是两种用于解释和理解模型决策的解释性方法,特别是在可解释性显著图(saliency maps)中广泛应用
这里阐述一个理论点:不存在同时满足本地和全局归因概念的显著图
以下是对这两个概念的详细解释:
本地归因(Local Attribution)
- 含义:
-
- 本地归因关注的是单个输入样本对于模型输出的影响。换句话说,本地归因方法试图回答“对于给定的输入样本,模型是如何得出这个具体的预测结果的?”
-
- 在显著图的上下文中,本地归因试图确定输入的哪些部分(如图像中的像素)对模型输出有最大影响。
- 公式:
-
- 对于本地归因,常用的方法之一是梯度显著图(Gradient-based Saliency Map)。给定模型
f
f
f和输入
x
x
x,梯度显著图可以通过计算模型输出相对于输入的梯度来得到:
S a l i e n c y M a p = ∂ f ( x ) ∂ x Saliency Map = \frac{∂f(x)}{∂x} SaliencyMap=∂x∂f(x)
这里,梯度值的绝对值表示每个输入元素(如像素)对模型输出的贡献度。高梯度值的区域表明这些区域对模型决策的影响较大。
- 对于本地归因,常用的方法之一是梯度显著图(Gradient-based Saliency Map)。给定模型
f
f
f和输入
x
x
x,梯度显著图可以通过计算模型输出相对于输入的梯度来得到:
全局归因(Global Attribution)
- 含义:
-
- 全局归因则是关注整个输入数据集上的特征如何影响模型输出。它试图回答“整体来看,哪些输入特征对模型的预测最为重要?”。
-
- 全局归因方法提供了模型对输入特征重要性的总体理解,而不是仅针对某一个特定样本。
- 公式:
-
- 一个常见的全局归因方法是SHAP(SHapley Additive exPlanations)值。SHAP 值基于博弈论的 Shapley 值,量化每个特征对模型预测的贡献。给定输入特征集
X
=
{
x
1
,
x
2
,
.
.
.
,
x
n
}
X=\lbrace x_1,x_2,...,x_n\rbrace
X={x1,x2,...,xn},SHAP 值
ϕ
i
\phi_i
ϕi对应特征
x
i
x_i
xi的归因计算为:
ϕ i ( f , x ) = ∑ S ⊆ X ∖ x i ∣ S ∣ ! ( ∣ X ∣ − ∣ S ∣ − 1 ) ! ∣ X ∣ ! [ f ( S ∪ { x i } ) − f ( S ) ] \phi_i(f,x)=\sum_{S\subseteq X \setminus{x_i}}\frac{|S|!(|X|-|S|-1)!}{|X|!}[f(S \cup \lbrace x_i \rbrace) -f(S)] ϕi(f,x)=S⊆X∖xi∑∣X∣!∣S∣!(∣X∣−∣S∣−1)![f(S∪{xi})−f(S)]
这里, S S S 表示特征子集,而 f ( S ) f(S) f(S) 表示模型在特征子集 S S S上的输出。这一计算涉及所有可能的特征组合,综合了每个特征的边际贡献。
- 一个常见的全局归因方法是SHAP(SHapley Additive exPlanations)值。SHAP 值基于博弈论的 Shapley 值,量化每个特征对模型预测的贡献。给定输入特征集
X
=
{
x
1
,
x
2
,
.
.
.
,
x
n
}
X=\lbrace x_1,x_2,...,x_n\rbrace
X={x1,x2,...,xn},SHAP 值
ϕ
i
\phi_i
ϕi对应特征
x
i
x_i
xi的归因计算为:
总结就是本地和全局归因的显著图就是用来解释神经网络如何做出决策的图像。本地归因是关注于在某个具体任务中,每个输入特征对结果的影响程度;而全局归因则是考虑整个神经网络中每个特征对结果的总体影响。这些图像帮助我们了解神经网络如何利用输入数据做出决策。
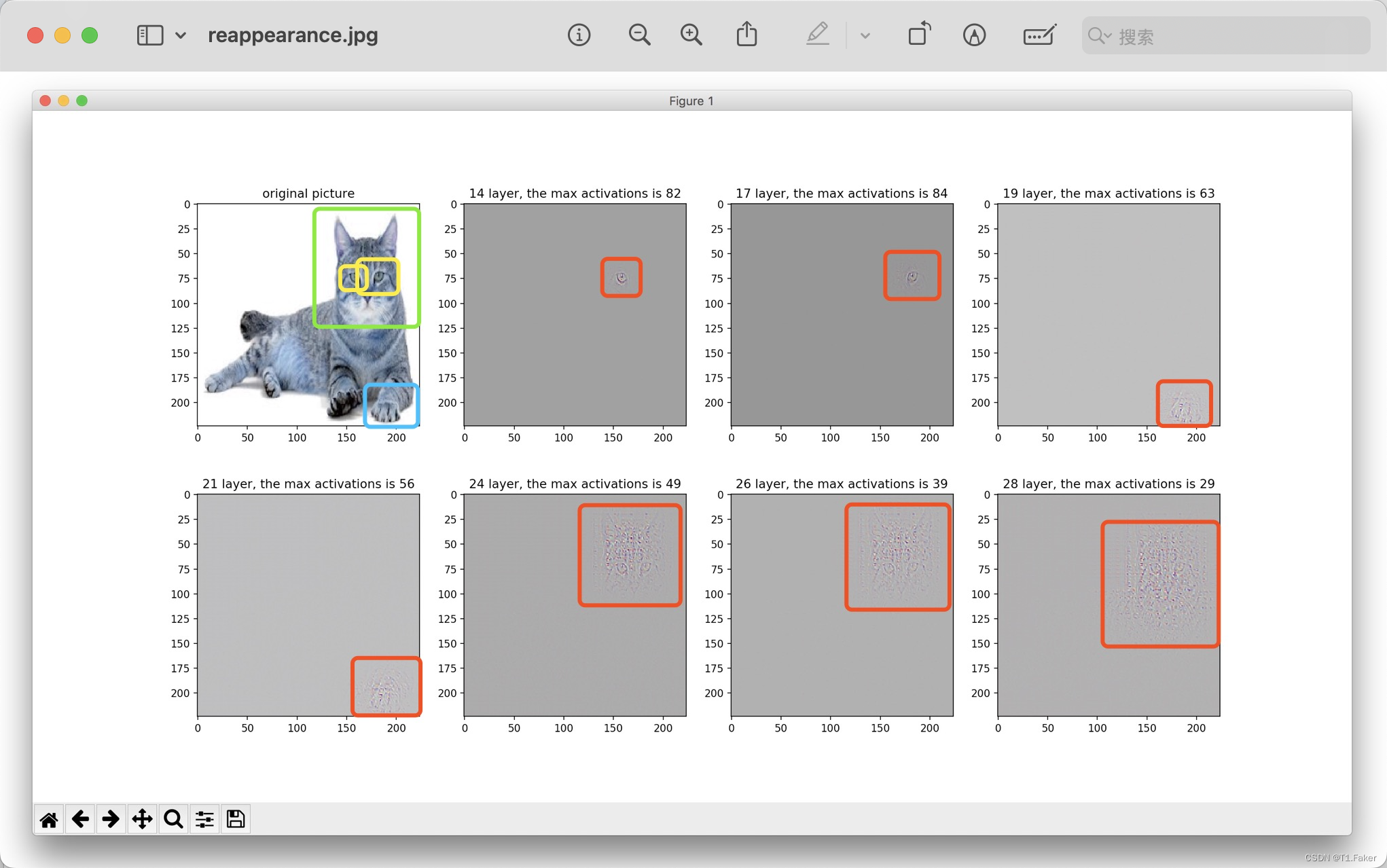
另外在 D D D维空间中的显著图无法完整描述线性模型的行为,因为线性模型除了 D D D个权重参数外,还有一个额外的偏置项,使得模型总共有 D + 1 D+1 D+1个参数。而显著图通常仅反映了输入特征的权重,忽略了偏置项对模型输出的影响。
下面将通过定义局部归因的弱概念(称为弱依赖性)和全局归因的弱概念(称为完整性)来证明这个的结果。我们将通过先定义显著图,再通过命题推论的方法来实现。
假设我们有一个神经网络函数,现在考虑一个带有输入 x ∈ R D x \in R^D x∈RD的神经网络函数 f : R D → R f:R^D \rightarrow R f:RD→R
显著图 S ( x ) = σ ( f , x ) ∈ R D S(x) =\sigma(f,x) \in R^D S(x)=σ(f,x)∈RD是神经网络 f f f和输入 x x x的函数。对于 f ( x ) = w T x + b f(x)=w^Tx+b f(x)=wTx+b形式的线性模型。通常将权重可视化 w w w。对于这种情况,通过反梯度,观察到显著图 S ( x ) = w S(x)=w S(x)=w独立于 x x x,
类似地,分段线性模型可以被认为是线性模型的集合,每个线性模型都在不同的局部邻域上定义。对于这种情况,我们可以如下定义弱依赖。
定义1:(对输入的弱依赖)考虑分段线性模型
f ( x ) = { w 0 T x + b 0 , x ∈ μ 0 . . . w n T x + b n , x ∈ μ n f(x)= \begin{cases} w_0^Tx+b_0,\quad x\in \mu_0\\ ... \\ w_n^Tx+b_n, \quad x\in \mu_n \end{cases} f(x)=⎩ ⎨ ⎧w0Tx+b0,x∈μ0...wnTx+bn,x∈μn
其中所有 u i u_i ui 都是开连接的集合。对于这个函数,限制在集合 u i u_i ui 上的显著图 S ( x ) = σ ( f , x ) S(x) = σ(f, x) S(x)=σ(f,x) 不依赖于 x x x,并且仅依赖于参数 w i w_i wi, b i b_i bi。
定义2:完整性显著图 S ( x ) S(x) S(x)
- 如果我们能够找到一个函数 ϕ \phi ϕ,让它通过输入显著图 S ( x ) S(x) S(x)和输入 x x x,就可以恢复模型 f f f对 x x x的输出值 f ( x ) f(x) f(x),那么我们就说这个显著图是“完整的”。也就是说,显著图包含了足够的信息,可以准确还原模型的输出。
- 如果我们能够找到一个函数 ϕ \phi ϕ,使得给定显著图 S ( x ) S(x) S(x)、基线点 x 0 x_0 x0的显著图 S 0 ( x 0 ) S_0(x_0) S0(x0)、输入 x x x和基线点 x 0 x_0 x0,我们就可以计算出模型输出的差值 f ( x ) − f ( x 0 ) f(x) − f(x_0) f(x)−f(x0),即 ϕ ( S ( x ) , S 0 ( x 0 ) , x , x 0 ) = f ( x ) − f ( x 0 ) \phi(S(x), S_0(x_0), x, x_0) = f(x) − f(x_0) ϕ(S(x),S0(x0),x,x0)=f(x)−f(x0),那么显著图 S ( x ) S(x) S(x)就是相对于基线 x 0 x_0 x0“完整的”。这个定义更为通用,因为它不仅考虑了单一的输入,还考虑了相对于一个基线点的变化。
在这两种情况下,假设 ϕ \phi ϕ 不是 S ( x ) S(x) S(x) 的常数函数( ϕ \phi ϕ必须是一个依赖于 S ( x ) S(x) S(x)的非常数函数。也就是说, ϕ \phi ϕ不能仅仅是一个固定值或常数,它必须根据 S ( x ) S(x) S(x)的变化而变化。
如果显著图 S ( x ) S(x) S(x)能够完整地记录模型 f f f的计算过程,那么我们就应该能够通过显著图和输入 x x x来准确还原出模型的输出 f ( x ) f(x) f(x)。
根据上面的定义,接下来我们来推论我们的猜想命题。
命题1:对于任何分段线性函数 f f f ,在大多数情况下,我们无法同时构建一个显著图 S S S,使得这个显著图既能够完全表达出函数 f f f 的行为(即满足“完备性”),又能够对输入的变化保持弱依赖性(即对输入的变化不敏感)。
诸如集成梯度(Integrated Gradients)、深度泰勒分解(Deep Taylor Decomposition)和 DeepLIFT 等方法虽然满足完备性。但不满足对输入的弱依赖性。
这里我们给定一个基线。给定基线 x ′ x^\prime x′ ,积分梯度 ( I G ) (IG) (IG) 由 I G i ( x ) = ( x i − x i ′ ) × ∫ α = 0 1 ∂ f ( x ′ + α ( x − x ′ ) ) ∂ x i d α IG_i(x)=(x_i-x^\prime_i) \times \int^1_{\alpha=0}\frac{\partial f(x^\prime+\alpha(x-x^\prime))}{\partial x_i}d\alpha IGi(x)=(xi−xi′)×∫α=01∂xi∂f(x′+α(x−x′))dα给出,其中 x i x_i xi是 i t h i^{th} ith输入坐标。
示例 1
考虑输入 ( x 1 , x 2 ) ∈ R 2 (x_1,x_2)\in R^2 (x1,x2)∈R2的分段线性函数。
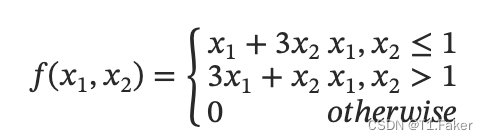
假设基线 x ′ = ( 0 , 0 ) x^\prime=(0,0) x′=(0,0)。考虑三个点 ( 2 , 2 ) , ( 4 , 4 ) , ( 1.5 , 1.5 ) (2,2),(4,4),(1.5,1.5) (2,2),(4,4),(1.5,1.5),所有这些都
满足 x 1 , x 2 > 1 x_1,x_2>1 x1,x2>1 ,因此受到 f ( x 1 , x 2 ) = 3 x 1 + x 2 f(x_1,x_2)=3x_1+x_2 f(x1,x2)=3x1+x2相同的线性函数的影响。
然而,根据我们考虑的点, I G IG IG在输入特征之间产生不同的相对重要性。
根据积分梯度算出
I
G
(
x
1
=
4
,
x
2
=
4
)
=
(
10
,
6
)
IG(x_1=4,x_2=4)=(10,6)
IG(x1=4,x2=4)=(10,6)似乎
x
1
x_1
x1更重要(如10>6 )。
而对于
I
G
(
1.5
,
1.5
)
=
(
2.5
,
3.5
)
IG(1.5,1.5)=(2.5,3.5)
IG(1.5,1.5)=(2.5,3.5) ,似乎
x
2
x_2
x2更重要。
此外,在 I G ( 2 , 2 ) = ( 4 , 4 ) IG(2,2)=(4,4) IG(2,2)=(4,4)处,两个坐标被赋予同等重要性。然而,在所有三种情况下,输出显然对 x 1 x_1 x1的更改比对 x 2 x_2 x2的更改更敏感,因为它们位于 f ( x 1 , x 2 ) = 3 x 1 + x 2 f(x_1,x_2)=3x_1+x_2 f(x1,x2)=3x1+x2上,因此,积分梯度在某些情况下会给出与我们直觉不符的归因结果。
由此可见,弱依赖性和完整性这两个直观性质不能同时满足。
为什么会出现这种矛盾?
这是因为在计算显著图时,我们只关注了输入特征的梯度,而忽略了偏置项的影响。对于简单的线性模型,忽略偏置项可能不会有太大影响,但对于复杂的神经网络模型,每个神经元的偏置项会产生显著影响,而这些影响无法通过传统的显著图方法来捕捉。这也是为什么我们在很多情况下会发现显著图给出的特征重要性与实际模型行为之间存在不一致的原因。
在下一节中,我们将研究全梯度,它是比显着图更具表现力的工具,可以解释偏差项并满足弱依赖性和完整性。
完全梯度表示
在这一部分,我们将介绍这个称为完全梯度表示的方法,这种方法用于分析神经网络的输出,它能更全面地解释网络的行为。这是因为它不仅考虑了输入的梯度变化,还包括了偏置项的影响。
基本概念
我们首先从一个简单的情况出发,即没有偏置参数的 ReLU 神经网络。对于这种网络,可以证明以下命题:
命题 2: 设 f f f 是一个没有偏置参数的 ReLU 神经网络,那么 f ( x ) = ∇ x f ( x ) T x f(x) = \nabla_x f(x)^T x f(x)=∇xf(x)Tx。
解释: 这个命题告诉我们,对于一个没有偏置参数的 ReLU 网络,输出 f ( x ) f(x) f(x) 可以表示为输入 x x x 和其对应的梯度 ∇ x f ( x ) \nabla_x f(x) ∇xf(x) 的内积。梯度 ∇ x f ( x ) \nabla_x f(x) ∇xf(x) 表示网络输出对输入每个分量的敏感性。
为什么成立: 这个命题的证明基于一个重要性质:对于任意的常数 k > 0 k > 0 k>0,如果将输入放大 k k k 倍,那么输出也会相应地放大 k k k 倍,即 f ( k x ) = k f ( x ) f(kx) = kf(x) f(kx)=kf(x)。这表明网络的输出与输入的比例关系是线性的。这种性质通常被称为齐次性。
推广: 通过在网络中引入额外的输入项,可以将这种性质推广到带有偏置参数的 ReLU 神经网络。这种方法类似于在分析线性模型时,向模型中添加一个常数项。
带偏置的完全梯度表示
对于带有偏置参数的 ReLU 神经网络 f ( x ; b ) f(x; b) f(x;b),其中 b b b 是偏置向量,情况变得稍微复杂一些。我们可以提出如下命题:
命题 3: 设 f f f 是一个带有偏置 b ∈ R F b \in \mathbb{R}^F b∈RF 的 ReLU 神经网络,那么
f ( x ; b ) = ▽ x f ( x ; b ) T x + ▽ b f ( x ; b ) T b f(x;b) = \bigtriangledown_xf(x;b)^Tx+\bigtriangledown_bf(x;b)^Tb f(x;b)=▽xf(x;b)Tx+▽bf(x;b)Tb
解释: 这个公式表达的是,神经网络的输出可以被精确地分解为两部分:一部分是输入梯度 ∇ x f ( x ; b ) \nabla_x f(x;b) ∇xf(x;b) 和输入 x x x 的内积,另一部分是偏置梯度 ∇ b f ( x ; b ) \nabla_b f(x;b) ∇bf(x;b) 和偏置 b b b 的内积。
进一步理解: 输入梯度 ∇ x f ( x ; b ) \nabla_x f(x;b) ∇xf(x;b) 捕捉了网络输出对输入变化的敏感性,也就是当输入发生微小变化时,输出如何响应。偏置梯度 ∇ b f ( x ; b ) \nabla_b f(x;b) ∇bf(x;b) 则反映了偏置参数对输出的影响。将这两个部分结合起来,我们就得到了完全的梯度表示。
偏置的扩展表示
在实际应用的神经网络中,除了显式的偏置参数(即模型中明确列出的偏置)之外,还存在一些隐式偏置。隐式偏置包括批量归一化层的运行平均值等。这些隐式偏置虽然在模型结构中没有直接体现,但对模型的行为有着显著的影响。
进一步解释: 研究表明,这些隐式偏置的影响通常远大于显式偏置。因此,在解释神经网络的行为时,必须将它们考虑在内。
为了更加全面地理解偏置的作用,我们可以将这种分解扩展到一般情况下,考虑使用通用非线性激活函数 σ ( x ) \sigma(x) σ(x) 产生的隐式偏置。
假设 y = σ ( x ) y = \sigma(x) y=σ(x) 表示激活函数的输出,那么我们可以将其表示为:
y = d σ ( x ) d x x + b σ y=\frac{d\sigma(x)}{dx}x+b_\sigma y=dxdσ(x)x+bσ
解释: 这里的 b σ b_\sigma bσ 是由于激活函数的非线性而产生的隐式偏置项。对于类似 ReLU 这样的非线性函数,这个偏置项 b σ b_\sigma bσ 通常为零,但对于其他类型的非线性激活函数,它可能不为零。
应用: 我们可以通过将 b σ b_\sigma bσ 添加到偏置向量 b b b 中,将完全梯度表示方法扩展到具有任意非线性激活函数的神经网络中。这使得我们能够更加全面地分析和解释神经网络的行为,尤其是在处理复杂的非线性模型时。
完全梯度的性质
在我们理解了完全梯度的基本概念之后,接下来讨论其一些关键性质,这些性质进一步揭示了完全梯度表示的优势和应用。
这里讨论完全梯度的一些直观性质。我们将假设完全梯度由对 G = ( ▽ x f ( x ) , f b ( x ) ) ∈ R D + F G=(\bigtriangledown_xf(x),f^b(x)) \in R^{D+F} G=(▽xf(x),fb(x))∈RD+F的一对组成。我们还假设在不失一般性的情况下,网络包含不带批归一化的 ReLU 非线性,并且所有的偏置都是由偏置参数引起的。
输入依赖性弱:
对于分段线性函数 f f f,输入梯度在线性区域内是局部恒定的。类似地,完全梯度的偏置部分 f b ( x ) f^b(x) fb(x) 也具有类似的性质,这使得完全梯度在处理线性区域时表现出一致性。具体的证明可以在补充材料中找到。
完整性:
根据命题 3,完全梯度可以完整恢复函数输出
f
(
x
)
f(x)
f(x),这保证了其完整性。完全梯度的这种性质确保了我们可以从输入和偏置的梯度中准确地重建网络的输出。
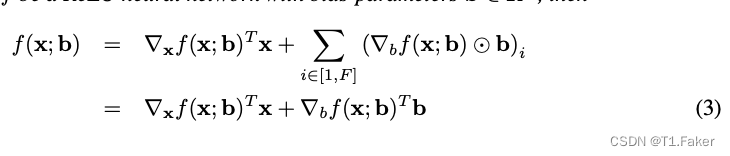
饱和敏感性:
“饱和”指的是在某些情况下,对零函数梯度区域的归因现象。一个例子是函数 f ( x ) = a − ReLU ( b − x ) f(x) = a - \text{ReLU}(b - x) f(x)=a−ReLU(b−x),在 x = 2 x = 2 x=2 时,即使 f ( x ) = 1 f(x) = 1 f(x)=1,输入的归因也为零。这种现象被认为是反直觉的。传统的方法,如 Integrated Gradients 和 DeepLIFT,引入了基线输入来解决这个问题,但基线的选择仍然依赖于输入。完全梯度方法通过同时考虑偏置参数,提供了更全面的解决方案。例如,对于函数 f ( x ) f(x) f(x),完全梯度方法将偏置对输入的归因为 ( 1 , 0 ) (1, 0) (1,0),使得处理饱和问题更加直观。
完全对函数映射敏感:
Adebayo 等人提出了一些显著图需要满足的合理性标准,包括显著图必须对模型参数的随机化敏感。具体而言,显著图必须能够反映参数变化对函数映射的影响。与输入梯度方法不同,完全梯度对所有参数的变化均敏感。即,完全梯度方法能够准确地捕捉由参数变化引起的函数映射变化。
示例 2: 考虑形式为 f ( x ) = w 1 ⋅ ReLU ( w 0 ⋅ x + b 0 ) + b 1 f(x) = w_1 \cdot \text{ReLU}(w_0 \cdot x + b_0) + b_1 f(x)=w1⋅ReLU(w0⋅x+b0)+b1 的网络。在这个例子中,输入梯度对 b 0 b_0 b0 的变化不敏感,但对 b 1 b_1 b1 的变化非常敏感。完全梯度则对所有参数的变化都敏感,这使得它在处理模型随机化测试时更具优势。
FullGrad:卷积网络的完全梯度显著图
在深度学习中,尤其是处理图像数据时,理解卷积神经网络(CNN)如何对输入图像的不同部分进行特征提取和重要性评估是至关重要的。FullGrad方法作为一种可视化技术,通过利用卷积层中的偏置梯度来生成空间显著图,为这一理解提供了有力工具。下面,我们将详细解析FullGrad方法,并结合相关术语和概念进行优化阐述。
偏置梯度与空间显著图
在CNN中,每个卷积层由多个卷积滤波器组成,这些滤波器通过滑动窗口的方式在输入特征图上滑动,执行局部特征提取。每个滤波器包含一个权重矩阵(或向量)和一个偏置项。尽管偏置项在单个滤波器中是共享的(即对所有位置应用相同的值),但其在梯度反向传播过程中的表现却具有独特的空间结构。
对于给定的卷积滤波器 z = w ∗ x + b z=w∗x+b z=w∗x+b,其中 w ∈ R 2 k + 1 w∈R^{2k+1} w∈R2k+1是权重向量, b b b是重复了 D D D次的单个标量偏置(假设输出特征图大小为 D),偏置梯度 f b ( x ) = ∇ z f ( x ) ⋅ b f^b(x)=∇_z f(x)⋅b fb(x)=∇zf(x)⋅b能够揭示出哪些输入位置对输出有重要影响。由于偏置梯度的形状与输$ x x x相似,因此可以像处理输入图像一样直接可视化,从而生成所谓的空间显著图。
FullGrad显著图的生成
FullGrad方法通过聚合多个层级的偏置梯度显著图来生成一个全局显著图,从而提供更全面的视觉解释。具体步骤如下:
- 神经元级映射:首先,为网络中的每个卷积滤波器生成一个空间映射,这些映射反映了该滤波器对应输入区域的显著性。
- 层级聚合:然后,将同一层内所有通道的显著图进行聚合,得到该层的显著图。聚合方法可以是简单的求和或其他加权方式。
- 全局聚合:最后,将不同层的显著图进一步聚合,生成整个网络的全局显著图。这一步骤中,通常会考虑使用插值等后处理手段来确保最终显著图与输入图像具有相同的空间分辨率。
在FullGrad显著图的生成公式中:
S f ( x ) = ψ ( ∇ x f ( x ) x ) + ∑ l ∈ L ∑ c ∈ c l ψ ( f b ( x ) c ) ( 2 ) S_f(x) = \psi(\nabla_x f(x) x) + \sum_{l \in L} \sum_{c \in cl} \psi(f^b(x)_c) (2) Sf(x)=ψ(∇xf(x)x)+l∈L∑c∈cl∑ψ(fb(x)c)(2)
- ∇ x f ( x ) x \nabla_x f(x) x ∇xf(x)x表示输入 x x x相对于输出 f ( x ) f(x) f(x) 的梯度与输入的乘积,反映了输入本身对输出的影响。
- f b ( x ) c f^b(x)_c fb(x)c表示第 l 层中第 c 个通道的偏置梯度显著图。
- ψ(⋅) 是后处理函数,用于调整显著图的视觉效果,如通过绝对值操作忽略符号,通过线性缩放和双线性插值调整大小和分辨率。
优点与局限性
FullGrad方法的主要优点在于它能够结合输入梯度和偏置梯度来生成更加全面的显著图,从而更准确地反映网络对输入图像不同部分的关注程度。然而,该方法也存在一些局限性:
- 近似性:FullGrad显著图是近似的,因为它试图从多个映射中捕获信息到一个单一的视觉连贯的显著图中,这可能导致信息的丢失或扭曲。
- 无法完全考虑全连接层:对于同时包含卷积层和全连接层的网络,FullGrad方法只能获得卷积层的空间映射,无法完全利用全连接层的偏置参数。