图的基本概念

图(Graph)是由顶点集合及顶点间的关系组成的一种数据结构：$G=(V,E)$，其中：

• 顶点集合 V = { x ∣ x 属 于 某 个 数 据 对 象 集 } V=\{x|x属于某个数据对象集\} V={x∣x属于某个数据对象集} 是有穷非空集合
• E = { ( x , y ) ∣ x , y ∈ V } E=\{(x,y)|x,y\in V\} E={(x,y)∣x,y∈V} 或者 E = { ⟨ x , y ⟩ ∣ x , y ∈ V ∧ P a t h ( x , y ) } E=\{\langle x,y\rangle|x,y\in V\wedge \rm{Path}(x,y)\} E={⟨x,y⟩∣x,y∈V∧Path(x,y)}

如下，是各种图的可视化表示

其中的G2是一棵树，树是一种特殊的图（无环、连通）

在研究树的时候，我们关注的是结点中存的值，而研究图，我们要不光要关注结点，还要关注边的权值。

G1 和 G2 都是无向图，G3 和 G4 都是有向图

• 完全图：任意两个顶点之间都直接相连，是最稠密的图
  • 在 $n$ 个顶点的无向图中，若有 $\frac{n\times (n-1)}{2}$ 条边，即任意两个顶点之间有且仅有一条边，则称此图为 无向完全图，如上图 $G1$。
  • 在 $n$ 个顶点的有向图中，若有 $n\times (n-1)$ 条边，即任意两个顶点之间有且仅有方向相反的边，则称此图为 有向完全图，如上图 $G4$。
• 邻接顶点：
  • 在无向图 $G$ 中，若 $(u,v)$ 是 $E(G)$ 中的一条边，则称 $u$ 和 $v$ 互为邻接顶点，并称边 $(u,v)$ 依附于顶点 $u$ 和 $v$。
  • 在有向图 $G$ 中，若 $⟨u,v⟩$ 是 $E(G)$ 中的一条边，则称顶点 $u$ 邻接到顶点 $v$，顶点 $v$ 邻接自顶点 $u$，并称边 $⟨u,v⟩$ 与顶点 $u$ 和顶点 $v$ 相关联。
• 顶点的度：
  • 顶点 $v$ 的度是指与它相关联的边的条数，记作 $d(v)$
  • 在有向图中，顶点的度等于该顶点的出度和入度之和，其中顶点 $v$ 的出度是以 $v$ 为起始点的有向边的条数，记作 $d^{+}(v)$；顶点 $v$ 的入度是以 $v$ 为终点的边的条数，记作 $d^{-}(v)$，显然 $d(v)=d^{+}(v)+d^{-}(v)$
• 路径：在图 $G=(V,E)$ 中，若从顶点 $v_i$ 出发有一组边使其可以到达顶点 $v_j$，则称顶点 $v_i$ 到顶点 $v_j$ 的顶点序列为从顶点 $v_i$ 到顶点 $v_j$ 的路径。
• 路径长度：
  • 对于不带权的图，一条路径的长度是指该路径上的边的条数。
  • 对于带权的图，一条路径的长度是指该路径上各个边权值的和。
• 简单路径与回路：若一条路径 $v_1,v_2,v_3,\cdots ,v_m$ 上的各个顶点均不重复，则这样的路径称为简单路径。若路径上第一个顶点 $v_1$ 和最后一个顶点 $v_m$ 重合，则称这样的路径为回路或环。
• 子图：设图 G = { V , E } G=\{V,E\} G={V,E} 和图 G 1 = { V 1 , E 1 } G_1=\{V_1,E_1\} G1​={V1​,E1​}，若 $V_1\in V\wedge E_1\in E$，则称 $G_1$ 是 $G$ 的子图
• 连通图：在无向图中，若从顶点 $v_1$ 到顶点 $v_2$ 有路径，则称顶点 $v_1$ 与顶点 $v_2$ 是连通的。如果图中任一对顶点都是连通的，则称此图为连通图。
• 强连通图：在有向图中，若在每一对顶点 $v_i$ 和 $v_j$ 之间都存在一条从 $v_i$ 到 $v_j$ 的路径，也存在一条从 $v_j$ 到 $v_i$ 的路径，则称此图为强连通图。
• 生成树：在无向图中，一个连通图的最小连通子图称为该图的生成树。有 $n$ 个顶点的连通图的生成树有 $n$ 个顶点和 $n-1$ 条边。

图的存储结构

图的存储主要有两方面，存储结点和边（结点与结点之间的关系），结点只需要用数组存储即可，而边怎么存呢？

邻接矩阵

即在二维数组中用0和1来表示两个结点之间邻接与否。结点需要映射到数组下标。

例子：

无向图的邻接矩阵

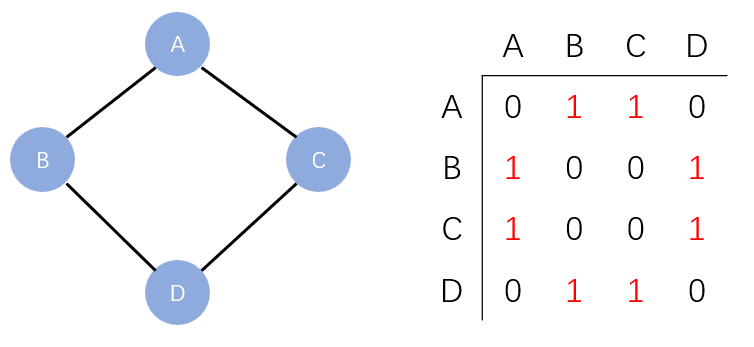
无向图的邻接矩阵是对称矩阵，所以可以进行压缩存储，将一个半角存到一个一维数组中，本文不细讲。

有向带权图的邻接矩阵：

矩阵中存权值，自己到自己（对角线）为0，非邻接点之间记为 $\infty$

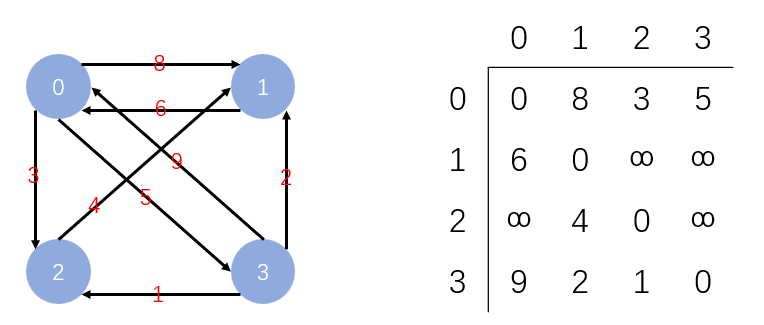
特点：

• 邻接矩阵适合存储稠密图
• 邻接矩阵可以以 $O(1)$ 的时间复杂度判断两个顶点之间的连接关系，并获得权值。
• 不适合查找一个顶点连接的所有边，时间复杂度为 $O(n)$

邻接表

使用数组表示顶点的集合，使用链表表示边的关系。

类似于我们在哈希表中讲的开散列。

例子：

图中 ABCD 分别标为 0123

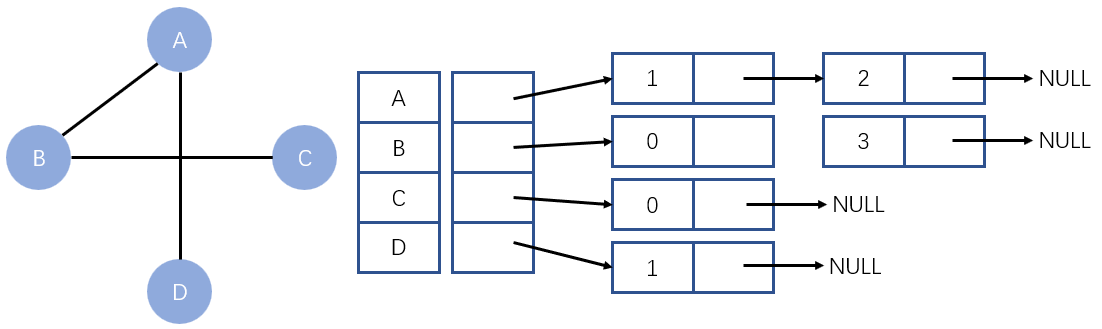
A 邻接 B 和 D，所以 A 后面挂两个结点；B 邻接 A C，所以 B 后面挂两个结点；C 邻接 B，所以 C 后面挂一个结点；D 邻接 A 所以 D 后面挂一个结点。

特点：

• 适合存储稀疏图
• 适合查找一个顶点连接出去的边
• 不适合确定两个顶点是否相连及权值

实现

图的创建一般有两种方式：

1. IO 输入，通过键盘或文件读取，不方便测试
2. 手动添加边

我们下面的实现采用第二种，方便我们调试。

邻接矩阵：

namespace matrix
{
	// V: 顶点, W: 权值, MAX_W: 默认∞为INT_MAX, Direction: 标志有向或无向,默认无向
	template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>
	class Graph
	{
	public:
		// 图的创建
		Graph(const V* a, size_t n)
		{
			// 开顶点数组
			_vertexs.reserve(n);
			// 把顶点插入数组，完成顶点与下标的映射（按插入顺序标号）
			for (size_t i = 0; i < n; ++i)
			{
				_vertexs.push_back(a[i]);
				_indexMap[a[i]] = i;
			}

			// 开矩阵，初始化为∞
			_matrix.resize(n);
			for (size_t i = 0; i < _matrix.size(); ++i)
			{
				_matrix[i].resize(n, MAX_W);
			}
		}

		// 获取顶点对应下标
		size_t GetVertexIndex(const V& v)
		{
			auto it = _indexMap.find(v);
			if (it != _indexMap.end())
			{
				return it->second;
			}
			else
			{
				throw invalid_argument("顶点不存在");
				return -1;
			}
		}

		// 添加边
		void AddEdge(const V& src, const V& dst, const W& w)
		{
			size_t srci = GetVertexIndex(src);
			size_t dsti = GetVertexIndex(dst);

			_matrix[srci][dsti] = w;

			// 如果是无向图，还要对称添加权值
			if (Direction == false)
			{
				_matrix[dsti][srci] = w;
			}

		}

		void Print()
		{
			// 顶点
			for (size_t i = 0; i < _vertexs.size(); ++i)
			{
				cout << "[" << i << "]" << "->" << _vertexs[i] << endl;
			}
			cout << endl;

			// 矩阵

			for (size_t i = 0; i < _matrix.size(); ++i)
			{
				for (size_t j = 0; j < _matrix[i].size(); ++j)
				{
					if (_matrix[i][j] == MAX_W)
					{
						cout << "*\t";
					}
					else
					{
						cout << _matrix[i][j] << "\t";
					}
				}
				cout << endl;
			}
		}

	private:
		vector<V> _vertexs;				 // 顶点集合
		unordered_map<V, int> _indexMap; // 顶点映射下标
		vector<vector<W>> _matrix;		 // 邻接矩阵
	};
}

测试：

void TestGraph1()
{
	matrix::Graph<char, int, INT_MAX, true> g("0123", 4);
	g.AddEdge('0', '1', 1);
	g.AddEdge('0', '3', 4);
	g.AddEdge('1', '3', 2);
	g.AddEdge('1', '2', 9);
	g.AddEdge('2', '3', 8);
	g.AddEdge('2', '1', 5);
	g.AddEdge('2', '0', 3);
	g.AddEdge('3', '2', 6);

	g.Print();
}

结果：

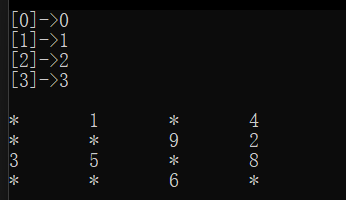
邻接表：

设计边的结构：

• 邻接表中，边首先需要一个指向后继的指针，边的权值，和边的一个起点或终点（对于有向图而言，如果存起点，则邻接表为入边表，如果存终点，则邻接表为出边表）。我们仅实现一个出边表。
• 邻接矩阵是二维数组，那么我们的邻接表要改为指针数组

namespace link_table
{
	template<class W>
	struct Edge
	{
		int _dsti; // 目标点下标
		W _w;	   // 权值
		Edge<W>* _next;

		Edge(int dsti, const W& w)
			: _dsti(dsti)
			, _w(w)
			, _next(nullptr)
		{}
	};

	// V: 顶点, W: 权值, Direction: 标志有向或无向,默认无向
	template<class V, class W, bool Direction = false>
	class Graph
	{
		typedef Edge<W> Edge;
	public:
		// 图的创建

		Graph(const V* a, size_t n)
		{
			// 开顶点数组
			_vertexs.reserve(n);
			// 把顶点插入数组，完成顶点与下标的映射（按插入顺序标号）
			for (size_t i = 0; i < n; ++i)
			{
				_vertexs.push_back(a[i]);
				_indexMap[a[i]] = i;
			}

			_tables.resize(n, nullptr);
		}

		// 获取顶点对应下标
		size_t GetVertexIndex(const V& v)
		{
			auto it = _indexMap.find(v);
			if (it != _indexMap.end())
			{
				return it->second;
			}
			else
			{
				throw invalid_argument("顶点不存在");
				return -1;
			}
		}

		// 添加边
		void AddEdge(const V& src, const V& dst, const W& w)
		{
			size_t srci = GetVertexIndex(src);
			size_t dsti = GetVertexIndex(dst);

			Edge* eg = new Edge(dsti, w);
			eg->_next = _tables[srci];
			_tables[srci] = eg;

			// 无向图还要对称添加边
			if (Direction == false)
			{
				Edge* eg = new Edge(srci, w);
				eg->_next = _tables[dsti];
				_tables[dsti] = eg;
			}
		}

		void Print()
		{
			for (size_t i = 0; i < _tables.size(); ++i)
			{
				cout << _vertexs[i] << "[" << i << "]->";
				Edge* cur = _tables[i];
				while (cur)
				{
					cout << _vertexs[cur->_dsti] << "[" << cur->_dsti << "]" << cur->_w << "->";
					cur = cur->_next;
				}
				cout << "nullptr" << endl;
			}
		}

	private:
		vector<V> _vertexs;				 // 顶点集合
		unordered_map<V, int> _indexMap; // 顶点映射下标
		vector<Edge*> _tables;			 // 邻接表
	};
}

测试：

void TestGraph2()
{
	string a[] = { "张三","李四","王五","赵六" };
	link_table::Graph<string, int, true> g(a, 4);
	g.AddEdge("张三", "李四", 100);
	g.AddEdge("张三", "王五", 200);
	g.AddEdge("王五", "赵六", 30);

	g.Print();
}

结果：

图的遍历

图的遍历针对的是顶点

广度优先遍历

从某一个顶点开始，一层一层往外遍历

和树的层序遍历类似，用队列来完成。访问队头顶点，然后让这个顶点的邻接点入队。与树不同的是，我们要额外注意以下几点：

如 A 访问过后 BCD 入队，B 访问过后 ACE 入队，这里有两个问题

1. A 已经访问过了，在访问 B 之后重复入队。所以我们需要一个数组来记录已经访问过的顶点
2. C 虽然没有被访问，但是访问 B 之后也重复入队了，所以我们还需要标记入队顶点

不难发现，访问过的顶点其实就是入队顶点的子集，所以这两个问题可以合并解决，即直接标记已经入队的顶点。

邻接矩阵版本BFS

void BFS(const V& src)
{
    size_t srci = GetVertexIndex(src);

    vector<bool> visited(_vertexs.size(), false);
    queue<int> q;

    q.push(srci);
    visited[srci] = true;

    size_t n = _vertexs.size();
    while (!q.empty())
    {
        int front = q.front();
        q.pop();
        cout << front << ":" << _vertexs[front] << endl;

        for (size_t i = 0; i < n; ++i)
        {
            if (_matrix[front][i] != MAX_W && !visited[i])
            {
                q.push(i);
                visited[i] = true;
            }
        }
    }
    cout << endl;
}

邻接表版本BFS：

void BFS(const V& src)
{
    size_t srci = GetVertexIndex(src);

    vector<bool> visited(_vertexs.size(), false);
    queue<int> q;

    q.push(srci);
    visited[srci] = true;

    while (!q.empty())
    {
        int front = q.front();
        q.pop();
        cout << front << ":" << _vertexs[front] << endl;

        Edge* cur = _tables[front];
        while (cur)
        {
            if (!visited[cur->_dsti])
            {
                q.push(cur->_dsti);
                visited[cur->_dsti] = true;
            }
            cur = cur->_next;
        }
    }
    cout << endl;
}

测试：

void TestBFS()
{
	string a[] = { "张三","李四","王五","赵六","孙七"};
	matrix::Graph<string, int> g(a, 5);
	g.AddEdge("张三", "李四", 100);
	g.AddEdge("张三", "王五", 200);
	g.AddEdge("王五", "赵六", 30);
	g.AddEdge("王五", "孙七", 30);

	g.Print();
	g.BFS("张三");
}

结果：

深度优先遍历

一条路走到底，走到无路可走了就回溯，重复这两步直到访问完全部顶点。

运用回溯算法，和访问标记数组，入队即标记，同上。

邻接矩阵版本DFS

void _DFS(size_t srci, vector<bool>& visited)
{
    cout << srci << ":" << _vertexs[srci] << endl;
    visited[srci] = true;

    for (size_t i = 0; i < _vertexs.size(); ++i)
    {
        if (_matrix[srci][i] != MAX_W && !visited[i])
        {
            _DFS(i, visited);
        }
    }
}

void DFS(const V& src)
{
    size_t srci = GetVertexIndex(src);
    vector<bool> visited(_vertexs.size(), false);

    _DFS(srci, visited);
}

邻接表版本DFS：

void _DFS(size_t srci, vector<bool>& visited)
{
    cout << srci << ":" << _vertexs[srci] << endl;
    visited[srci] = true;

    Edge* cur = _tables[srci];
    while (cur)
    {
        if (!visited[cur->_dsti])
        {
            _DFS(cur->_dsti, visited);
        }
        cur = cur->_next;
    }
}

void DFS(const V& src)
{
    size_t srci = GetVertexIndex(src);
    vector<bool> visited(_vertexs.size(), false);

    _DFS(srci, visited);
}

测试：

void TestDFS()
{
	string a[] = { "张三","李四","王五","赵六","孙七"};
	matrix::Graph<string, int> g(a, 5);
	g.AddEdge("张三", "李四", 100);
	g.AddEdge("张三", "王五", 200);
	g.AddEdge("王五", "赵六", 30);
	g.AddEdge("王五", "孙七", 30);

	g.Print();
	g.DFS("张三");
}

结果：

补充：

图的遍历常见操作就是寻找一个顶点连接出去的边，所以对于邻接表更合适一些。

另外上面我们只考虑了连通图，从一个顶点出发可以遍历完所有顶点，如果是非连通图呢？

解决方法：从 visited 数组中找没有遍历过的顶点再进行遍历

最小生成树

生成树：在无向图中，一个连通图的最小连通子图称为该图的生成树。有 $n$ 个顶点的连通图的生成树有 $n$ 个顶点和 $n-1$ 条边。

生成树不是唯一的。连通图的每一棵生成树，都是原图的一个极大无环子图，即：从中删去任何一条边，生成树就不再连通，反之，在其中引入任何一条新边，都会形成一条回路。

最小生成树：所有生成树中，边的权值之和最小的叫做最小生成树。

换句话说，最小生成树就是以最小的成本让这 $n$ 个顶点连通的树。

构造最小生成树的算法：Kruskal 算法和 Prim 算法。这两个算法都采用了贪心算法。

构造最小生成树的基本准则：

1. 尽可能使用图中权值最小的边来构造最小生成树
2. 只能使用恰好 $n-1$ 条边来连接图中 $n$ 个顶点
3. 选用的 $n-1$ 条边不能构成回路

Kruskal 算法

Kruskal 算法基本思想：按权值由小到大的顺序选择边。

首先将所有边按权值排序，或者用小堆来选权值最小的边。

为了避免选择的边形成环，我们把已选择的边所构成的各个连通子图看做各个集合，那么新选择的边的两个顶点应避免在同一个集合中。一条边选择完成后，将其两个顶点所在集合进行合并。

很明显，使用并查集可以方便地完成该算法。

算法可视化：

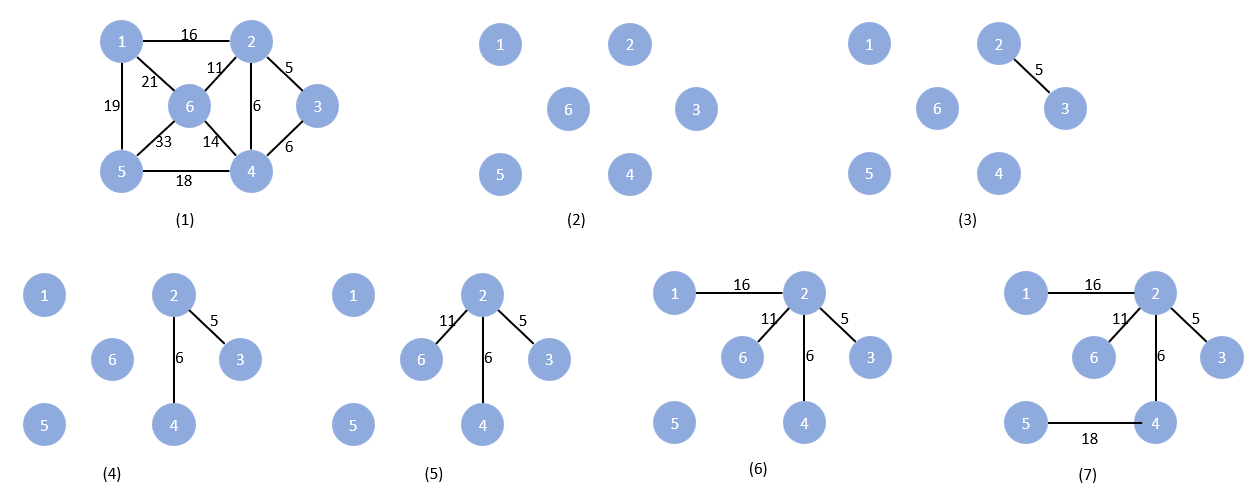
(3) 首先选择最小的边 5

(4) 然后从权值为 6 的两个边中任选一个

(5) 另一个权值为 6 的边不能选，因为选了就有环了。所以我们选权值为 11 的边

(6) 权值为 14 的边也不能选，只能选 16

(7) 选择剩余边中最小的，18，结束。

邻接矩阵：

• 因为邻接矩阵没有边的结构，所以我们专门写一个边的结构体。让它支持大于比较，以便于小堆的创建。
• 最小生成树通过输出型参数 Self& minTree 输出，返回值为最小生成树的边权和

// 设计边类，成员包含两个顶点和权值，并支持按权值比较
struct Edge
{
	size_t _srci;
	size_t _dsti;
	W _w;

	Edge(size_t srci, size_t dsti, const W& w)
		: _srci(srci)
		, _dsti(dsti)
		, _w(w)
	{}

	bool operator>(const Edge& e) const
	{
		return _w > e._w;
	}
};

W Kruskal(Self& minTree)
{
	size_t n = _vertexs.size();

	// 初始化最小生成树，顶点数组与映射关系与原图相同，邻接矩阵初始化为MAX_W
	minTree._vertexs = _vertexs;
	minTree._indexMap = _indexMap;
	minTree._matrix.resize(n);
	for (size_t i = 0; i < n; ++i)
	{
		minTree._matrix[i].resize(n, MAX_W);
	}

	// 创建小堆，并将所有边放进堆中
	priority_queue<Edge, vector<Edge>, greater<Edge>> minque;
	for (size_t i = 0; i < n; ++i)
	{
		for (size_t j = i; j < n; ++j)
		{
			if (_matrix[i][j] != MAX_W)
			{
				minque.emplace(i, j, _matrix[i][j]);
			}
		}
	}
			
	// 选出 n - 1 条边
	int size = 0;	// 记录已选边数
	W totalW = W();	// 记录最小生成树总权值
	UnionFindSet ufs(n);
	while (!minque.empty())
	{
		Edge min = minque.top();
		minque.pop();

		// 两点不在同一集合，则选择这条边，合并集合。
		if (!ufs.InSet(min._srci, min._dsti))
		{
			minTree._AddEdge(min._srci, min._dsti, min._w);
			ufs.Union(min._srci, min._dsti);
			++size;
			totalW += min._w;
		}
	}

	if (size == n - 1) return totalW;
	return W();
}

一些小动作：

包含自己的并查集：

#include "UnionFindSet.h"

在类的前面将自己的类型typedef一下：

typedef Graph<V, W, MAX_W, Direction> Self;

为了适应直接传入下标的情况，我们将添加边的函数拆成两份：

// 添加边
void AddEdge(const V& src, const V& dst, const W& w)
{
    size_t srci = GetVertexIndex(src);
    size_t dsti = GetVertexIndex(dst);

    _AddEdge(srci, dsti, w);
}

void _AddEdge(size_t srci, size_t dsti, const W& w)
{
    _matrix[srci][dsti] = w;

    // 如果是无向图，还要对称添加权值
    if (Direction == false)
    {
        _matrix[dsti][srci] = w;
    }
}

测试：

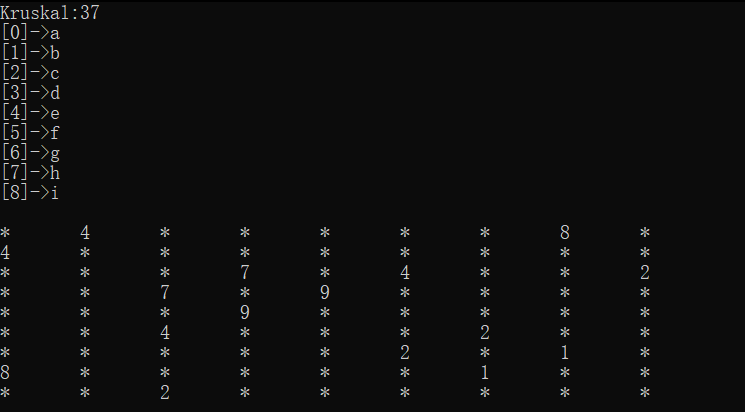
void TestGraphMinTree()
{
	const char* str = "abcdefghi";
	matrix::Graph<char, int> g(str, strlen(str));
	g.AddEdge('a', 'b', 4);
	g.AddEdge('a', 'h', 8);
	g.AddEdge('b', 'c', 8);
	g.AddEdge('b', 'h', 11);
	g.AddEdge('c', 'i', 2);
	g.AddEdge('c', 'f', 4);
	g.AddEdge('c', 'd', 7);
	g.AddEdge('d', 'f', 14);
	g.AddEdge('d', 'e', 9);
	g.AddEdge('e', 'f', 10);
	g.AddEdge('f', 'g', 2);
	g.AddEdge('g', 'h', 1);
	g.AddEdge('g', 'i', 6);
	g.AddEdge('h', 'i', 7);

	matrix::Graph<char, int> kminTree;
	cout << "Kruskal:" << g.Kruskal(kminTree) << endl;
	kminTree.Print();
}

结果：

邻接表：

邻接表的写法只要将原来的边结构稍微改一改，将边入堆的逻辑改一下，其余基本不变。

AddEdge 函数同样要拆开。

W Kruskal(Self& minTree)
{
    size_t n = _vertexs.size();

    // 初始化最小生成树，顶点数组与映射关系与原图相同，邻接表开空间
    minTree._vertexs = _vertexs;
    minTree._indexMap = _indexMap;
    minTree._tables.resize(n);

    // 创建小堆，并将所有边放进堆中
    priority_queue<Edge, vector<Edge>, greater<Edge>> minque;
    for (int i = 0; i < n; ++i)
    {
        Edge* cur = _tables[i];
        while (cur)
        {
            minque.emplace(i, cur->_dsti, cur->_w);
            cur = cur->_next;
        }
    }

    // 选出 n - 1 条边
    int size = 0;	// 记录已选边数
    W totalW = W();	// 记录最小生成树总权值
    UnionFindSet ufs(n);
    while (!minque.empty())
    {
        Edge min = minque.top();
        minque.pop();

        // 两点不在同一集合，则选择这条边，合并集合。
        if (!ufs.InSet(min._srci, min._dsti))
        {
            minTree._AddEdge(min._srci, min._dsti, min._w);
            ufs.Union(min._srci, min._dsti);
            ++size;
            totalW += min._w;
        }
    }

    if (size == n - 1) return totalW;
    return W();
}

修改后的边的结构：

template<class W>
struct Edge
{
	size_t _srci;
	size_t _dsti; // 目标点下标
	W _w;	   // 权值
	Edge<W>* _next;

	Edge(size_t srci, size_t dsti, const W& w)
		: _srci(srci)
		, _dsti(dsti)
		, _w(w)
		, _next(nullptr)
	{}

	Edge(size_t dsti, const W& w)
		: _srci(0)
		, _dsti(dsti)
		, _w(w)
		, _next(nullptr)
	{}

	bool operator>(const Edge& e) const
	{
		return _w > e._w;
	}
};

测试：

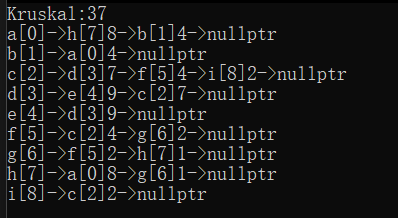
void TestGraphMinTree()
{
	const char* str = "abcdefghi";
	link_table::Graph<char, int> g(str, strlen(str));
	g.AddEdge('a', 'b', 4);
	g.AddEdge('a', 'h', 8);
	g.AddEdge('b', 'c', 8);
	g.AddEdge('b', 'h', 11);
	g.AddEdge('c', 'i', 2);
	g.AddEdge('c', 'f', 4);
	g.AddEdge('c', 'd', 7);
	g.AddEdge('d', 'f', 14);
	g.AddEdge('d', 'e', 9);
	g.AddEdge('e', 'f', 10);
	g.AddEdge('f', 'g', 2);
	g.AddEdge('g', 'h', 1);
	g.AddEdge('g', 'i', 6);
	g.AddEdge('h', 'i', 7);

	link_table::Graph<char, int> kminTree;
	cout << "Kruskal:" << g.Kruskal(kminTree) << endl;
	kminTree.Print();
}

结果：

Prim 算法

也是贪心算法，但是和 Kruskal 算法不同的是，Kruskal 算法是从全局，也就是所有剩余边中选。

而 Prim 算法是从给定的顶点开始往外选边最小的边

1. 我们将初始顶点放到一个集合 X 中，其余的顶点放到另一个集合 Y 中。
2. 在连接这两个集合的所有边中，选一条权值最小的。然后将这条边依附的集合 Y 的顶点转移到 X 中。
3. 重复第2步，直到所有顶点进入 X，所有选择的边构成的图即为最小生成树。

算法可视化：

从 1 开始构造最小生成树

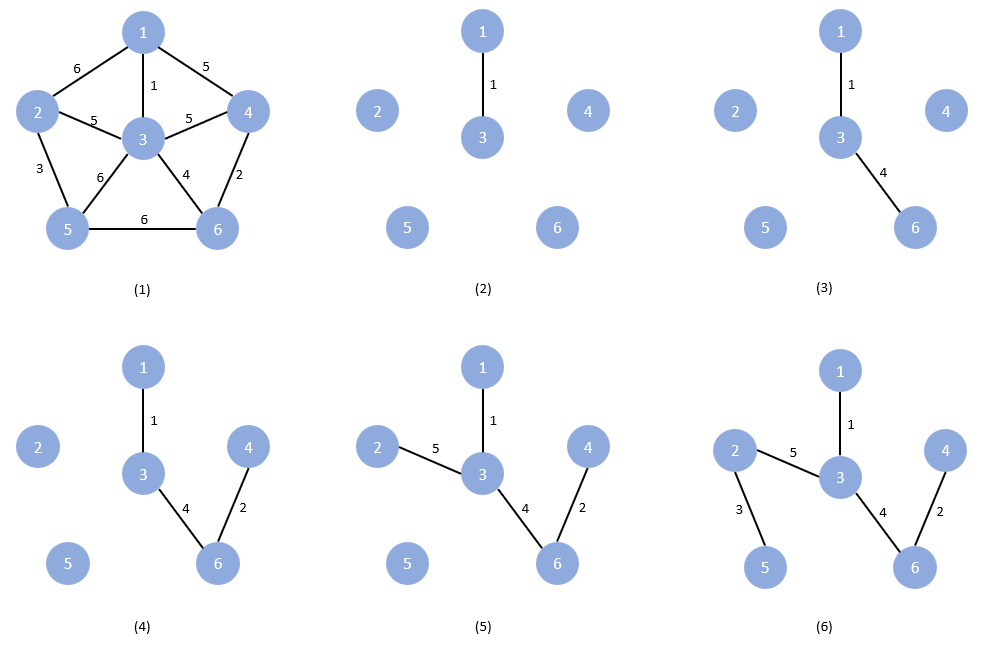
(2) 与 1 相关联的最小边权为1，我们选择这条边，并这条边的另一个顶点 3 移到集合 X 中

(3) 与 1、3 相关联的边中，权值最小的是4，选择这条边，并将顶点 6 移动 X 中

(4) 与 1、3、6 相关联的边中，最小的是 2，选择，并将 4 移到 X 中

(5) 与 1、3、6、4 相关联的边中，最小的权值是 5，但是与顶点 4 关联的那两条边所依附的顶点都在 X 中。所以只能选与 3 关联的边，将 2 移到 X 中。

(6) 与 1、3、6、4、2 相关联的边中，最小的权值是 3，选择这条边，将 5 移到 X 中。结束。

邻接矩阵：

• 重点在于选边的算法，如果暴力求最小边，时间复杂度为 $O(n^2)$ 。
• 所以我们使用堆，把每次新加入X的顶点所关联的边入堆，注意排除两个顶点都依附于 X 集合的边，这样可以避免重复入堆。
• 另外注意在选边的时候，依然要判断是否形成回路，因为只有两个集合，所以判断也很容易。
• 因为顶点不是在X集合就是在Y集合，所以可以不创建 Y 集合。

W Prim(Self& minTree, const V& src)
{
    size_t srci = GetVertexIndex(src);
    size_t n = _vertexs.size();

    // 初始化最小生成树，顶点数组与映射关系与原图相同，邻接矩阵初始化为MAX_W
    minTree._vertexs = _vertexs;
    minTree._indexMap = _indexMap;
    minTree._matrix.resize(n);
    for (size_t i = 0; i < n; ++i)
    {
        minTree._matrix[i].resize(n, MAX_W);
    }

    // 初始化集合
    unordered_set<size_t> X;
    X.insert(srci);

    // 选边
    // 先把 srci 连接的边添加到小堆中
    priority_queue<Edge, vector<Edge>, greater<Edge>> minq;
    for (size_t i = 0; i < n; ++i)
    {
        if (_matrix[srci][i] != MAX_W)
        {
            minq.emplace(srci, i, _matrix[srci][i]);
        }
    }

    size_t size = 0;
    W totalw = W();
    while (!minq.empty())
    {
        // 选一条最小的边
        Edge min = minq.top();
        minq.pop();
        // 判断是否构成环
        if (X.count(min._dsti)) continue;

        minTree._AddEdge(min._srci, min._dsti, min._w);
        ++size;
        totalw += min._w;
        if (size == n - 1)
            break;
        // 移动顶点
        X.insert(min._dsti);

        // 以刚进入X的顶点为起点，向小堆中添加新边，必须保证新边的另一个顶点在集合Y中
        for (size_t i = 0; i < n; ++i)
        {
            if (_matrix[min._dsti][i] != MAX_W && !X.count(i))
            {
                minq.emplace(min._dsti, i, _matrix[min._dsti][i]);
            }
        }
    }

    if (size == n - 1) return totalw;
    return W();
}

测试：

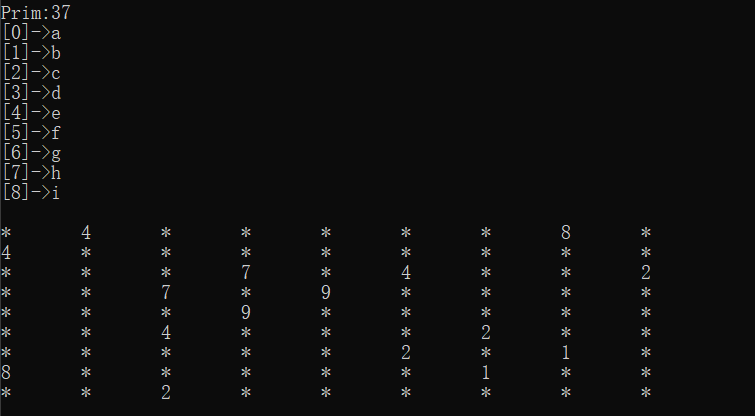
void TestGraphMinTreeM()
{
	const char* str = "abcdefghi";
	matrix::Graph<char, int> g(str, strlen(str));
	g.AddEdge('a', 'b', 4);
	g.AddEdge('a', 'h', 8);
	g.AddEdge('b', 'c', 8);
	g.AddEdge('b', 'h', 11);
	g.AddEdge('c', 'i', 2);
	g.AddEdge('c', 'f', 4);
	g.AddEdge('c', 'd', 7);
	g.AddEdge('d', 'f', 14);
	g.AddEdge('d', 'e', 9);
	g.AddEdge('e', 'f', 10);
	g.AddEdge('f', 'g', 2);
	g.AddEdge('g', 'h', 1);
	g.AddEdge('g', 'i', 6);
	g.AddEdge('h', 'i', 7);

	matrix::Graph<char, int> kminTree;
	cout << "Kruskal:" << g.Kruskal(kminTree) << endl;
	kminTree.Print();

	matrix::Graph<char, int> pminTree;
	cout << "Prim:" << g.Prim(pminTree, 'a') << endl;
	pminTree.Print();
}

结果：

邻接表：

W Prim(Self& minTree, const V& src)
{
    size_t srci = GetVertexIndex(src);
    size_t n = _vertexs.size();

    // 初始化最小生成树，顶点数组与映射关系与原图相同，邻接表开空间
    minTree._vertexs = _vertexs;
    minTree._indexMap = _indexMap;
    minTree._tables.resize(n);

    // 初始化集合
    unordered_set<size_t> X;
    X.insert(srci);

    // 选边
    // 先把 srci 连接的边添加到小堆中
    priority_queue<Edge, vector<Edge>, greater<Edge>> minq;
    Edge* cur = _tables[srci];
    while (cur)
    {
        minq.emplace(srci, cur->_dsti, cur->_w);
        cur = cur->_next;
    }

    size_t size = 0;
    W totalw = W();
    while (!minq.empty())
    {
        // 选一条最小的边
        Edge min = minq.top();
        minq.pop();
        // 判断是否构成环
        if (X.count(min._dsti)) continue;

        minTree._AddEdge(min._srci, min._dsti, min._w);
        ++size;
        totalw += min._w;
        if (size == n - 1)
            break;
        // 移动顶点
        X.insert(min._dsti);

        // 以刚进入X的顶点为起点，向小堆中添加新边，必须保证新边的另一个顶点在集合Y中
        Edge* cur = _tables[min._dsti];
        while (cur)
        {
            if (!X.count(cur->_dsti))
            {
                minq.emplace(min._dsti, cur->_dsti, cur->_w);
            }
            cur = cur->_next;
        }
    }

    if (size == n - 1) return totalw;
    return W();
}

测试：

void TestGraphMinTreeL()
{
	const char* str = "abcdefghi";
	link_table::Graph<char, int> g(str, strlen(str));
	g.AddEdge('a', 'b', 4);
	g.AddEdge('a', 'h', 8);
	g.AddEdge('b', 'c', 8);
	g.AddEdge('b', 'h', 11);
	g.AddEdge('c', 'i', 2);
	g.AddEdge('c', 'f', 4);
	g.AddEdge('c', 'd', 7);
	g.AddEdge('d', 'f', 14);
	g.AddEdge('d', 'e', 9);
	g.AddEdge('e', 'f', 10);
	g.AddEdge('f', 'g', 2);
	g.AddEdge('g', 'h', 1);
	g.AddEdge('g', 'i', 6);
	g.AddEdge('h', 'i', 7);

	link_table::Graph<char, int> kminTree;
	cout << "Prim:" << g.Prim(kminTree, 'a') << endl;
	kminTree.Print();
}

结果：

最短路径

最短路径问题：从带权有向图 $G$ 中的某一顶点出发，找出一条通往另一顶点的最短路径，最短路径就是边权和最小的路径。

单源最短路径问题：给定一个图 $G=(V,E)$，求源顶点 $s\in V$ 到图中每个结点 $v\in V$ 的最短路径

多源最短路径问题：给定一个图，求图中每一个顶点到其他顶点的最短路径

Dijkstra 算法

Dijkstra 算法适合解决带权有向图上的单源最短路径问题。同时算法要求图中所有边的权重非负

Dijkstra 算法的基本思想：按路径长度递增的顺序，逐个产生各最短路径

算法步骤：

1. 针对一个带权有向图 $G$，首先将所有结点分为两组 $S$ 和 $Q$，$S$ 是已经确定最短路径的顶点的集合(初始化只有一个起点)，$Q$ 是其余未确定最短路径的顶点的集合。对每一个顶点 $v_i$，用 $dist[i]$ 表示当前起点到顶点 $v_i$ 的路径长度，假设起点为 $v_0$，则初始化 $dist[0]=0$，其余顶点如果从 $v_0$ 到 $v_i$ 有弧（$v_0$ 可以直达 $v_i$），则 $dist[i]$ 为这条弧的权值，否则 $dist[i]=\infty$.

2. 选择 $v_k$，使得 $dist[k]=\min (dist[i]|v_i\in Q)$，并将 $v_k$ 从 $Q$ 移到 $S$ 中。

   即从 $Q$ 中选择一个起点 $v_0$ 到该顶点当前代价最小的顶点 $v_k$。$v_k$ 即确定为下一条最短路径的终点。

   将 $v_k$ 从 $Q$ 移到 $S$ 中。

3. 对从 $v_k$ 出发的每一个相邻结点 $v_j$，判断 $dist[j]$ 与 $dist[k]+弧(v_k,v_j)的权值$ 谁小。如果后者小，则更新，令 $dist[j]=dist[k]+弧(v_k,v_j)的权值$ 。这种操作叫作 松弛操作。

4. 重复 2、3 两步直到集合 $Q$ 为空。

证明：

我们可以证明，按长度递增的顺序来产生各个最短路径时，下一条最短路径要么是弧 $(v_0,v_x)$，要么是中间经过 $S$ 的某些顶点后到达 $v_x$ 的路径。中间不可能经过 $Q$ 中的顶点。

• 反证法：假设下一条最短路径上有一个顶点 $v_y$ 不在 $S$ 中，即此路径为 $(v_0,\cdots ,v_y,\cdots ,v_x)$。显然，$(v_0,\cdots ,v_y)$ 比 $(v_0,\cdots ,v_y,\cdots ,v_x)$ 更短，$v_y$ 才应该是下一条最短路径的终点，$(v_0,\cdots ,v_y)$ 才是下一条最短路径。这与假设矛盾，故假设不成立。

根据这个结果，我们可以得到，如果下一条最短路径终点为 $v_x$，那么，到 $v_x$ 的最短路径一定是弧 $(v_0,v_x)$ 的权值或者是 $dist[k](v_k\in S)$ 和弧 $(v_k,v_x)$ 的权值之和。

算法可视化：

以 s 为起点，橙色顶点表示已进入 S 集合的顶点，红色箭头表示已确定的最短路径。顶点内的值即为 $dist[]$

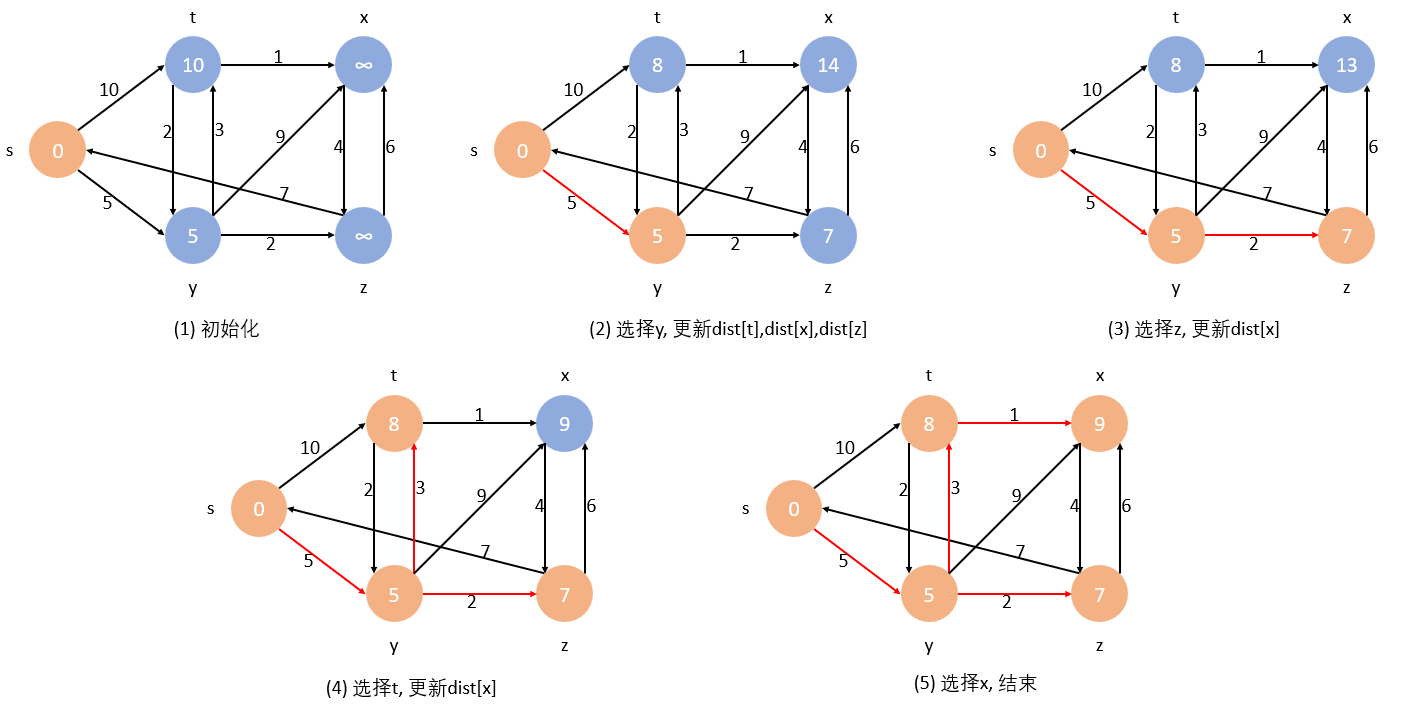
代码实现：

首先我们需要一个 $dist$ 数组用来存起点到每个顶点的最短路径长度，另外还需要一个 $parentPath(简称pPath)$ 数组存储路径前一个顶点的下标。

如上图，我们让 $syztx$ 分别映射到下标 $01234$

(1) 初始化后 p P a t h = { 0 , − 1 , − 1 , − 1 , − 1 } pPath=\{0,-1,-1,-1,-1\} pPath={0,−1,−1,−1,−1}，起点的父顶点设为它自己，其余顶点还未选出最短路径，父结点下标设为 -1

(2) p P a t h = { 0 , 0 , − 1 , − 1 , − 1 } pPath=\{0,0,-1,-1,-1\} pPath={0,0,−1,−1,−1}，确定 y 的父顶点是 s

(3) p P a t h = { 0 , 0 , 1 , − 1 , − 1 } pPath=\{0,0,1,-1,-1\} pPath={0,0,1,−1,−1}，确定 z 的父顶点是 y

(4) p P a t h = { 0 , 0 , 1 , 1 , − 1 } pPath=\{0,0,1,1,-1\} pPath={0,0,1,1,−1}，确定 t 的父顶点是 y

(5) p P a t h = { 0 , 0 , 1 , 1 , 3 } pPath=\{0,0,1,1,3\} pPath={0,0,1,1,3}，确定 x 的父顶点是 t，结束

写代码的时候，我们的初始化只是将起点的 $dist$ 设为 0，$pPath$ 设为它自己，其余的步骤在后面都可以合并。

当我们从 $Q$ 中找到下一个最短路径的终点的时候，我们并不能知道它的前一个顶点是谁，$pPath$ 也就无法直接写出来。但是在更新 $dist$ 的时候是知道的，所以我们可以让 $pPath$ 随着 $dist$ 的更新而更新。

邻接矩阵：

void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath)
{
    // 开空间+初始化
    size_t srci = GetVertexIndex(src);
    size_t n = _vertexs.size();
    dist.resize(n, MAX_W);
    pPath.resize(n, -1);
    dist[srci] = W();
    pPath[srci] = srci;

    unordered_set<size_t> S;
    for (size_t j = 0; j < n; ++j)
    {
        // 选出不在S中的当前代价最小的顶点u
        size_t u = 0;
        W min = MAX_W;
        for (size_t i = 0; i < n; ++i)
        {
            if (!S.count(i) && dist[i] < min)
            {
                u = i;
                min = dist[i];
            }
        }
        S.insert(u);

        // 更新从u顶点出发所到达的邻接点的dist和pPath
        for (size_t v = 0; v < n; ++v)
        {
            if (!S.count(v) && _matrix[u][v] != MAX_W && dist[u] + _matrix[u][v] < dist[v])
            {
                dist[v] = dist[u] + _matrix[u][v];
                pPath[v] = u;
            }
        }
    }
}

测试：

void TestDijkstra()
{
	const char* str = "syztx";
	size_t len = strlen(str);
	matrix::Graph<char, int, INT_MAX, true> g(str, len);
	g.AddEdge('s', 't', 10);
	g.AddEdge('s', 'y', 5);
	g.AddEdge('y', 't', 3);
	g.AddEdge('y', 'x', 9);
	g.AddEdge('y', 'z', 2);
	g.AddEdge('z', 's', 7);
	g.AddEdge('z', 'x', 6);
	g.AddEdge('t', 'y', 2);
	g.AddEdge('t', 'x', 1);
	g.AddEdge('x', 'z', 4);

	vector<int> dist;
	vector<int> pPath;
	g.Dijkstra('s', dist, pPath);
	for (size_t i = 0; i < len; ++i)
	{
		cout << dist[i] << ' ';
	}
	cout << endl;
	for (size_t i = 0; i < len; ++i)
	{
		cout << pPath[i] << ' ';
	}
}

结果：

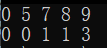
打印路径的函数：

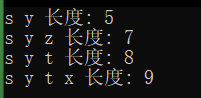
void PrintShortPath(const V& src, const vector<W>& dist, const vector<int>& pPath)
{
    size_t srci = GetVertexIndex(src);
    size_t n = _vertexs.size();
    for (size_t i = 0; i < n; ++i)
    {
        if (i != srci)
        {
            // 找出起点到i顶点的路径
            vector<int> path;
            size_t parenti = i;
            while (parenti != srci)
            {
                path.push_back(parenti);
                parenti = pPath[parenti];
            }
            reverse(path.begin(), path.end());
            cout << src << ' ';
            for (auto i : path)
            {
                cout << _vertexs[i] << " ";
            }
            cout << "长度: " << dist[i] << endl;
        }
    }
}

测试结果：

邻接表：

void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath)
{
    // 开空间+初始化
    size_t srci = GetVertexIndex(src);
    size_t n = _vertexs.size();
    dist.resize(n, MAX_W);
    pPath.resize(n, -1);
    dist[srci] = W();
    pPath[srci] = srci;

    unordered_set<size_t> S;
    for (size_t j = 0; j < n; ++j)
    {
        // 选出不在S中的当前代价最小的顶点u
        size_t u = 0;
        W min = MAX_W;
        for (size_t i = 0; i < n; ++i)
        {
            if (!S.count(i) && dist[i] < min)
            {
                u = i;
                min = dist[i];
            }
        }
        S.insert(u);

        // 更新从u顶点出发所到达的邻接点的dist和pPath
        Edge* cur = _tables[u];
        while (cur)
        {
            if (!S.count(cur->_dsti) && dist[u] + cur->_w < dist[cur->_dsti])
            {
                dist[cur->_dsti] = dist[u] + cur->_w;
                pPath[cur->_dsti] = u;
            }
            cur = cur->_next;
        }
    }
}

小动作：

因为 dist 数组涉及到了 $\infty$ ，所以从这里开始，邻接表也要加上一个非类型模板参数 W MAX_W = INT_MAX

template<class V, class W, bool Direction = false, W MAX_W = INT_MAX>

复杂度分析：

时间复杂度：选最小顶点和更新 $dist$ 的复杂度都是$O(n)$，外层又套了一层循环，所以整体的时间复杂度为 $O(n^2)$

空间复杂度：额外使用了两个数组和一个哈希表，空间复杂度为 $O(n)$

Bellman-Ford 算法

因为 Dijkstra 算法的基本原理是按路径长度递增的顺序，这意味着，每增加一条边我们都相信路径长度是递增的，那么每条边的权值都必须是正数，如果出现负数，Dijkstra 算法失效。

而 Bellman-Ford 算法可以解决负权图的单源最短路径问题，并且能够用来判断是否有负权回路。

当然它也有明显的缺点，哪就是它的时间复杂度为 $O(n\times e)$ ($n$ 是顶点数，$e$ 是边数)。普遍慢于 Dijkstra 算法。如果使用邻接矩阵来实现，那么因为遍历所有边的时间复杂度是 $O(n^2)$ 所以整体时间复杂度为 $O(n^3)$

从这里也可以看出，Bellman-Ford 算法实际上就是一种暴力求解更新。

---

我们先复习一下松弛操作：

对于边 $(u,v)$，令 $dist[v]=\min (dist[v],dist[u]+w(u,v))$

Bellman-Ford 算法的步骤就是不断尝试对每一条边进行松弛，每一轮循环对图上所有边进行一次松弛，我们将 $dist[v]$ 发生变化的松弛操作称为一次成功的松弛操作，当一轮循环中没有成功的松弛操作时，算法结束。

算法可视化：

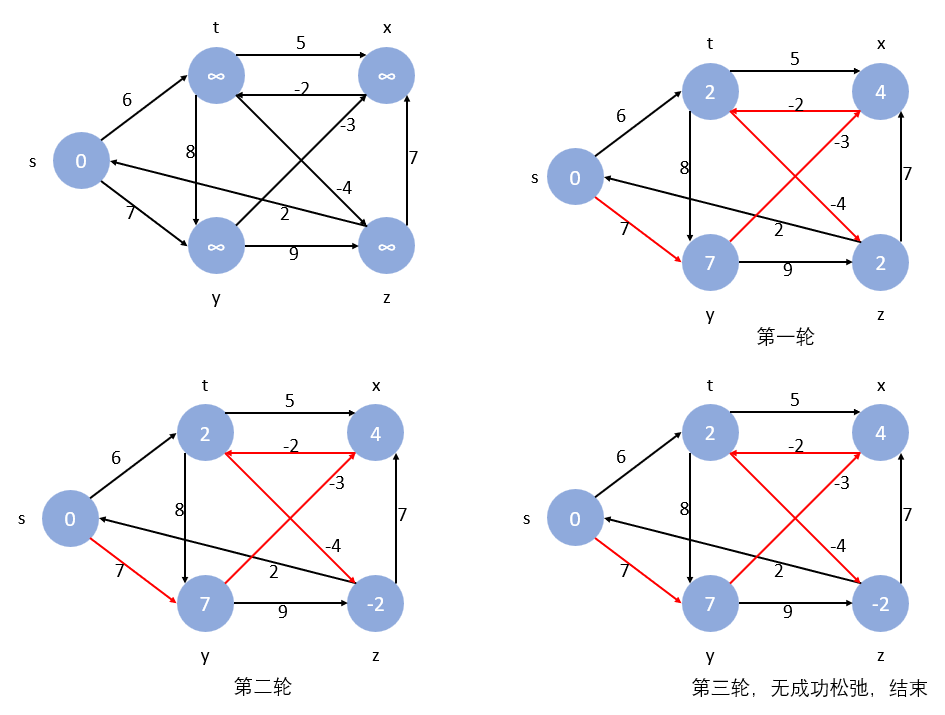
仔细观察细节可以发现第一轮松弛的最后，由于 $(x,t)$ 带的是负权，成功松弛，使得 $dist[t]$ 变得更小了，也就使得 $dist[t]+w(t,z)\ne dist[z]$ 需要进行下一轮松弛。直到第三轮发现没有可以松弛的边，算法结束。

在最短路存在的情况下，由于一轮松弛操作会使最短路的边数至少 $+1$，而最短路的边数为 $n-1$，因此整个算法最多执行 $n-1$ 轮松弛操作。

另外，如果从起点出发能抵达一个负环，则松弛操作会无休止地进行下去。因此如果第 $n$ 轮仍能进行成功的松弛操作，则说明从起点出发，能抵达一个负环。

带有负环的图无法求最短路径，因为在负环中可以越走越短无限循环。需要注意的是，从某一个起点出发，通过 Bellman-Ford 算法给出存在负环的结果，只能说明从该点出发能走到一个负环，如果没有给出存在负环的结果，不能说明整个图不存在负环。因此要判断整个图是否存在负环，需要从各个顶点出发分别使用 Bellman-Ford 算法，或者创建一个超级源点，让超级源点可以通过权值为 0 的弧直达其他所有顶点，然后从超级源点出发使用 Bellman-Ford 算法。

邻接矩阵：

bool BellmanFord(const V& src, vector<W>& dist, vector<int>& pPath)
{
    size_t n = _vertexs.size();
    size_t srci = GetVertexIndex(src);
    dist.resize(n, MAX_W);
    pPath.resize(n, -1);
    dist[srci] = W();
    pPath[srci] = srci;

    bool flag{};
    for (size_t k = 0; k < n; ++k)
    {
        flag = false;
        for (size_t i = 0; i < n; ++i)
        {
            for (size_t j = 0; j < n; ++j)
            {
                if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
                {
                    dist[j] = dist[i] + _matrix[i][j];
                    pPath[j] = i;
                    flag = true;
                }
            }
        }
        if (!flag) break;
    }
    return flag;
}

邻接表：

bool BellmanFord(const V& src, vector<W>& dist, vector<int>& pPath)
{
    size_t n = _vertexs.size();
    size_t srci = GetVertexIndex(src);
    dist.resize(n, MAX_W);
    pPath.resize(n, -1);
    dist[srci] = W();
    pPath[srci] = srci;

    bool flag{};
    for (size_t k = 0; k < n; ++k)
    {
        flag = false;
        for (size_t i = 0; i < n; ++i)
        {
            Edge* cur = _tables[i];
            while (cur)
            {
                if (dist[i] + cur->_w < dist[cur->_dsti])
                {
                    dist[cur->_dsti] = dist[i] + cur->_w;
                    pPath[cur->_dsti] = i;
                    flag = true;
                }
                cur = cur->_next;
            }
        }
        if (!flag) break;
    }
    return flag;
}

测试：

void TestBellmanFord()
{
	const char* str = "syztx";
	size_t len = strlen(str);
	matrix::Graph<char, int, INT_MAX, true> g(str, len);
	g.AddEdge('s', 'y', 7);
	g.AddEdge('s', 't', 6);
	g.AddEdge('y', 'z', 9);
	g.AddEdge('y', 'x', -3);
	g.AddEdge('z', 's', 2);
	g.AddEdge('z', 'x', 7);
	g.AddEdge('t', 'y', 8);
	g.AddEdge('t', 'z', -4);
	g.AddEdge('t', 'x', 5);
	//g.AddEdge('t', 'y', -1); // 添加此边构成负环
	g.AddEdge('x', 't', -2);

	vector<int> dist;
	vector<int> pPath;
	if (g.BellmanFord('s', dist, pPath)) cout << "有负权回路";
	else g.PrintShortPath('s', dist, pPath);
}

结果：

---

Bellman-Ford 算法的队列优化

该优化又称 SPFA(Shortest Path Faster Algorithm)，是对 Bellman-Ford 算法的一种优化算法。

显然在 Bellman-Ford 算法中有很多无用的松弛操作，实际上，只有上一次成功松弛的边，才有可能引起下一次的松弛操作。

我们可以用一个队列来维护可能引起松弛操作的结点。

算法步骤：

创建一个队列来保存待优化的结点，优化时每次取出队首结点 $u$，对 $u$ 点的出边 $(u,v)$ 进行松弛操作，如果松弛成功，且 $v$ 点不在当前的队列中，就将 $v$ 点放入队尾。这样不断从队列中取出结点来进行松弛操作，直至队列空为止。

如果一个顶点入队达到n次，说明有负环。

代码实现：

邻接矩阵：

bool spfa(const V& src, vector<W>& dist, vector<int>& pPath)
{
    size_t n = _vertexs.size();
    size_t srci = GetVertexIndex(src);
    dist.resize(n, MAX_W);
    pPath.resize(n, -1);
    dist[srci] = W();
    pPath[srci] = srci;

    queue<int> q;
    vector<int> cnt(n, 0); // 记录各点入队次数，用于判断负环
    vector<bool> flag(n, false); // 判断是否在队列中
    q.push(srci);
    ++cnt[srci];
    flag[srci] = true;

    while (!q.empty())
    {
        int u = q.front();
        q.pop();
        flag[u] = false;
        for (size_t v = 0; v < n; ++v)
        {
            if (_matrix[u][v] != MAX_W && dist[u] + _matrix[u][v] < dist[v])
            {
                dist[v] = dist[u] + _matrix[u][v];
                pPath[v] = u;
                if (!flag[v])
                {
                    q.push(v);
                    ++cnt[v];
                    flag[v] = true;
                    if (cnt[v] == n) return true;
                }
            }
        }
    }
    return false;
}

邻接表：

bool spfa(const V& src, vector<W>& dist, vector<int>& pPath)
{
    size_t n = _vertexs.size();
    size_t srci = GetVertexIndex(src);
    dist.resize(n, MAX_W);
    pPath.resize(n, -1);
    dist[srci] = W();
    pPath[srci] = srci;

    queue<int> q;
    vector<int> cnt(n, 0); // 记录各点入队次数，用于判断负环
    vector<bool> flag(n, false); // 判断是否在队列中
    q.push(srci);
    ++cnt[srci];
    flag[srci] = true;

    while (!q.empty())
    {
        int u = q.front();
        q.pop();
        flag[u] = false;

        Edge* cur = _tables[u];
        while (cur)
        {
            if (dist[u] + cur->_w < dist[cur->_dsti])
            {
                dist[cur->_dsti] = dist[u] + cur->_w;
                pPath[cur->_dsti] = u;
                if (!flag[cur->_dsti])
                {
                    q.push(cur->_dsti);
                    ++cnt[cur->_dsti];
                    flag[cur->_dsti] = true;
                    if (cnt[cur->_dsti] == n) return true;
                }
            }
            cur = cur->_next;
        }
    }
    return false;
}

SPFA算法还有四个优化策略：

• 堆优化：将队列换成堆，与 Dijkstra 的区别是允许一个点多次入堆。在有负权边的图可能被卡成指数级复杂度。
• 栈优化，在寻找负环时可能具有更高效率，但最坏时间复杂度仍然为指数级。
• SLF：Small Label First 策略，设要加入的节点是 $j$，队首元素为 $i$，若 $dist(j)<dist(i)$，则将 $j$ 插入队首，否则插入队尾；
• LLL：Large Label Last 策略，设队首元素为 $i$，队列中所有 $dist$ 值的平均值为 $x$，若 $dist(i)>x$ 则将 $i$ 插入到队尾，查找下一元素，直到找到某一 $i$ 使得 $dist(i)⩽x$，则将 $i$ 出队进行松弛操作。

SLF 和 LLL 优化在随机数据上表现优秀，但是在正权图上最坏情况为 $O(VE)$，在负权图上最坏情况为达到指数级复杂度

Floyd 算法

Dijkstra 算法和 Bellman-Ford 算法都是用来解决单源最短路径问题的。当然我们可以以每个顶点为源顶点，分别用一次 Dijkstra 算法或 Bellman-Ford 算法来解决多源最短路径问题，但是 Dijkstra 算法不支持负权图，Bellman-Ford 这样做太慢。

使用 Floyd 算法可以更高效地解决多源最短路径问题。

Floyd 算法采用动态规划的策略，也适用于带负权图。其时间复杂度为 $O(n^3)$

原理：

状态定义

设 $f(i,j,k)$ 为从 $i$ 到 $j$ 的只以 $(1\dots k)$ 集合中的顶点为中间顶点的最短路径长度。也就是说，只考虑在顶点 $1$ 到 $k$ 所构成的子图中从 $i$ 到 $j$ 的路径（大问题化小问题）。

状态分析与转移

假设已求得只以 $(1\dots k-1)$ 集合中的顶点为中间顶点时，各对顶点间的最短路长度，那么求 $(1\dots k)$ 状态时，可以发现，这一状态的考虑范围只是在前一个状态下增加了一个顶点 $k$，那么新的最短路径无非就是经过 $k$ 和不经过 $k$ 两种取其一。

1. 若最短路径经过点 $k$，即 $i$ 到 $j$ 等于 $i$ 到 $k$ 加 $k$ 到 $j$，则 $f(i,j,k)=f(i,k,k-1)+f(k,j,k-1)$
2. 若最短路径不经过点 $k$，即增加一个顶点 $k$ 没有影响，则 $f(i,j,k)=f(i,j,k-1)$

因此，$f(i,j,k)=\min (f(i,k,k-1)+f(k,j,k-1),f(i,j,k-1))$

初始化：

在 $k=0$ 时，即 $f(x,y,0)$ 为，若 $x$ 到 $y$ 有直接相连的边，则为该边权，若 $x$ 到 $y$ 无直接相连的边，则为$\infty$，若 $x=y$，则为 $0$.

最后：由于 $k$ 是由 $k-1$ 推过来的，所以第三维可以优化掉，注意遍历顺序从小到大即可。

代码实现：

我们的 dist 和 pPath 都要升到二维
dist[i][j] 表示从 i 到 j 的最短路径长度
pPath[i][j] 表示以 i 为源点的最短路径中 j 的父顶点

邻接矩阵

void Floyd(vector<vector<W>>& dist, vector<vector<int>>& pPath)
{
    // 开空间
    size_t n = _vertexs.size();
    dist.resize(n);
    pPath.resize(n);
    for (size_t i = 0; i < n; ++i)
    {
        dist[i].resize(n, MAX_W);
        pPath[i].resize(n, -1);
    }
    // 初始化
    for (size_t i = 0; i < n; ++i)
    {
        for (size_t j = 0; j < n; ++j)
        {
            if (_matrix[i][j] != MAX_W)
            {
                dist[i][j] = _matrix[i][j];
                pPath[i][j] = i;
            }
            if (i == j)
                dist[i][j] = W();
        }
    }
    // 最短路径的更新
    for (size_t k = 0; k < n; ++k)
    {
        for (size_t i = 0; i < n; ++i)
        {
            for (size_t j = 0; j < n; ++j)
            {
                if (dist[i][k] != MAX_W && dist[k][j] != MAX_W && dist[i][k] + dist[k][j] < dist[i][j])
                {
                    dist[i][j] = dist[i][k] + dist[k][j];
                    pPath[i][j] = pPath[k][j];
                }
            }
        }
    }
}

注意：应特别注意 $pPath$ 的更新，若最短路径经过$k$，那么 $j$ 的父顶点不一定是 $k$，而是在以 $k$ 为源点时 $j$ 的父顶点。

测试：

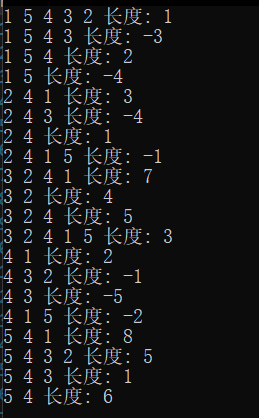
void TestFloyd()
{
	const char* str = "12345";
	size_t len = strlen(str);
	matrix::Graph<char, int, INT_MAX, true> g(str, len);
	g.AddEdge('1', '2', 3);
	g.AddEdge('1', '3', 8);
	g.AddEdge('1', '5', -4);
	g.AddEdge('2', '4', 1);
	g.AddEdge('2', '5', 7);
	g.AddEdge('3', '2', 4);
	g.AddEdge('4', '1', 2);
	g.AddEdge('4', '3', -5);
	g.AddEdge('5', '4', 6);

	vector<vector<int>> dist;
	vector<vector<int>> pPath;
	g.Floyd(dist, pPath);

	for (size_t i = 0; i < len; ++i)
	{
		g.PrintShortPath(str[i], dist[i], pPath[i]);
	}
}

结果：

邻接表：

void Floyd(vector<vector<W>>& dist, vector<vector<int>>& pPath)
{
    // 开空间
    size_t n = _vertexs.size();
    dist.resize(n);
    pPath.resize(n);
    for (size_t i = 0; i < n; ++i)
    {
        dist[i].resize(n, MAX_W);
        pPath[i].resize(n, -1);
    }
    // 初始化
    for (size_t i = 0; i < n; ++i)
    {
        Edge* cur = _tables[i];
        while (cur)
        {
            dist[i][cur->_dsti] = cur->_w;
            pPath[i][cur->_dsti] = i;
            cur = cur->_next;
        }
        dist[i][i] = W();
    }

    // 最短路径的更新
    for (size_t k = 0; k < n; ++k)
    {
        for (size_t i = 0; i < n; ++i)
        {
            for (size_t j = 0; j < n; ++j)
            {
                if (dist[i][k] != MAX_W && dist[k][j] != MAX_W && dist[i][k] + dist[k][j] < dist[i][j])
                {
                    dist[i][j] = dist[i][k] + dist[k][j];
                    pPath[i][j] = pPath[k][j];
                }
            }
        }
    }
}