7-1 入度与出度
分数 10
全屏浏览
切换布局
作者 黄龙军
单位 绍兴文理学院
求有向图G中各顶点的入度与出度。建议分别采用邻接矩阵和邻接表这两种不同的存储结构完成。
输入格式:
首先输入一个正整数T,表示测试数据的组数,然后是T组测试数据。每组测试第一行输入2个整数n、m(2≤n≤26,1≤m≤n(n-1)/2),分别表示顶点数、边数;然后输入m行,每行包含两个顶点Ai、Bi(大写字母表示),表示Ai到Bi有一条有向边。
输出格式:
对于每组测试,输出n行,依顶点的字典序在每行上输出各顶点的入度和出度(数据之间留一个空格)。
输入样例:
1
5 4
A C
A B
B D
E C
输出样例:
0 2
1 1
2 0
1 0
0 1#include <iostream>
#include <cstring>
using namespace std;
const int N=36;
int t,n,m;
int r[N],c[N];
int h[N],e[N],ne[N],idx;
void add(int a,int b)
{
e[idx]=b;ne[idx]=h[a];h[a]=idx++;
}
int main()
{
cin>>t;
while(t--)
{memset(h,-1,sizeof(h));
idx=0;
memset(r,0,sizeof(r));
memset(c,0,sizeof(c));
cin>>n>>m;
for(int i=0;i<m;i++)
{
char a,b;
cin>>a>>b;
// cout<<a<<" "<<b<<endl;
int u=a-'A'+1,v=b-'A'+1;
add(u,v);
c[u]++,r[v]++;
}
for(int i=1;i<=n;i++)
cout<<r[i]<<" "<<c[i]<<endl;
}
}7-2 图的存储-邻接表
分数 15
全屏浏览
切换布局
作者 唐艳琴
单位 中国人民解放军陆军工程大学
输出给定图的邻接表。
输入格式:
输入第一行给出三个正整数,分别表示无向图的节点数N(1<N≤10)、边数M(≤50)和有向或无向标志S(1表示有向图,0表示无向图)。
随后的M行对应M条边,每行给出一对正整数,分别是该条边直接连通的两个节点的编号(编号范围1~N)。
输出格式:
输出图的邻接表,从第0行开始按顺序输出,共输出N行,具体样式见输出样例。冒号前后无空格,每个元素间有一个空格,末尾均有一空格。
由于图的存储是不唯一的,为了使得输出具有唯一的结果,我们约定以表头插入法构造邻接表。
输入样例:
6 8 0
1 2
2 3
3 4
4 5
5 6
6 4
3 6
1 5
输出样例:
0:4 1
1:2 0
2:5 3 1
3:5 4 2
4:0 5 3
5:2 3 4 #include <iostream>
#include <cstring>
using namespace std;
const int N=20,M=60;
int s,n,m;
int h[N],e[N],ne[N],idx;
void add(int a,int b)
{
e[idx]=b;ne[idx]=h[a];h[a]=idx++;
}
int main()
{
memset(h,-1,sizeof(h));
cin>>n>>m>>s;
while(m--)
{
int x,y;
cin>>x>>y;
add(x-1,y-1);
if(!s) add(y-1,x-1);
}
for(int i=0;i<n;i++)
{
cout<<i<<":";
for(int j=h[i];j!=-1;j=ne[j])
{
int k=e[j];
cout<<k<<" ";
}
cout<<endl;
}
}
7-3 满树的遍历
分数 15
全屏浏览
切换布局
作者 陈越
单位 浙江大学
一棵“k 阶满树”是指树中所有非叶结点的度都是 k 的树。给定一棵树,你需要判断其是否为 k 阶满树,并输出其前序遍历序列。
注:树中结点的度是其拥有的子树的个数,而树的度是树内各结点的度的最大值。
输入格式:
输入首先在第一行给出一个正整数 n(≤105),是树中结点的个数。于是设所有结点从 1 到 n 编号。
随后 n 行,第 i 行(1≤i≤n)给出第 i 个结点的父结点编号。根结点没有父结点,则对应的父结点编号为 0。题目保证给出的是一棵合法多叉树,只有唯一根结点。
输出格式:
首先在一行中输出该树的度。如果输入的树是 k 阶满树,则加 1 个空格后输出 yes,否则输出 no。最后在第二行输出该树的前序遍历序列,数字间以 1 个空格分隔,行首尾不得有多余空格。
注意:兄弟结点按编号升序访问。
输入样例 1:
7
6
5
5
6
6
0
5
输出样例 1:
3 yes
6 1 4 5 2 3 7
输入样例 2:
7
6
5
5
6
6
0
4
输出样例 2:
3 no
6 1 4 7 5 2 3#include <iostream>
#include <vector>
using namespace std;
const int N=1e5+10;
vector<int>list[N];
int cd[N];
int rt;
void dfs(int x)
{
if(x!=rt) cout<<" ";
cout<<x;
for(int i=0;i<list[x].size();i++)
{
dfs(list[x][i]);
}
}
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
int fa;
cin>>fa;
list[fa].push_back(i);
cd[fa]++;
if(!fa) rt=i;
}
int key=0,Max=0;
for(int i=1;i<=n;i++)
{
if(cd[i]==0) continue;
if(Max==0) Max=cd[i];
else if(cd[i]!=Max)
{
key=1;
Max=max(Max,cd[i]);
}
}
if(key) cout<<Max<<" "<<"no"<<endl;
else cout<<Max<<" "<<"yes"<<endl;
dfs(rt);
}7-4 有向图的拓扑序列
分数 20
输出有向图的拓扑序列。
输入格式:
输入第一行给出两个正整数,分别表示图的节点数N(1<N≤10)、边数M(≤50)。随后的M行对应M条边,每行给出一对正整数,分别是有向边直接连通的两个节点的编号(编号从1到N依次进行)。
输出格式:
输出此图的拓扑序列,用一个空格隔开,最后也有一个空格;如果为非连通图或图中有回路,则在结尾处另起一行输出一个0。
由于拓扑序列是不唯一的,为了使得输出具有唯一的结果,我们约定以表头插入法构造邻接表,并且保证初始入度为0的节点仅有一个。当运行过程中同时出现多个入度为0 的结点时,采用栈来保存。
输入样例1:
4 3
1 4
4 2
2 3
输出样例1:
1 4 2 3
输入样例2:
4 4
1 4
4 2
2 3
3 4
输出样例2:
1
0#include <iostream>
#include <cstring>
#include <stack>
using namespace std;
const int N=20,M=60;
int n,m;
int h[N],e[N],ne[N],idx;
int r[N];
bool st[N];
int res[N],k=0;
void add(int a,int b)
{
e[idx]=b;ne[idx]=h[a];h[a]=idx++;
}
void topsort()
{
stack<int>stk;
for(int i=1;i<=n;i++)
{
if(r[i]==0)
{
stk.push(i);
}
}
while(!stk.empty())
{
int t=stk.top();
cout<<t<<" ";
k++;
stk.pop();
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
r[j]--;
if(r[j]==0)
{
stk.push(j);
}
}
}
if(k<n) cout<<endl<<0;
}
int main()
{
cin>>n>>m;
memset(h,-1,sizeof(h));
while(m--)
{
int x,y;
cin>>x>>y;
add(x,y);
r[y]++;
}
topsort();
}7-5 【模板】Floyd
分数 20
全屏浏览
切换布局
作者 苏国煜
单位 闽江学院
给出一张由 n 个点 m 条边组成的无向图。
求出所有点对 (i,j) 之间的最短路径。
输入格式:
第一行为两个整数 n,m,分别代表点的个数和边的条数。
接下来 m 行,每行三个整数 u,v,w,代表 u,v 之间存在一条边权为 w 的边。
输出格式:
输出 n 行每行 n 个整数。
第 i 行的第 j 个整数代表从 i 到 j 的最短路径。
输入样例:
在这里给出一组输入。例如:
4 4
1 2 1
2 3 1
3 4 1
4 1 1
输出样例:
在这里给出相应的输出。例如:
0 1 2 1
1 0 1 2
2 1 0 1
1 2 1 0#include <iostream>
#include <cstring>
using namespace std;
const int N=110,M=4510,W=1010,INF=0x3f3f3f3f;
int d[N][N];
int n,m,w;
void floyd()
{
for(int k=1;k<=n;k++)
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
}
}
}
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(i==j) d[i][j]=0;
else d[i][j]=INF;
}
}
while(m--)
{
int x,y,w;
cin>>x>>y>>w;
d[x][y]=d[y][x]=min(d[x][y],w);
// cout<<d[x][y]<<endl;
}
floyd();
for(int i=1;i<=n;i++)
{
int flag=1;
for(int j=1;j<=n;j++)
{
if(!flag) cout<<" ";
flag=0;
cout<<d[i][j];
}
if(i!=n)
cout<<endl;
}
}7-6 Dijkstra算法(模板)
分数 20
全屏浏览
切换布局
作者 李廷元
单位 中国民用航空飞行学院
给一个n(1 ≤ n ≤ 2500) 个点 m(1 ≤ m ≤ 6200) 条边的无向图,求 s 到 t 的最短路。
输入格式:
第一行四个由空格隔开的整数 n、m、s、t。
之后的 m 行,每行三个正整数 si、ti、wi(1≤wi≤109),表示一条从si 到 ti 长度为 wi 的边。
输出格式:
一个整数,表示从s 到t 的最短路径长度。数据保证至少存在一条道路。
输入样例:
7 11 5 4
2 4 2
1 4 3
7 2 2
3 4 3
5 7 5
7 3 3
6 1 1
6 3 4
2 4 3
5 6 3
7 2 1
输出样例:
7#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N=2510,M=6210;
int n,m,s,t;
int h[N],e[2*N],w[2*M],ne[2*M],idx;
int dist[N];
bool st[N];
void add(int a,int b,int c)
{
e[idx]=b;w[idx]=c;ne[idx]=h[a];h[a]=idx++;
}
void spfa()
{
queue<int>q;
memset(dist,0x3f,sizeof(dist));
dist[s]=0;
q.push(s);
st[s]=true;
while(!q.empty())
{
int k=q.front();
// cout<<k<<endl;
q.pop();
st[k]=false;
for(int i=h[k];i!=-1;i=ne[i])
{
int j=e[i];
if(dist[j]>dist[k]+w[i])
{
dist[j]=dist[k]+w[i];
if(!st[j])
{
q.push(j);
st[j]=true;
}
}
}
}
cout<< dist[t];
}
int main()
{
memset(h,-1,sizeof(h));
cin>>n>>m>>s>>t;
while(m--)
{
int x,y,z;
cin>>x>>y>>z;
add(x,y,z);
add(y,x,z);
}
spfa();
}
7-7 最小生成树-kruskal
分数 10
全屏浏览
切换布局
作者 任唯
单位 河北农业大学
题目给出一个无向连通图,要求求出其最小生成树的权值。
温馨提示:本题请使用kruskal最小生成树算法。
输入格式:
第一行包含两个整数 N(1<=N<=1x106),M(1<=M<=1x106) 表示该图共有 N 个结点和 M 条无向边。
接下来 M 行每行包含三个整数 Xi,Yi,Zi ,表示有一条长度为 Zi 的无向边连接结点 Xi,Yi 。
输出格式:
输出一个整数表示最小生成树的各边的长度之和。
输入样例:
4 5
1 2 2
1 3 2
1 4 3
2 3 4
3 4 3
输出样例:
7#include <iostream>
#include <algorithm>
using namespace std;
const int N=1e6+10;
int n,m;
int p[N];
int cnt;
struct Edge
{
int a,b,w;
bool operator <(const Edge &t)
{
return w<t.w;
}
}edges[N];
int find(int x)
{
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
}
void kuskal()
{
for(int i=1;i<=n;i++) p[i]=i;
sort(edges,edges+m);
int res=0;
for(int i=0;i<m;i++)
{
int a=edges[i].a,b=edges[i].b,w=edges[i].w;
if(find(a)!=find(b))
{
p[find(a)]=find(b);
res+=w;
}
}
cout<<res;
}
int main()
{
cin>>n>>m;
for(int i=0;i<m;i++)
{
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
edges[i].a=x,edges[i].b=y,edges[i].w=z;
}
kuskal();
}
7-8 最小生成树构造-prim算法
分数 15
全屏浏览
切换布局
作者 唐艳琴
单位 中国人民解放军陆军工程大学
某地对偏远地区实行“村村通”工程,目标是使整个地区任何两个村落间都可以实现快速交通(但不一定有直接的快速道路相连,只要互相间接通过快速路可达即可)。现得到拟修建道路的费用,现请你编写程序,计算出需修建哪几条道路,能够保证全地区畅通并且造价最低。
输入格式:
输入的第一行给出村庄数目N (1≤N≤20)和拟修建的道路数M
接下来的M行对应修建每条村庄间道路的成本,每行给出3个正整数,分别是两个村庄的编号(从1编号到N),此两村庄间道路的成本。
输出格式:
输出需修建的道路,按prim算法从编号1开始得到的顺序,输出每条路,每行输出一条道路,形式如:道路1编号,道路2编号,费用。(编号小的放前面,编号大的放后面,逗号为英文状态下的逗号)
输入样例:
4 6
1 2 1
1 3 4
1 4 1
2 3 3
2 4 2
3 4 5
输出样例:
1,2,1
1,4,1
2,3,3#include <iostream>
#include <cstring>
using namespace std;
const int N=30;
int n,m;
int g[N][N];
int dist[N];
bool st[N];
int pre[N];
void prim()
{
memset(dist,0x3f,sizeof(dist));
int res=0;
for(int i=0;i<n;i++)
{
int t=-1;
for(int j=1;j<=n;j++)
{
if(!st[j]&&(t==-1||dist[j]<dist[t]))
t=j;
}
st[t]=true;
if(i)
{
if(pre[t]<t)
cout<<pre[t]<<","<<t<<","<<dist[t]<<endl;
else
cout<<t<<","<<pre[t]<<","<<dist[t]<<endl;
}
for(int j=1;j<=n;j++)
if(dist[j]>g[t][j])
{
dist[j]=g[t][j];
pre[j]=t;
}
}
}
int main()
{
cin>>n>>m;
memset(g,0x3f,sizeof(g));
while(m--)
{
int x,y,w;
cin>>x>>y>>w;
g[x][y]=g[y][x]=min(g[x][y],w);
}
prim();
}7-9 浪漫侧影
分数 25
全屏浏览
切换布局
作者 陈越
单位 浙江大学

“侧影”就是从左侧或者右侧去观察物体所看到的内容。例如上图中男生的侧影是从他右侧看过去的样子,叫“右视图”;女生的侧影是从她左侧看过去的样子,叫“左视图”。
520 这个日子还在打比赛的你,也就抱着一棵二叉树左看看右看看了……
我们将二叉树的“侧影”定义为从一侧能看到的所有结点从上到下形成的序列。例如下图这棵二叉树,其右视图就是 { 1, 2, 3, 4, 5 },左视图就是 { 1, 6, 7, 8, 5 }。
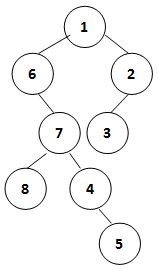
于是让我们首先通过一棵二叉树的中序遍历序列和后序遍历序列构建出一棵树,然后你要输出这棵树的左视图和右视图。
输入格式:
输入第一行给出一个正整数 N (≤20),为树中的结点个数。随后在两行中先后给出树的中序遍历和后序遍历序列。树中所有键值都不相同,其数值大小无关紧要,都不超过 int 的范围。
输出格式:
第一行输出右视图,第二行输出左视图,格式如样例所示。
输入样例:
8
6 8 7 4 5 1 3 2
8 5 4 7 6 3 2 1
输出样例:
R: 1 2 3 4 5
L: 1 6 7 8 5
#include <iostream>
#include <cstring>
using namespace std;
const int N=30;
int h[N],e[N],idx,ne[N];
int a[N],b[N];
int n,cnt,md;
void add(int a,int b)
{
e[++idx]=b;ne[idx]=h[a];h[a]=idx;
}
int build(int d,int l,int r)
{
int x=b[cnt--];
add(d,x);
md=max(md,d);
if(l==r) return a[l];
int pos=-1;
for(int i=l;i<=r;i++)
{
if(x==a[i]) {pos=i;break;}
}
if(pos+1<=r) build(d+1,pos+1,r);
if(pos-1>=l) build(d+1,l,pos-1);
return a[pos];
}
int main()
{
cin>>n; cnt=n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) cin>>b[i];
build(1,1,n);
cout << "R:";
for(int i=1;i<=md;i++)
{
int j=h[i];
while(ne[j]) j=ne[j];
cout<<" "<<e[j];
}
cout<<endl<<"L:";
for(int i=1;i<=md;i++)
cout<<" "<<e[h[i]];
}7-10 最短路计数
分数 10
全屏浏览
切换布局
作者 严华云
单位 湖州师范学院
给出一个 N 个顶点 M 条边的无向无权图,顶点编号为 1∼N。问从顶点 1 开始,到其他每个点的最短路有几条。
输入格式:
给出一个 N 个顶点 M 条边的无向无权图,顶点编号为 1∼N。问从顶点 1 开始,到其他每个点的最短路有几条。
输出格式:
输出 N 行,每行一个非负整数,第 i 行输出从顶点 1 到顶点 i 有多少条不同的最短路,由于答案有可能会很大,你只需要输出mod 100003后的结果即可。如果无法到达顶点 i 则输出 0。
输入样例:
5 7
1 2
1 3
2 4
3 4
2 3
4 5
4 5
输出样例:
1
1
1
2
4#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
typedef pair<int,int>pii;
const int N=100000+10,M=200000+10;
int h[N],e[M<<1],ne[M<<1],idx;
int dist[N];
int n,m;
bool st[N];
int res[N];
void add(int a,int b)
{
e[idx]=b;ne[idx]=h[a];h[a]=idx++;
}
void dijkstra()
{
priority_queue<pii,vector<pii>,greater<pii>>heap;
memset(dist,0x3f,sizeof(dist));
dist[1]=0;
res[1]=1;
heap.push({0,1});
while(!heap.empty())
{
auto t=heap.top();
int ver=t.second,d=t.first;
heap.pop();
if(!st[ver])
{
st[ver]=true;
for(int i=h[ver];i!=-1;i=ne[i])
{
int j=e[i];
if(dist[j]>=dist[ver]+1)
{
dist[j]=dist[ver]+ 1;
res[j]=(res[j]+res[ver])%100003;
// cout<<j<<" "<<res[j]<<endl;
heap.push({dist[j],j});
}
}
}
}
for(int i=1;i<=n;i++) cout<<res[i]<<endl;
}
int main()
{
cin>>n>>m;
memset(h,-1,sizeof(h));
while(m--)
{
int x,y;
cin>>x>>y;
add(x,y),add(y,x);
}
dijkstra();
}