二、二叉树Binary tree
文章目录
- 二、二叉树Binary tree
- 1.逻辑结构
- 1.1斜树
- 1.2满二叉树
- ❗1.3完全二叉树
- 1.4排序二叉树BST
- 1.5平衡二叉树AVL
- 1.6线索二叉树
- 2.性质
- 3.存储结构
- 3.1顺序存储
- 3.2链式存储
- 4.遍历
- 4.1前序遍历
- 4.1.1前序非递归方式
- 4.2中序遍历
- 4.2.1中序非递归方式
- 4.3后序遍历
- 4.3.1后序非递归方式
- 4.4递归求树的深度
- 4.5层序遍历
- 4.6由遍历序列构造二叉树
定义:
二叉树是一种特殊的树形结构,其特点是每个结点至多只有两棵子树(即二叉树中不存在度大于2的结点),并且二叉树的子树有左右之分,其次序不能任意颠倒。
与树相似,二叉树也以递归的形式定义。二叉树是n (n≥0) 个结点的有限集合:
- 或者为空二叉树,即n=0。
- 或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。
二叉树是有序树,若将其左、右子树颠倒,则成为另一棵不同的二叉树。即使树中结点只有一棵子树,也要区分它是左子树还是右子树。二叉树的5种基本形态如图所示。
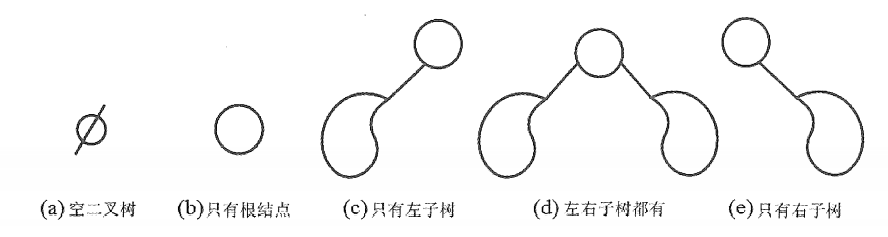
1.逻辑结构
1.1斜树
所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树。
1.2满二叉树
一棵高度为h,且含有 2 h − 1 2^h-1 2h−1个结点的二叉树。即树中的每层都含有最多的结点。
-
只有最后一层有叶子结点。
-
除叶子结点之外的每个结点度数均为 2,不存在度为 1 的结点。
-
可以对满二叉树按层序编号:约定编号从根结点(根结点编号为1)起,自上而下,自左向右。
这样,每个结点对应一个编号,对于编号为 i 的结点,若有双亲,则其双亲为 i 2 \cfrac i 2 2i,若有左孩子,则左孩子为 2i ;若有右孩子,则右孩子为 2i+1。

❗1.3完全二叉树
高度为h、有n个结点的二叉树,当且仅当其每个结点都与高度为h的满二叉树中编号为1~n的结点一一对应时,称为完全二叉树,如图所示。
如果像上图中红笔画的,因为缺失了一个结点而导致编号不吻合,那么就不是完全二叉树。
-
若 i ≤ n 2 i ≤ \cfrac n 2 i≤2n,则结点 i 为分支结点,否则为叶子结点。
-
叶子结点只可能在层次最大的两层(最下面两层)上出现。对于最大层次中的叶子结点,都依次排列在该层最左边的位置上。
-
最多有 1 个度为 1 的结点,只能有一个,且该结点只有左孩子而无右孩子。
度为 1 的结点个数 n 1 = { 1 , n 是偶数 0 , n 是奇数 度为1的结点个数n_1= \begin{cases} 1, &n是偶数\\[1ex] 0, &n是奇数\\ \end{cases} 度为1的结点个数n1={1,0,n是偶数n是奇数 -
按层序编号后,一旦出现某结点(编号为 i )为叶子结点或只有左孩子,则编号大于 i 的结点均为叶子结点。
-
若 n 为奇数,则每个分支结点都有左孩子和右孩子;
若 n 为偶数,则编号最大的分支结点(编号为 n 2 \cfrac n 2 2n)只有左孩子,没有右孩子,其余分支结点左、右孩子都有。即:
i 结点是 = { 分支结点 , i ≤ ⌊ n 2 ⌋ 叶子结点 , i > ⌊ n 2 ⌋ 度为 2 的结点个数 n 2 = { n 2 − 1 , n 是偶数 n 2 , n 是奇数 n 为偶数时候, n 1 存在。 叶子结点个数 n 0 = { n 2 , n 是偶数 n 2 + 1 , n 是奇数 i结点是= \begin{cases} 分支结点, & i≤ \lfloor \cfrac n 2\rfloor\\[1ex] 叶子结点, & i> \lfloor \cfrac n 2\rfloor\\ \end{cases} \\\\ 度为2的结点个数n_2= \begin{cases} \cfrac n 2 -1, &n是偶数\\[1ex] \cfrac n 2, &n是奇数\\ \end{cases} \\\\ n为偶数时候,n_1存在。 \\\\ 叶子结点个数n_0= \begin{cases} \cfrac n 2, &n是偶数\\[1ex] \cfrac n 2 +1, &n是奇数\\ \end{cases} i结点是=⎩ ⎨ ⎧分支结点,叶子结点,i≤⌊2n⌋i>⌊2n⌋度为2的结点个数n2=⎩ ⎨ ⎧2n−1,2n,n是偶数n是奇数n为偶数时候,n1存在。叶子结点个数n0=⎩ ⎨ ⎧2n,2n+1,n是偶数n是奇数
向下取整,表示奇数时和 奇数-1 的偶数时情况一样。可以看上图,n=12时,即使变为13,还是不能影响7变为分支节点。
-
同满二叉树按层序编号:约定编号从根结点(根结点编号为1)起,自上而下,自左向右。
这样,每个结点对应一个编号,对于编号为 i 的结点,若有双亲,则其双亲为 i 2 \cfrac i 2 2i,若有左孩子,则左孩子为 2i ;若有右孩子,则右孩子为 2i+1。
1.4排序二叉树BST
二叉排序树(Binary Sort Tree),又称二叉查找树(Binary Search Tree),二叉搜索树,排序二叉树。
它或者是一棵空二叉树,或者具有以下性质:
- 左子树上所有结点的关键字均小于根结点的关键字;
- 右子树上的所有结点的关键字均大于根结点的关键字;
- 左子树和右子树又各是一棵二叉排序树。

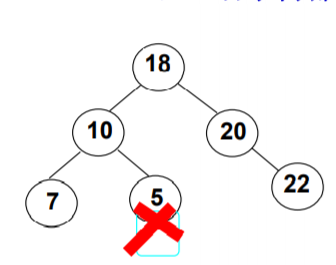
可以进行中序遍历,得到一个递增的序列。
适用于需要快速查找、插入和删除数据的场景。
插入和删除操作的时间复杂度为 O(log n),其中 n 是树中节点的个数。
查找操作的时间复杂度也为 O(log n) 在平均情况下,但在最坏情况下可能为 O(n)。
1.5平衡二叉树AVL
平衡二叉树(AVL树),它是 “平衡二叉搜索树” 的简称,它是一种二叉排序树。
它或者是一颗空树,或者是具有以下性质的二叉排序树:
- 它的左子树和左子树的高度之差(平衡因子)的绝对值不超过1;
- 且它的左子树和右子树又都是一颗平衡二叉树。
追求更好的平衡二叉树,可以得到更好的二叉排序树,提高排序和查询的效率,不至于让一边的树的深度太大。

1.6线索二叉树
每个节点除了左右子节点指针外,还包含两个线索指针:前驱指针和后继指针。可以通过线索指针进行前序、中序和后序遍历,而无需使用递归或栈等辅助工具。
左右子节点为空的指针指向相应的线索,而不是空指针。
适用于需要频繁进行遍历操作的场景,例如查找、排序等。
2.性质
-
任意一棵树,若结点数量为 n,则边的数量为 n−1。
-
非空二叉树上的叶子结点数 n 0 n_0 n0等于度为 2 的结点数加 1,即 n 0 = n 2 + 1 n_0=n_2+1 n0=n2+1。
我们设非空二叉树中度数为0,1,2的结点的个数分别为
n
0
,
n
1
,
n
2
n_0,n_1,n_2
n0,n1,n2,总结点数为n。
n
=
n
0
+
n
1
+
n
2
n
=
n
1
+
2
n
2
+
1
(
树的结点个数
=
所有结点的度数
+
1
)
↓
n
0
=
n
2
+
1
n=n_0+n_1+n_2\\ n=n_1+2n_2+1(树的结点个数=所有结点的度数+1)\\ ↓\\ n_0=n_2+1
n=n0+n1+n2n=n1+2n2+1(树的结点个数=所有结点的度数+1)↓n0=n2+1
-
二叉树中第 i 层上至多有 2 i − 1 2^{i-1} 2i−1 个结点(i≥1)。
m叉树中第 i 层上至多有 m i − 1 m^{i-1} mi−1 个结点(i≥1)。
-
高度为 h 的 二叉树 至多有 2 h − 1 2^h-1 2h−1 个结点(h≥1)(就是满二叉树)。
高度为 h 的 m叉树至多有 m h − 1 m − 1 \cfrac {m^h-1}{m-1} m−1mh−1个结点。
关于完全二叉树:
- n(n>0)个结点的完全二叉树层次(深度)为 ⌈ l o g 2 ( n + 1 ) ⌉ \lceil log_2(n+1) \rceil ⌈log2(n+1)⌉ 或 ⌊ l o g 2 n ⌋ + 1 \lfloor log_2n \rfloor +1 ⌊log2n⌋+1。
高为h的满二叉树共有
2
h
−
1
2^h-1
2h−1 个结点,就是完全二叉树能表示的最大。
高为h-1的满二叉树共有
2
h
−
1
−
1
2^{h-1}-1
2h−1−1 个结点,就是完全二叉树能表示的最小。

那么,结点个数应该在这两个范围之内:
2
h
−
1
−
1
<
n
≤
2
h
−
1
2
h
−
1
<
n
+
1
≤
2
h
h
−
1
<
l
o
g
2
n
+
1
≤
h
2^{h-1}-1 < n ≤ 2^h-1\\ 2^{h-1} < n+1 ≤ 2^h\\ h-1 < log_2{n+1} ≤ h
2h−1−1<n≤2h−12h−1<n+1≤2hh−1<log2n+1≤h
所以对中间的结果向上取整:
h
=
⌈
l
o
g
2
(
n
+
1
)
⌉
h=\left\lceil log_2(n+1) \right\rceil
h=⌈log2(n+1)⌉
【注意】在c语言中,默认是向下取整的,所以使用 ⌊ l o g 2 n ⌋ + 1 \lfloor log_2n \rfloor +1 ⌊log2n⌋+1会更方便。
对完全二叉树按从上到下、从左到右的顺序依次编号1,2…,n则有以下关系:
- i>1 时,结点 i 的双亲的编号为 i 2 \cfrac i 2 2i。i 为偶数时,它是双亲的左孩子;当 i 为奇数时,它是双亲的右孩子。
- 当 2i ≤ n 时(就是小于最大分支节点的结点: ⌊ n 2 ⌋ \lfloor \cfrac n 2\rfloor ⌊2n⌋),结点 i 的左孩子编号为 2i。否则无左孩子。
- 当 2i+1 ≤ n 时(就是小于最大分支节点的结点+1: ⌊ n 2 ⌋ + 1 \lfloor \cfrac n 2\rfloor+1 ⌊2n⌋+1),结点 i 的右孩子编号为 2i + 1 。否则无右孩子。
- 结点 i 所在层次(深度)为 l o g 2 i + 1 {log_2i}+ 1 log2i+1。
3.存储结构
- 顺序存储
- 链式存储
3.1顺序存储
二叉树的顺序存储是指用一组地址连续的存储单元依次自上而下、自左至右存储完全二叉树上的结点元素,即将完全二叉树上编号为 i 的结点元素存储在一维数组下标为 i-1 的分量中。
#define MaxSize 100
typedef char ElemType;
typedef struct
{
ElemType data[MaxSize]; // 存储树结点的数组
int BiTreeNum; // 二叉树的结点个数
}SqBiTree;
关于完全二叉树结点 i 总结:

- 左孩子:2i。
- 右孩子:2i+1。
- 双亲: ⌊ i 2 ⌋ \lfloor \cfrac i 2\rfloor ⌊2i⌋(因为右孩子是奇书,除以2有余数,余数取整的时候删去)。
- 结点所在层次: ⌈ l o g 2 ( n + 1 ) ⌉ \lceil log_2(n+1) \rceil ⌈log2(n+1)⌉ 或 ⌊ l o g 2 n ⌋ + 1 \lfloor log_2n \rfloor +1 ⌊log2n⌋+1。
判断:
- i是否有左孩子:2i ≤ n?
- i是否有右孩子:2i+1 ≤ n?
- i是否是叶子结点:i > ⌊ i 2 ⌋ \lfloor \cfrac i 2\rfloor ⌊2i⌋?
【注意】如果不是完全二叉树,是不同二叉树,则不行。

但是可以把原完全二叉树不存在的结点看作null,使得他们的编号对应起来。

这时候判断结点有无,只能使用isEmpty来判断。
缺点:存储空间浪费。
所以依据二叉树的性质,完全二叉树和满二叉树采用顺序存储比较合适,树中结点的序号可以唯一地反映结点之间的逻辑关系,这样既能最大可能地节省存储空间,又能利用数组元素的下标值确定结点在二叉树中的位置,以及结点之间的关系。
但对于一般的二叉树,为了让数组下标能反映二叉树中结点之间的逻辑关系,只能添加一些并不存在的空结点,让其每个结点与完全二叉树上的结点相对照,再存储到一维数组的相应分量中。
最坏情况下,高度h且只有h个结点的单支树(所有结点只有右孩子),也至少需要2h-1个存储单元
所以这种顺序存储结构只适合完全二叉树,这样空间才不浪费。
3.2链式存储
既然顺序存储适用性不强,我们就要考虑链式存储结构。
二叉树每个结点最多有两个孩子,所以为它设计一个数据域和两个指针域是比较自然的想法,我们称这样的链表叫做二叉链表。
| lchild | data | rchild |
|---|
//二叉树的结点(二叉链表)
typedef struct BiTNode{
ElemType data; //数据域
struct BiTNode *lchild,*rchild; //左、右孩子指针
}BiTNode,*BiTree;
容易验证,在含有 n 个结点的二叉链表中,含有 n+1 个空域。

这里的 n+1个空指针域,其实可以利用起来,在后面用于构造线索二叉树。
struct ElemType{
int value;
};
//二叉树的结点(二叉链表)
typedef struct BiTNode{
ElemType data;
struct BiTNode *lchild, *rchild;
}BiTNode,*BiTree;
//定义一棵空树
BiTree root = NULL;
//插入根节点root
root = (BiTree)malloc(sizeof(BiTNode));
root->data = {1};
root->lchild = NULL;
root->rchild = NULL;
//插入新结点
BiTNode *p = (BiTNode*)malloc(sizeof(BiTNode));
p->data = {2};
p->lchild = NULL;
p->rchild = NULL;
root->lchild = p;//作为根节点的左孩子
前序遍历递归法建立二叉树算法
// 前序遍历递归法建立二叉树算法
BiTree CreatBiTree(){
BiTree T;
ElemType data;
fflush(stdin);
scanf("%c",&data);
if(data == '#')
T = NULL;
else{
T = (BiTree)malloc(sizeof(BiNode));
T->data = data;
printf("%c的左子树:",data);
T->lchild = CreatBiTree();
printf("%c的右子树:",data);
T->rchild = CreatBiTree();
}
return T;
}
二叉链表这样找孩子结点很简单,但是找父节点很麻烦。所以再添加父结点指针*parent构成三叉链表。
//二叉树的结点(三叉链表)
typedef struct BiTNode{
ElemType data; //数据域
struct BiTNode *lchild,*rchild; //左、右孩子指针
struct BiTNode *parent; //父结点指针
}BiTNode,*BiTree;
4.遍历
先/中/后序遍历:根据二叉树的递归特性进行的遍历。一般来说分为如下三种:

以二叉链表为例:
4.1前序遍历
前序遍历,先序遍历(Pre-Order Traversal,根 - 左 - 右,N-L-R):指先访问根,然后访问子树的遍历方式
//先序遍历
void Pre0rder(BiTree T){
if(T!=NULL){
visit(T)//访问根结点,比如打印
PreOrder(T->lchild);//递归遍历左子树
Pre0rder(T->rchild);//递归遍历右子树
}
}
4.1.1前序非递归方式
(先序遍历和中序遍历的基本思想是类似的,只需把访问结点操作放在入栈操作的前面。)
void PreOrder2(BiTree T){
InitStack(S); //初始化栈S
BiTNode* p = T; //p是遍历指针
while(p || !IsEmpty(S)){ //栈不空或p不空时循环
if(p){
visit(p); //访问出栈结点
Push(S, p); //当前节点入栈
p = p->lchild; //左孩子不空,一直向左走
}else{
Pop(S, p); //栈顶元素出栈
p = p->rchild; //向右子树走,p赋值为当前结点的右孩子
}
}
}
4.2中序遍历
中序遍历(In-Order Traversal, 左 - 根 - 右,LNR):指先访问左(右)子树,然后访问根,最后访问右(左)子树的遍历方式。
中序遍历一般是用二叉树实现:
//中序遍历
void In0rder(BiTree T){
if(T!=NULL){
InOrder(T->lchild);//递归遍历左子树
visit(T)//访问根结点,比如打印
In0rder(T->rchild);//递归遍历右子树
}
}
4.2.1中序非递归方式
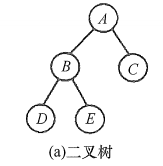
借助栈,我们来分析中序遍历的访问过程:
- 沿着根的左孩子,依次入栈,直到左孩子为空,说明已找到可以输出的结点,此时栈内元素依次为ABD。
- 栈顶元素出栈并访问:
- 若其右孩子为空,继续执行步骤2;
- 若其右孩子不空,将右子树转执行步骤1。
栈顶D出栈并访问,它是中序序列的第一个结点。D右孩子为空,栈顶B出栈并访问。B右孩子不空,将其右孩子E入栈,E左孩子为空,栈顶E出栈并访问。E右孩子为空,栈顶A出栈并访问。A右孩子不空,将其右孩子C入栈,C左孩子为空,栈顶C出栈并访问。由此得到中序序列DBEAC。
根据分析可以写出中序遍历的非递归算法如下:
void InOrder2(BiTree T){
InitStack(S); //初始化栈S
BiTNode* p = T; //p是遍历指针
while(p || !IsEmpty(S)){ //栈不空或p不空时循环
if(p){
Push(S, p); //当前节点入栈
p = p->lchild; //左孩子不空,一直向左走
}else{
Pop(S, p); //栈顶元素出栈
visit(p); //访问出栈结点
p = p->rchild; //向右子树走,p赋值为当前结点的右孩子
}
}
}
4.3后序遍历
后序遍历(Post-Order Traversal, 左 - 右 - 根,LRN):指先访问子树,然后访问根的遍历方式
//后序遍历
void Post0rder(BiTree T){
if(T!=NULL){
PostOrder(T->lchild);//递归遍历左子树
Post0rder(T->rchild);//递归遍历右子树
visit(T)//访问根结点,比如打印
}
}
三种遍历算法中,递归遍历左、右子树的顺序都是固定的,只是访问根结点的顺序不同。不管采用哪种遍历算法,每个结点都访问一次且仅访问一次,故时间复杂度都是O(n)。
在递归遍历中,递归工作栈的栈深恰好为树的深度,所以在最坏情况下,二叉树是有n个结点且深度为n的单支树,遍历算法的空间复杂度为O(n)。
4.3.1后序非递归方式
后序遍历的非递归实现是三种遍历方法中最难的。因为在后序遍历中,要保证左孩了和右孩子都已被访问并且左孩子在右孩子前访问才能访问根结点,这就为流程的控制带来了难题。
算法思想:后序非递归遍历二叉树是先访问左子树,再访问右子树,最后访问根结点。
- 沿着根的左孩子,依次入栈,直到左孩子为空。此时栈内元素依次为ABD。
- 读栈顶元素:
- 若其右孩子不空且未被访问过,将右子树转执行①;
- 否则,栈顶元素出栈并访问。
栈顶D的右孩子为空,出栈并访问,它是后序序列的第一个结点;栈顶B的右孩子不空且未被访问过,E入栈,栈顶E的左右孩子均为空,出栈并访问;栈顶B的右孩子不空但已被访问,B出栈并访问;栈项A的右孩子不空且未被访问过,C入栈,栈项C的左右孩子均为空,出栈并访问;栈顶A的右孩子不空但已被访问,A出栈并访问。由此得到后序序列DEBCA。
在上述思想的第②步中,必须分清返回时是从左子树返回的还是从右子树返回的,因此设定一个辅助指针r,指向最近访问过的结点。也可在结点中增加一个标志域,记录是否已被访问。
后序遍历的非递归算法如下:
void PostOrder2(BiTree T){
InitStack(S);
BiTNode* p = T, r = NULL;
while(p || !IsEmpty(S)){
if(p){ //走到最左边
push(S, p);
p = p->lchild;
}else{ //向右
GetTop(S, p); //读栈顶元素(非出栈)
//若右子树存在,且未被访问过
if(p->rchild && p->rchild != r){
p = p->rchild; //转向右
push(S, p); //压入栈
p = p->lchild; //再走到最左
}else{ //否则,弹出结点并访问
pop(S, p); //将结点弹出
visit(p->data); //访问该结点
r = p; //记录最近访问过的结点
p = NULL;
}
}
}
}
4.4递归求树的深度
可以先测出左右子树的深度,然后+1,就是加上根节点,那么就是此树的高度,通过递归的方法,依次求出子树高度,然后得到最高的。
int treeDepth(BiTree T){
if (T ==NULL) {
return 0;
}else {
int l=treeDepth(T->lchild);
int r=treeDepth(T->rchild);
//树的深度=Max(左子树深度,右子树深度)+1
return l>r ? l+1 : r+1;
}
}
4.5层序遍历
层次遍历,即按照箭头所指方向,按照1,2,3,4的层次顺序,一层一层地对二叉树进行遍历。

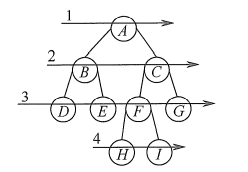
算法思想:
-
初始化一个辅助队列;
-
根结点入队;
-
若队列非空,则队头结点出队,访问该结点。并将其左、右孩子插入队尾(先左再右,如果有的话);
即:每出队一个结点,就把它的孩子放入结点。
-
重复③直至队列为空;
这里使用链队列。
//按层遍历递归二叉树算法
// 每出队一个结点,就把它的孩子放入结点。
void Layer_order(BiTree T)
{
LinkQueue Q; //定义辅助队列
InitQueue(&Q); //初始化辅助队列
// 注意判断是不是NULL
if(T != NULL){
EnQueue(&Q, T); //将根节点入队
}
while(!QueueEmpty(Q)){ //队列不空则循环
BiNode* temp = DeQueue(&Q);
printf("%3c", visit(temp)); //访问出队结点
//两种判断是否为空结点
if(temp->lchild != NULL){
EnQueue(&Q, temp->lchild); //左子树不空,则左子树根节点入队
}
if(temp->rchild){
EnQueue(&Q, temp->rchild); //右子树不空,则右子树根节点入队
}
}
}
4.6由遍历序列构造二叉树
若只给出一棵二叉树的前/中/后/层序遍历序列中的一种,不能唯一确定一棵二叉树。
一个中序遍历,因为不同根节点,可以有不同的二叉树实现。

所以使用前、后遍历确定根节点,使用中序遍历划分左右子树,来确定唯一的二叉树。
由二叉树的先序序列和中序序列可以唯一地确定一棵二叉树。
(先序+中序)
在先序遍历序列中,第一个结点一定是二叉树的根结点;而在中序遍历中,根结点必然将中序序列分割成两个子序列,前一个子序列是根结点的左子树的中序序列,后一个子序列是根结点的右子树的中序序列。根据这两个子序列,在先序序列中找到对应的左子序列和右子序列。
在先序序列中,左子序列的第一个结点是左子树的根结点,右子序列的第一个结点是右子树的根结点。如此递归地进行下去,便能唯一地确定这棵二叉树
同理,由二叉树的后序序列和中序序列也可以唯一地确定一棵二叉树。
(后序+中序)
因为后序序列的最后一个结点就如同先序序列的第一个结点,可以将中序序列分割成两个子序列,然后采用类似的方法递归地进行划分,进而得到一棵二叉树。
由二叉树的层序序列和中序序列也可以唯一地确定一棵二叉树。
(层序+中序)
【注意】前序、后序、层序序列两两组合,都不能确定唯一的二叉树。只有中序存在才可以。
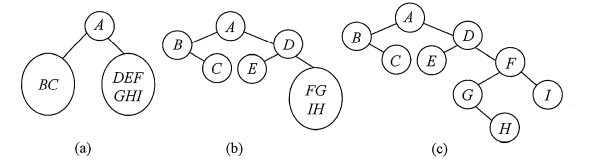
例如,求先序序列(ABCDEFGH)和中序序列(BCAEDGHFI)所确定的二叉树。
首先,由先序序列可知A为二叉树的根结点。中序序列中A之前的BC为左子树的中序序列,EDGHFI为右子树的中序序列。然后由先序序列可知B是左子树的根结点,D是右子树的根结点。以此类推,就能将剩下的结点继续分解下去,最后得到的二叉树如图c所示。
















![[ACM MM 2024] AesExpert 面向图像审美知觉的多模态基础模型](https://i-blog.csdnimg.cn/direct/d4bc7caa707642a384456697e0e75de7.png)