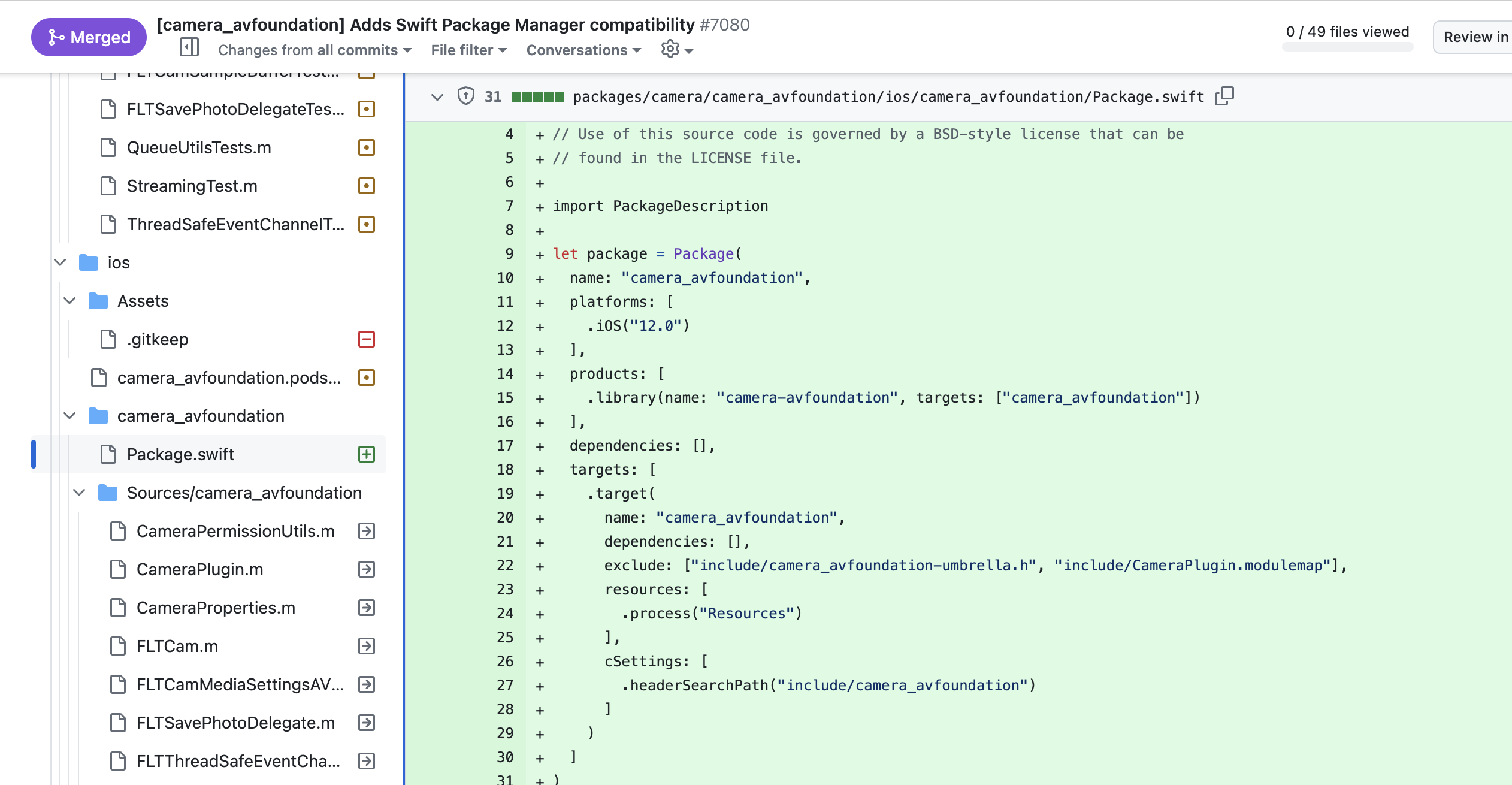
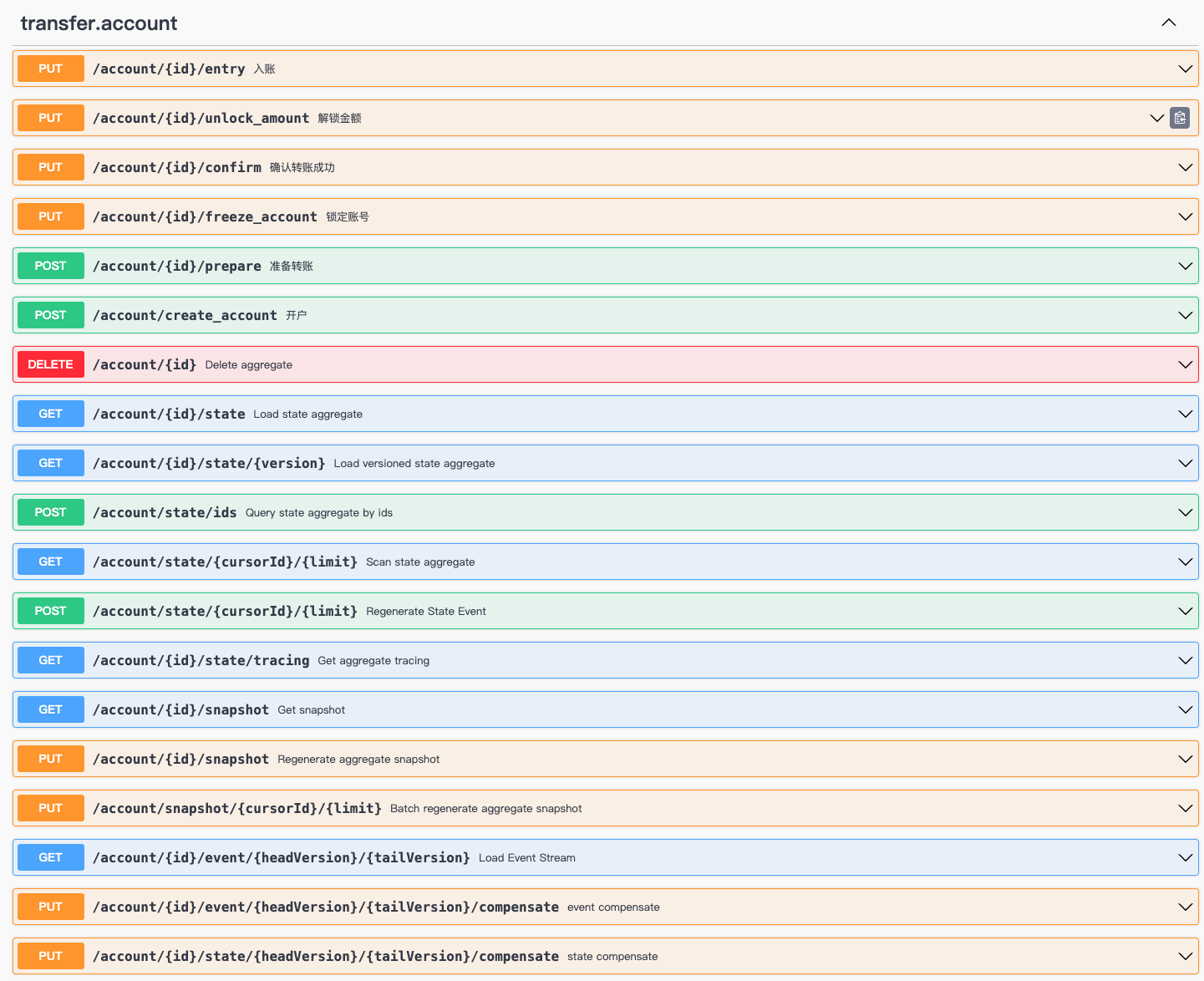
题目：

题解：

#define FATHER_NODE(i)      (0 == (i) ? -1 : ((i) - 1 >> 1))
#define LEFT_NODE(i)        (((i) << 1) + 1)
#define RIGHT_NODE(i)       (((i) << 1) + 2)

/* 优先队列（小根堆）。 */
typedef struct
{
    int *arr;
    int arrSize;
}
PriorityQueue;

/* 二进制树（01字典树）。 */
typedef struct
{
    int *arr;
    int highestBit;
}
BinaryTree;

/* 几个自定义函数的声明，具体实现见下。 */
static void queuePush(PriorityQueue *queue, long long *prefix, int x);
static void queuePop(PriorityQueue *queue, long long *prefix);
static int treeHighestBit(int mostVal);
static void treePush(BinaryTree *tree, int x);
static void treePop(BinaryTree *tree, int x);
static int treeSmaller(BinaryTree *tree, int x);

/* 主函数：
  treeSize:         二进制树的数组空间大小，等于里面最大值的3倍，具体证明略，大致就是等比数列求和的结果。
  prefix[]:         其中prefix[x]表示[0, x]范围内子数组的前缀和。这里必须以long long类型存储。
  window[]:         里面存储prefix[]数组的下标，即prefix[window[x]]才真正表示一个前缀和。
  buff1[],buff2[]:  优先队列与二进制树各自使用的数组空间。其中buff2[]必须初始化为全0。
  queue:            优先队列（小根堆），为了不打乱prefix[]数组中的数值顺序，而且window[]数组中实际存放的是下标，所以借用堆排序。
  tree:             二进制树（01字典树）。 */
int countRangeSum(int *nums, int numsSize, int lower, int upper)
{
    const int treeSize = numsSize * 3;
    int x = 0, y = 0, z = 0, t = 0, result = 0;
    long long sum = 0;
    long long prefix[numsSize];
    int window[numsSize], buff1[numsSize], buff2[treeSize];
    PriorityQueue queue;
    BinaryTree tree;
    /* 初始化。 */
    queue.arr = buff1;
    queue.arrSize = 0;
    memset(buff2, 0, sizeof(buff2));
    tree.arr = buff2;
    tree.highestBit = treeHighestBit(numsSize - 1);
    /* 计算前缀和，并将前缀和的下标放到一个小根堆里面，小根堆里面以对应的前缀和为优先级。 */
    for(x = 0; numsSize > x; x++)
    {
        sum += nums[x];
        prefix[x] = sum;
        queuePush(&queue, prefix, x);
        /* 如果[0, x]的子数组和本来就在[lower, upper]之间，计数累计。 */
        if((long long)lower <= sum && (long long)upper >= sum)
        {
            result++;
        }
    }
    /* 将前缀和数组的下标，以对应的prefix值从小到大的顺序，放到window数组中。 */
    while(0 < queue.arrSize)
    {
        window[t] = queue.arr[0];
        t++;
        queuePop(&queue, prefix);
    }
    /* 开始以滑动窗口的形式移动窗口的左右指针。 */
    for(x = 0; numsSize > x; x++)
    {
        /* 将所有prefix[window[x]] - prefix[window[y]] >= lower的下标y都加入。 */
        while(numsSize > y && prefix[window[x]] - lower >= prefix[window[y]])
        {
            treePush(&tree, window[y]);
            y++;
        }
        /* 将所有prefix[window[x]] - prefix[window[z]] > upper的下标z都移除。 */
        while(numsSize > z && prefix[window[x]] - upper > prefix[window[z]])
        {
            treePop(&tree, window[z]);
            z++;
        }
        /* 将窗口内（树内）剩余的下标值中，小于window[x]的数量加到结果中。 */
        t = treeSmaller(&tree, window[x]);
        result += t;
    }
    return result;
}

/* 小根堆的push操作。由于堆中存储的是prefix[]数组的下标，所以入参需带上prefix。 */
static void queuePush(PriorityQueue *queue, long long *prefix, int x)
{
    int son = queue->arrSize, father = FATHER_NODE(son);
    /* 新加入数值之后，数量加一。 */
    queue->arrSize++;
    /* 根据对应prefix[]值的大小关系，调整父子节点的位置。 */
    while(-1 != father && prefix[x] < prefix[queue->arr[father]])
    {
        queue->arr[son] = queue->arr[father];
        son = father;
        father = FATHER_NODE(son);
    }
    /* 放到实际满足父子节点大小关系的位置。 */
    queue->arr[son] = x;
    return;
}

/* 小根堆的pop操作。由于堆中存储的是prefix[]数组的下标，所以入参需带上prefix。 */
static void queuePop(PriorityQueue *queue, long long *prefix)
{
    int father = 0, left = LEFT_NODE(father), right = RIGHT_NODE(father), son = 0;
    /* 堆顶pop之后，数量减一。默认将堆尾的数值补充上来填补空位。 */
    queue->arrSize--;
    /* 根据对应prefix[]值的大小关系，调整父子节点的位置。 */
    while((queue->arrSize > left && prefix[queue->arr[queue->arrSize]] > prefix[queue->arr[left]])
        || (queue->arrSize > right && prefix[queue->arr[queue->arrSize]] > prefix[queue->arr[right]]))
    {
        son = (queue->arrSize > right && prefix[queue->arr[left]] > prefix[queue->arr[right]]) ? right : left;
        queue->arr[father] = queue->arr[son];
        father = son;
        left = LEFT_NODE(father);
        right = RIGHT_NODE(father);
    }
    /* 放到实际满足父子节点大小关系的位置。 */
    queue->arr[father] = queue->arr[queue->arrSize];
    return;
}

/* 计算二进制树中，可能出现的最大的数值，所占据的最高二进制比特。
  比如，最大值的二进制是101100(b)，那么返回的最高比特是100000(b)。特殊的，最大是0的时候返回1(b)。 */
static int treeHighestBit(int mostVal)
{
    int x = 1;
    if(0 < mostVal)
    {
        while(0 < mostVal)
        {
            x++;
            mostVal = mostVal >> 1;
        }
        x = 1 << x - 2;
    }
    return x;
}

/* 往二进制树中push一个数值。 */
static void treePush(BinaryTree *tree, int x)
{
    int i = 0, bit = tree->highestBit;
    /* 从最高位到最低位的顺序，该位为1就给右分支加1，为0就给左分支加1。 */
    while(0 < bit)
    {
        i = (bit & x) ? RIGHT_NODE(i) : LEFT_NODE(i);
        tree->arr[i]++;
        bit = bit >> 1;
    }
    return;
}

/* 从二进制树中pop一个数值。 */
static void treePop(BinaryTree *tree, int x)
{
    int i = 0, bit = tree->highestBit;
    /* 从最高位到最低位的顺序，该位为1就给右分支减1，为0就给左分支减1。 */
    while(0 < bit)
    {
        i = (bit & x) ? RIGHT_NODE(i) : LEFT_NODE(i);
        tree->arr[i]--;
        bit = bit >> 1;
    }
    return;
}

/* 在二进制树中查找比输入数值小的数值数量。 */
static int treeSmaller(BinaryTree *tree, int x)
{
    int i = 0, bit = tree->highestBit, result = 0;
    /* 从高位到低位的顺序查看。 */
    while(0 < bit)
    {
        /* 该位为1，则肯定比高位相同，该位为0的数值更大，即把左分支的数量加到结果中。 */
        if(bit & x)
        {
            result += tree->arr[LEFT_NODE(i)];
            i = RIGHT_NODE(i);
        }
        /* 该位为0，就往左分支走，不做任何其它处理。 */
        else
        {
            i = LEFT_NODE(i);
        }
        bit = bit >> 1;
    }
    return result;
}