第九章 动态规划part01
今天正式开始动态规划!
理论基础
无论大家之前对动态规划学到什么程度,一定要先看 我讲的 动态规划理论基础。
如果没做过动态规划的题目,看我讲的理论基础,会有感觉 是不是简单题想复杂了?
其实并没有,我讲的理论基础内容,在动规章节所有题目都有运用,所以很重要!
如果做过动态规划题目的录友,看我的理论基础 就会感同身受了。
https://programmercarl.com/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html
视频:https://www.bilibili.com/video/BV13Q4y197Wg
509. 斐波那契数
很简单的动规入门题,但简单题使用来掌握方法论的,还是要有动规五部曲来分析。
https://programmercarl.com/0509.%E6%96%90%E6%B3%A2%E9%82%A3%E5%A5%91%E6%95%B0.html
视频:https://www.bilibili.com/video/BV1f5411K7mo
70. 爬楼梯
本题大家先自己想一想, 之后会发现,和 斐波那契数 有点关系。
https://programmercarl.com/0070.%E7%88%AC%E6%A5%BC%E6%A2%AF.html
视频:https://www.bilibili.com/video/BV17h411h7UH
746. 使用最小花费爬楼梯
这道题目力扣改了题目描述了,现在的题目描述清晰很多,相当于明确说 第一步是不用花费的。
更改题目描述之后,相当于是 文章中 「拓展」的解法
https://programmercarl.com/0746.%E4%BD%BF%E7%94%A8%E6%9C%80%E5%B0%8F%E8%8A%B1%E8%B4%B9%E7%88%AC%E6%A5%BC%E6%A2%AF.html
视频讲解:https://www.bilibili.com/video/BV16G411c7yZ
动规五步曲 你给我记住了,用几道简单题目来掌握方法论
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
比较考究,01 先遍历背包,后遍历物品。
4.1排列和组合的遍历顺序是不相同的。
4.1.1 排列:背包在外 物品在内。(322)
4.1.2 组合:物品在外,背包在内。(518)- 举例推导dp数组
(出现问题,打印dp数组,检查是否有问题,检验1 2 3 4 步骤)
509. 斐波那契数
题目链接
https://leetcode.cn/problems/fibonacci-number/description/
解题思路
用一道简单题目来掌握方法论,动规五步曲
1.确定dp数组和下标的含义
dp[i] 解读
下标i表示第i个斐波那契数,dp[i] 表示第i个斐波那契数的值
2.确定递推公式
这题简单,题目已经告诉了我们递推公式是什么
dp[i]=dp[i-1] + dp[i-2]
3.dp数组如何初始化
这题简单,题目已经告诉我们了
dp[0]=0 ,dp[1]=1
4.确定遍历顺序
我们发现d[i]是从dp[i-1]和dp[i-2]得到的,那么我们就要从前向后遍历才能得到dp[i]的结果
5.打印dp数组
主要用来debug的,如何验证我们写的代码没有问题呢,就是要把dp数组打印出来验证和我们想象的数组是否一样
code
class Solution {
//时间复杂度O(n) 空间复杂度O(n)
public int fib1(int n) {
if(n<=1){
return n;
}
//1.确定dp数组以及下标的含义
//dp[i]的定义为:第i个数的斐波那契数值是dp[i]
//2.确定递推公式
//状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];
//3.dp数组初始化
int[] dp=new int[n+1];
dp[0]=0;
dp[1]=1;
//4.确定遍历顺序
for(int i=2;i<=n;i++){
dp[i]=dp[i-1]+dp[i-2];
}
//按照这个递推公式dp[i] = dp[i - 1] + dp[i - 2],我们来推导一下,当n为10的时候,dp数组应该是如下的数列:
//0 1 1 2 3 5 8 13 21 34 55
//如果代码写出来,发现结果不对,就把dp数组打印出来看看和我们推导的数列是不是一致的。
//5.打印dp数组
//System.out.println(Arrays.toString(dp));
return dp[n];
}
}
优化空间复杂度,只用长度为2的dp数组
//时间O(n) 优化为空间(O)1
public int fib(int n) {
if(n<=1){
return n;
}
int[] dp=new int[2];
dp[0]=0;
dp[1]=1;
for(int i=2;i<=n;i++){
int sum=dp[0]+dp[1];
dp[0]=dp[1];
dp[1]=sum;
}
return dp[1];
}
递归写法 非常耗时
- 时间复杂度:O(2^n) 空间复杂度:O(n),算上了编程语言中实现递归的系统栈所占空间
- 递归写法时间复杂度非常高 画出来是一个树,一棵深度(按根节点深度为1)为k的二叉树最多可以有 2^k - 1 个节点 O(2^n)
好好看看这几篇文章分析递归的时间复杂度
https://programmercarl.com/%E5%89%8D%E5%BA%8F/%E9%80%92%E5%BD%92%E7%AE%97%E6%B3%95%E7%9A%84%E6%97%B6%E9%97%B4%E4%B8%8E%E7%A9%BA%E9%97%B4%E5%A4%8D%E6%9D%82%E5%BA%A6%E5%88%86%E6%9E%90.html
x的n次方
https://programmercarl.com/%E5%89%8D%E5%BA%8F/%E9%80%9A%E8%BF%87%E4%B8%80%E9%81%93%E9%9D%A2%E8%AF%95%E9%A2%98%E7%9B%AE%EF%BC%8C%E8%AE%B2%E4%B8%80%E8%AE%B2%E9%80%92%E5%BD%92%E7%AE%97%E6%B3%95%E7%9A%84%E6%97%B6%E9%97%B4%E5%A4%8D%E6%9D%82%E5%BA%A6%EF%BC%81.html
public int fib2(int n){
if(n<=1){
return n;
}
return fib2(n-1)+fib2(n-2);
}
70. 爬楼梯
题目链接
https://leetcode.cn/problems/climbing-stairs/description/
解题思路
多举几个例子,就可以发现其规律。
爬到第一层楼梯有一种方法,爬到二层楼梯有两种方法。
那么第一层楼梯再跨两步就到第三层 ,第二层楼梯再跨一步就到第三层。
所以到第三层楼梯的状态可以由第二层楼梯 和 到第一层楼梯状态推导出来,那么就可以想到动态规划了。我们来分析一下,动规五部曲:
定义一个一维数组来记录不同楼层的状态
1.确定dp数组以及下标的含义
dp[i]: 爬到第i层楼梯,有dp[i]种方法2.确定递推公式
如何可以推出dp[i]呢?
从dp[i]的定义可以看出,dp[i] 可以有两个方向推出来。
首先是dp[i - 1],上i-1层楼梯,有dp[i - 1]种方法,那么再一步跳一个台阶不就是dp[i]了么。
还有就是dp[i - 2],上i-2层楼梯,有dp[i - 2]种方法,那么再一步跳两个台阶不就是dp[i]了么。
那么dp[i]就是 dp[i - 1]与dp[i - 2]之和!
所以dp[i] = dp[i - 1] + dp[i - 2] 。
在推导dp[i]的时候,一定要时刻想着dp[i]的定义,否则容易跑偏。
这体现出确定dp数组以及下标的含义的重要性!3.dp数组如何初始化
dp[1]=1 dp[2]=2,然后从i = 3开始递推,这样才符合dp[i]的定义。
4.确定遍历顺序
从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,遍历顺序一定是从前向后遍历的
5.举例推导dp数组
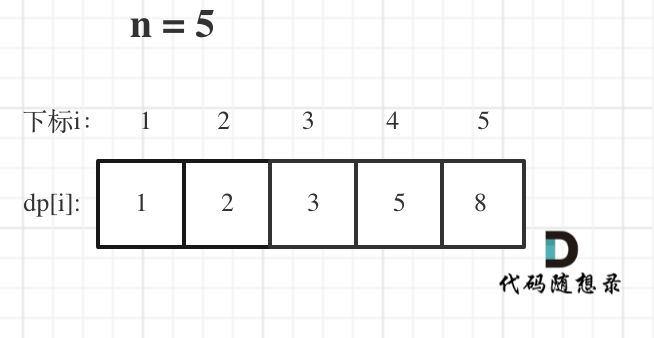
举例当n为5的时候,dp table(dp数组)应该是这样的
如果代码出问题了,就把dp table 打印出来,看看究竟是不是和自己推导的一样。
code
class Solution {
public int climbStairs(int n) {
if(n<=1){
return n;
}
//1.确定dp数组以及下标的含义
//dp[i]: 爬到第i层楼梯,有dp[i]种方法
//2.确定递推公式
//dp[i]=dp[i-1]+dp[i-2] dp[i-1]爬一个台阶到dp[i] dp[i-2]爬俩个台阶到dp[i] dp[3]=dp[2]+dp[1] 慢慢往上计算递推
//3.dp数组如何初始化
int[] dp=new int[n+1];
dp[1]=1;
dp[2]=2;
//4.确定遍历顺序 后边有前边递推出结果,从前向后遍历
for(int i=3;i<=n;i++){
dp[i]=dp[i-1]+dp[i-2];
}
//5.举例推导dp数组
//System.out.println(Arrays.toString(dp));
return dp[n];
}
}
优化空间(O)1
后面将讲解的很多动规的题目其实都是当前状态依赖前两个,或者前三个状态,都可以做空间上的优化,但我个人认为面试中能写出版本一就够了哈,清晰明了,如果面试官要求进一步优化空间的话,我们再去优化。
因为版本一才能体现出动规的思想精髓,递推的状态变化。
int climbStairs(int n) {
if (n <= 1) return n;
int[] dp=new int[3];
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) {
int sum = dp[1] + dp[2];
dp[1] = dp[2];
dp[2] = sum;
}
return dp[2];
}
746. 使用最小花费爬楼梯
题目链接
https://leetcode.cn/problems/min-cost-climbing-stairs/description/
解题思路
1.确定dp数组以及下标的含义
** dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]。**
** 2.确定递推公式**
** 可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]。**
** dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。**
** dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。**
** 那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢?**
** 一定是选最小的,所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);**
3.如何初始化数组
只初始化dp[0]和dp[1] 其他均递推出来
新题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。”也就是说 到达 第 0 个台阶是不花费的,但从 第 0 个台阶 往上跳的话,需要花费 cost[0]。
所以初始化 dp[0] = 0,dp[1] = 0;
4.确定遍历顺序
** dp[i]由dp[i-1]dp[i-2]推出,所以是从前到后遍历cost数组就可以了**
** 5.举例推导dp数组 **
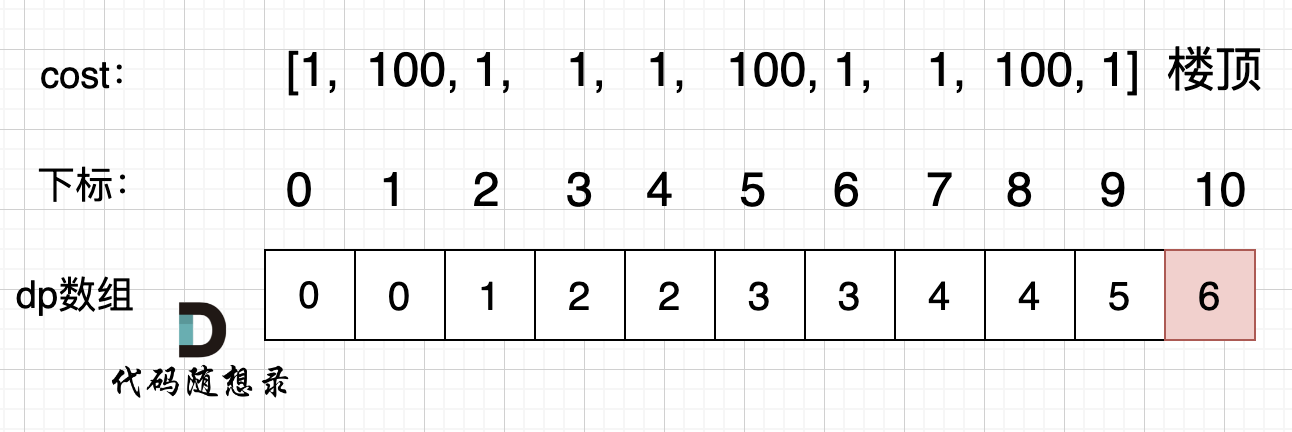
拿示例2:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ,来模拟一下dp数组的状态变化,如下
code
class Solution {
public int minCostClimbingStairs(int[] cost) {
//1.确定dp数组以及下标的含义
//dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]。
//2.确定递推公式
//可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]。
// dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。
// dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
// 那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢?
// 一定是选最小的,所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
//3.如何初始化数组
//只初始化dp[0]和dp[1] 其他均递推出来
//新题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。”
// 也就是说 到达 第 0 个台阶是不花费的,但从 第 0 个台阶 往上跳的话,需要花费 cost[0]。
//所以初始化 dp[0] = 0,dp[1] = 0;
int n=cost.length;
int[] dp=new int[n+1];
dp[0]=0;
dp[1]=0;
//4.确定遍历顺序
//dp[i]由dp[i-1]dp[i-2]推出,所以是从前到后遍历cost数组就可以了
for(int i=2;i<=n;i++){
dp[i]=Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
}
//5.举例推导dp数组 ,拿示例2:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ,来模拟一下dp数组的状态变化,如下
//System.out.println(Arrays.toString(dp));
return dp[n];
}
}