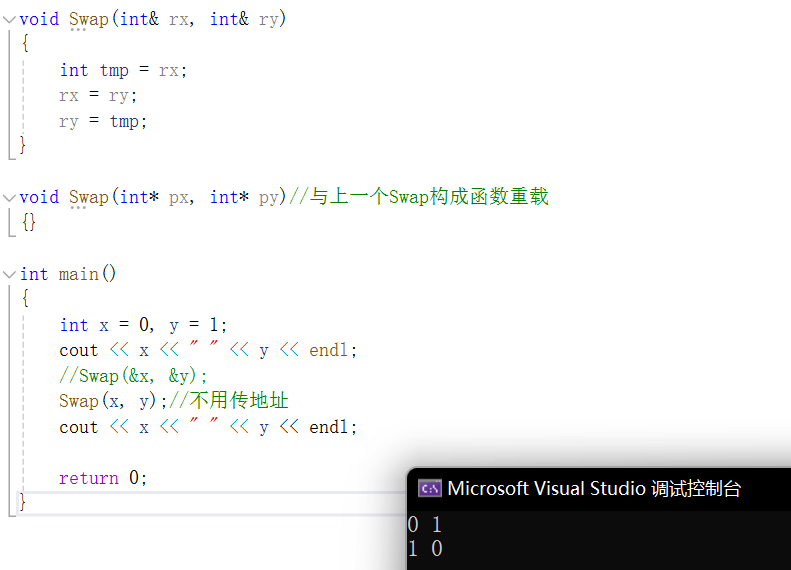
自定义线性滤波
- 原理
- 相关
- 卷积核
- 线性滤波操作
- API
- 实例
原理
相关
线性滤波的是指就是相关,即计算图像中的每个部分和卷积核(kernel)的相关结果。
卷积核
卷积核本质上是一个固定大小的系数数组,数组中的某个元素被作为锚点(一般是数组的中心),如下图:

线性滤波操作
上面讲了线性滤波的实质就是计算相关,相关计算的具体步骤如下:
- 将卷积核的锚点放在某个目标像素上,卷积核的其他部分就会覆盖目标像素的邻近像素;
- 将卷积核上的系数与被覆盖的像素的值相乘,然后将积加总;
- 将加总的和赋予目标像素
- 对图像上的所有像素都应用以上步骤,直到每个像素都被当作目标像素进行了计算。
用数学公式来表示以上步骤:
H
(
x
,
y
)
=
∑
i
=
0
M
i
−
1
∑
j
=
0
M
j
−
1
I
(
x
+
i
−
a
i
,
y
+
j
−
a
j
)
K
(
i
,
j
)
H(x,y)=\displaystyle \sum_{i=0}^{M_i-1} \displaystyle \sum_{j=0}^{M_j-1} I(x+i-a_i, y+j-a_j)K(i, j)
H(x,y)=i=0∑Mi−1j=0∑Mj−1I(x+i−ai,y+j−aj)K(i,j)
- H ( x , y ) H(x,y) H(x,y)为图像第x行、第y列像素,即目标像素,的计算结果;
- K ( i , j ) K(i,j) K(i,j)为卷积核第i行,第j列的系数;
- M i , M j M_i, M_j Mi,Mj分别为卷积核的总行数和总列数;
- a i , a j a_i, a_j ai,aj分别为卷积核中锚点的行数和列数;
- I ( x + i − a i , y + j − a j ) I(x+i-a_i, y+j-a_j) I(x+i−ai,y+j−aj)为目标像素的邻近像素。
虽然公式看上去有点复杂,但是好在OpenCV给我们提供了一个便利的API来实现线性滤波的算法。
API
在OpenCV中可以用filter2D()函数来实现线性滤波操作。其函数原型如下:
void cv::filter2D(InputArray src,
OutputArray dst,
int ddepth,
InputArray kernel,
Point anchor = Point(-1, -1),
double delta = 0,
int borderType = BORDER_DEFAULT)
src:输入图片dst:输出图片,与输入图片有相同的尺寸和颜色通道数ddepth:输出的数据格式,-1表示与原图保持同样的数据格式kernel:卷积核数组anchor:锚点坐标,默认为(-1, -1),即卷积核的中心delta:可选的偏移值borderType:图片边缘的扩充方式(由于卷积核的锚点无法覆盖图像边缘的像素,所以必须以某种方法扩充原图,使得锚点能够覆盖原有的边缘),默认为镜像扩充
实例
这里使用各种尺寸的归一化滤波作为例子。一个3*3的归一化滤波卷积核如下:
K
=
1
3
⋅
3
[
1
1
1
1
1
1
1
1
1
]
K=\frac{1}{3 \cdot 3} \begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{bmatrix}
K=3⋅31
111111111
使用著名的lena图片作为例子。
为了能够展示不同尺寸的卷积核带来的归一化滤波效果,这里使用了一个循环来进行迭代。在循环体内将卷积核的尺寸依次循环地设置为55, 77, 99, 1111, 13*13。具体代码如下:
#include <opencv2/imgproc.hpp>
#include <opencv2/imgcodecs.hpp>
#include <opencv2/highgui.hpp>
using namespace cv;
int main() {
Mat src{ imread("lena.jpg") };
Point anchor{ Point(-1, -1) }; //锚点为卷积核中心
double delta{ 0 }; //偏移值为0
int ddepth{ -1 }; //输出数据类型与原图一致
int ind{ 0 }, kernel_size;
Mat kernel, dst;
for (;;) {
kernel_size = 3 + 2 * (ind % 5); //卷积核的尺寸为5,7,9,11,13,不断循环
kernel = Mat::ones(kernel_size, kernel_size, CV_32F)
/ static_cast<float>(kernel_size * kernel_size); //创建归一化滤波的卷积核
//自定义滤波操作
filter2D(src,
dst,
ddepth,
kernel,
anchor,
delta,
BORDER_DEFAULT);
//显示结果图片
imshow("filter2D", dst);
char c = static_cast<char>(waitKey(500));
if (c == 27) //按ESC则退出
break;
ind++;
}
}
效果如下:
- 5*5的归一化滤波结果

- 7*7归一化滤波结果

- 9*9归一化滤波结果

- 11*11归一化滤波结果

- 13*13归一化滤波结果

可以看到卷积核越大,滤波后的图片越模糊。













![[io]进程间通信 -信号概念、分类、工作原理](https://i-blog.csdnimg.cn/direct/af0bf23852d942528a8295ca466be1eb.png)



