Abstract

从给定的基本矩阵中进行两个摄像头的自我校准问题是几何计算机视觉中的基本问题之一。在已知主点和正方形像素的假设下，Bougnoux公式提供了一种计算两个未知焦距的方法。然而，在许多实际情况下，由于常见的奇异性，公式会产生不准确的结果。此外，估算值对计算出的基本矩阵中的噪声和假定的主点位置非常敏感。因此，在本文中，我们提出了一种高效且鲁棒的迭代方法，用于估计给定基本矩阵和相机内参估计先验值的焦距和主点。此外，我们研究了一种计算效率高的RANSAC模型生成检查方法，该方法可以提高估计模型的准确性，同时减少总计算时间。对真实和合成数据的广泛实验表明，即使依赖不准确的先验值，我们的迭代方法在焦距估计的准确性方面也显著优于Bougnoux公式和其他先进方法。相关方法和实验的代码可在相机校准中找到，即相机内参估计问题，是计算机视觉中的一个基本问题，有许多应用。估计内参（如焦距和主点）的精度显著影响结构自运动（SfM）、视觉定位、3D物体检测、增强现实和其他应用的精度。经典校准方法使用已知校准图案（如棋盘格）或观察场景的额外知识来估计相机内参。因此，它们通常不切实际。相比之下，自校准方法不需要额外的场景几何知识，而依赖于图像特征的自动检测。因此，它们在许多应用中更可取。
代码地址：
https://github.com/kocurvik/robust_self_calibration

Introduction

在本文中，我们研究了两个摄像头的自校准问题，这两个摄像头可能具有不同的内参，捕捉同一个场景。两个摄像头的几何关系可以通过基本矩阵来描述。Bougnoux在1998年提出了一种方法，它假设主点已知且像素是正方形的，可以从基本矩阵中用封闭形式的公式得到焦距。这种方法很方便，因为通常主点被假定在图像中心。但Bougnoux公式和其他类似方法在估计焦距时容易受到误差的影响，有时甚至会产生不实际的虚数焦距。这是因为这些方法对基本矩阵中的噪声和主点位置的假设非常敏感。此外，当摄像头的主轴共面时，这些方法会失效，这种情况在拍摄同一对象的不同视角图像时很常见。

另一种迭代优化方法可以估计摄像头的焦距和主点，解决了一些上述问题，但仍然依赖于Bougnoux公式，在某些摄像头配置下可能不准确。我们提出的方法将估计焦距和主点的问题转化为一个约束优化问题，使用先验值，并确保解满足Kruppa方程。我们通过寻找拉格朗日函数的驻点来解决这个优化问题，这导致了一个复杂的多项式方程组，但我们通过迭代和Grobner基方法高效地求解它。每次迭代中，我们解决一个涉及两个变量的四次多项式方程组。

Method

我们将从给定的基本矩阵F估计焦距的问题，使用先验条件作为优化问题来表述。设F的奇异值分解为F = UDV⊤，其中U = [u1, u2, u3]和V = [v1, v2, v3]是正交矩阵，D = diag(σ1, σ2, 0)是对角矩阵，包含F的两个非零奇异值σ1和σ2。

设ω*i = KiK⊤i是第i个相机的绝对圆锥的对偶图像，i = 1, 2，Ki是3×3的校准矩阵，形式如下所示:

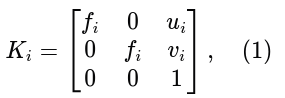
其中fi是焦距，主点ci = [ui, vi]⊤。对于固定主点，例如ci = [0, 0]，i = 1, 2，从给定的基本矩阵F中提取焦距有一个封闭形式的解决方案，即Bougnoux公式。由于这个公式可能导致不稳定或虚数估计，在本公式中，我们允许移动估计的主点以避免这种不稳定性。

对于非固定主点ci，F可以分解为本质矩阵E和两个形式如(1)的校准矩阵，有无限多种分解方式。因此，我们将从F估计焦距的问题表述为一个受约束的优化问题，在优化过程中，焦距以及两个图像中主点的位置都被优化以最小化代价函数：

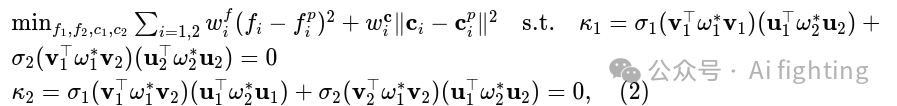
其中fpi和cpi = [upi, vpi]⊤，i = 1, 2是焦距和主点的先验值，wfi和wci是预定的权重，κ1 = 0和κ2 = 0是两个Kruppa方程，它们是焦距和主点的函数，出现在ω*i = KiK⊤i中。

Kruppa方程确保输入的基本矩阵F和估计的校准矩阵K1和K2（1），矩阵K⊤1FK2是一个有效的基本矩阵。

代价函数(2)代价函数有几个优点。(1)它不包含Sampson误差项，(2)它直接作用在焦距fi上，而不是焦距的平方f2i。(3)最小化(2)不需要使用Bougnoux公式[2]进行计算或初始化，这样的初始化可能与真实焦距相差很远，在许多情况下可能导致f2i ≤ 0。因此，最小化(2)不需要使用f2i ≤ 0的特殊惩罚项。

受约束的优化问题(2)可以使用拉格朗日乘数法转换为无约束问题。这导致拉格朗日函数L(f1, f2, c1, c2, λ1, λ2)：

其中λ1和λ2是拉格朗日乘数。常数“−2”是为了更方便地后续操作方程而引入的，不影响最终解决方案。

在这种情况下，如果(f⋆1, f⋆2, c⋆1, c⋆2)是原始受约束问题(2)的最小点，那么存在λ⋆1和λ⋆2，使得(f⋆1, f⋆2, c⋆1, c⋆2, λ⋆1, λ⋆2)是L(3)的静止点，即所有L的偏导数消失的点。拉格朗日函数L(f1, f2, c1, c2, λ1, λ2)(3)是一个八个未知数的函数。因此，为了找到L的所有静止点，我们需要解决以下八个多项式方程的系统：

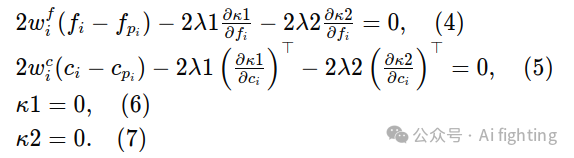
不幸的是，八个方程(4)-(7)的系统太复杂，无法使用代数方法有效解决，例如使用Grobner基方法。接下来，我们提出了一种迭代方法，有效地找到系统(4)-(7)的解，该解最小化了代价函数(2)。

1. 迭代方法

首先，让我们表示Δfi = fi − fp_i, Δci = ci − cp_i, i = 1, 2。从方程(4)-(5)我们有

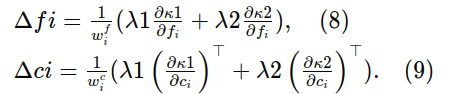
原始受约束优化问题(2)中的代价函数可以重写为

我们提出的迭代解方程(4)-(7)的方法遵循迭代三角测量方法的思想。首先，让我们用sk−1 = 〈f k−1 1, f k−1 2, c k−1 1, c k−1 2〉表示在(k − 1)次迭代后焦距和主点的最佳当前估计。先前值f0i ≡ fpi, c0i ≡ cpi, i = 1, 2用作初始化。在第k次迭代中，通过用当前最佳估计sk−1 = 〈f k−1 1, f k−1 2, c k−1 1, c k−1 2〉替换方程(8)-(9)右侧的焦距和主点〈f1, f2, c1, c2〉来获得更新的估计sk = 〈f k 1, f k 2, c k 1, c k 2〉。通过这种方式，我们得到Δfi和Δci的表达式，它们是两个拉格朗日乘数λ1和λ2的函数。然后，将Δfi和Δci依次代入Kruppa方程(6)和(7)。这是通过使用关系fi = Δfi + fpi和ci = Δci + cpi将Δfi和Δci，i = 1, 2代入ω*i来完成的。

更新后的Kruppa方程(6)和(7)，我们表示为κk1 = 0和κk2 = 0，形成一个由两个未知数构成的四次方程组。这个系统最多有16个实数解，可以使用Grobner基方法有效解决。最终求解器执行一个20×36矩阵的消元，并从16×16矩阵的特征值和特征向量中提取解。从多达16个可能的解中，选择一个使|λ1| + |λ2|最小的解λk1和λk2。这个解用于使用方程(8)-(9)计算第k次迭代的更新Δfki和Δcki，然后是新的焦距和主点的估计sk = 〈f k 1, f k 2, c k 1, c k 2〉。

迭代算法在连续两次迭代的误差相对变化|ek−ek−1|/ek < ε，对于给定的阈值ε时停止。注意，在每次迭代中，获得的解满足Kruppa方程κ1 = 0和κ2 = 0。这意味着对于输入的基本矩阵F和估计的校准矩阵K1和K2(1)，矩阵K⊤1FK2在每次迭代中都是一个有效的基本矩阵。

f1 = f2的情况可以使用相同的方法解决。在这种情况下，在代价函数(2)中，以及在拉格朗日函数和(4)-(5)中，我们只有i = 1。然而，由于我们仍然有两个Kruppa方程κ1 = 0和κ2 = 0，最终算法也依赖于解决两个未知数的四次方程组的解。算法总结在补充材料中。

2. RANSAC中的实焦距检查

在1中提出的方法通常应用于使用鲁棒的RANSAC风格估计获得的基本矩阵F。与Bougnoux公式相比，我们的方法在存在噪声或主点位置错误的情况下不会出现虚数焦距估计。因此，我们的方法不需要检查RANSAC返回的基本矩阵是否可以分解为实数焦距。尽管如此，正如我们在实验中观察到的，当使用Bougnoux公式分解时，导致虚数焦距的基本矩阵通常不提供良好的估计，因此不会被RANSAC选为最佳模型。

受到这一观察的启发，我们提出了一个基于拒绝导致虚数焦距的模型的RANSAC的简单修改。拒绝是在对所有点对应关系进行模型评分之前完成的。这减少了评分模型所需的计算时间，这种模型不太可能导致最终输出。因此，这种方法类似于其他退化检查算法。

为了拒绝模型，Bougnoux公式的修改版本，它的形式是基本矩阵元素的两个多项式的比率。公式返回平方焦距。当平方焦距之一的符号为负时，我们拒绝该模型。这种方法不需要使用SVD或其他昂贵的矩阵操作。这种检查可以实施到RANSAC的不同变体中，并且正如我们稍后在实验中所示，它导致计算时间减少，同时保持甚至提高姿态估计的准确性。实现细节可以在补充材料(SM)中找到。

Experiment

仿真实验：

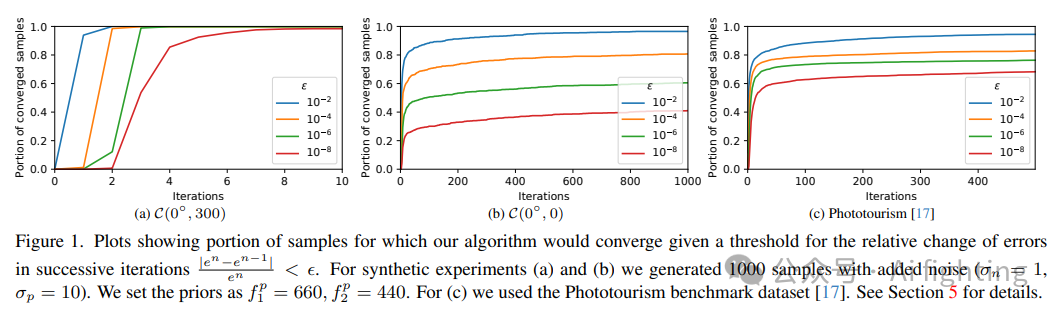
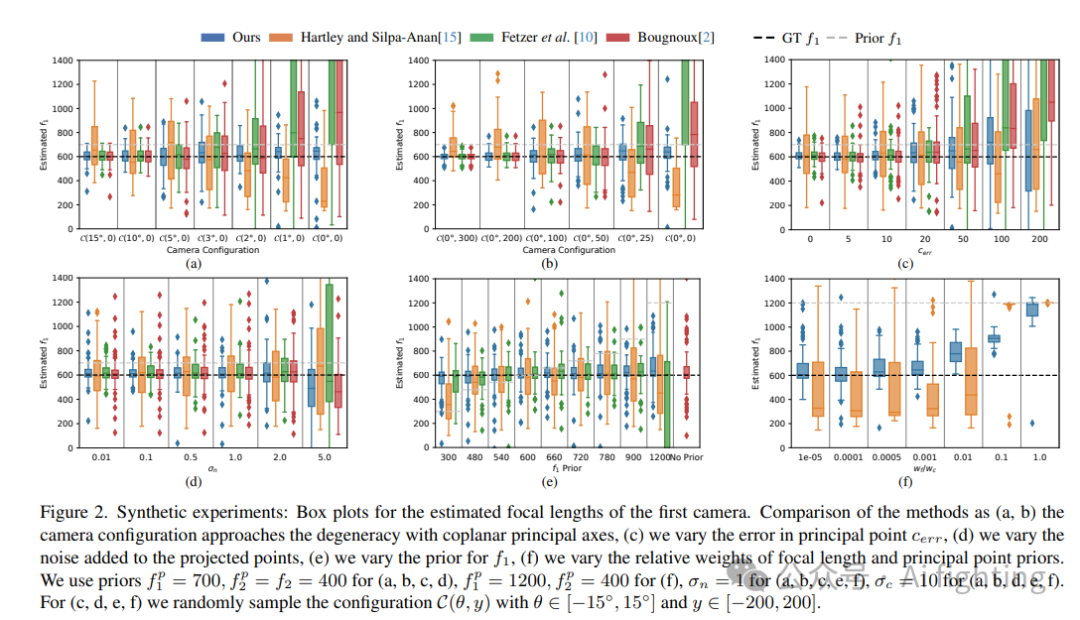
真实实验：

度量标准：
我们采用平均平均精度（mAA）指标。这个指标的基础是姿态误差（perr），它是旋转和平移误差中的最大值，以度为单位计算。

基本矩阵估计：我们使用LoFTR获得点对应关系。我们在大小调整为最大尺寸等于1024像素的图像上进行推理。为了估计基本矩阵，我们使用MAGSAC++[1]，并将极线阈值设置为3像素。

我们还进行了有无使用3.2小节中描述的实际焦距检查（RFC）的实验。图3显示，在Phototourism数据集上，使用RFC获得的基本矩阵通常可以导致更准确的姿态估计，同时也可以减少各种RANSAC实现的计算时间。

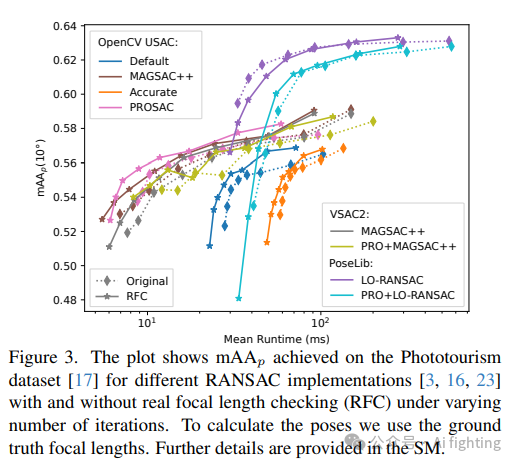
比较方法：
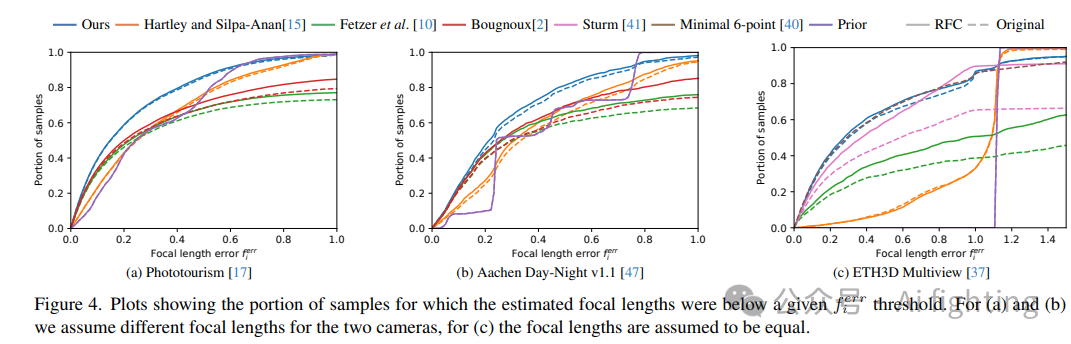
我们将我们的方法与三种最先进的方法进行比较。我们评估了Bougnoux公式、Hartley和Silpa-Anan的迭代方法以及Fetzer等人的迭代方法。

对于所有图像，我们考虑主点位于它们的中心，这是一个常用的假设。除了Bougnoux公式之外，所有方法都需要焦距的先验或初始估计。按照COLMAP中建立的常规做法，我们将焦距的先验初始化为图像最大尺寸的1.2倍。这种初始设置意味着相机大约有50度的视野。

结果：
表1中报告了姿态和焦距的中位数误差和平均平均精度分数。在两个数据集上，我们的方法在估计焦距的准确性方面显著优于其他方法。我们方法在焦距准确性方面的优越性也可以在图4a和4b中看到。在姿态准确性方面，我们的方法也比所有比较的方法提供了更准确的结果。

结果还表明，在RANSAC中执行3.2小节提出的实际焦距的RFC通常可以在比较的方法中提高姿态和焦距的准确性。

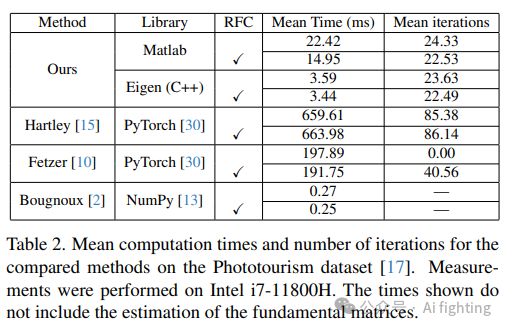
计算速度：
表2显示了各种方法的平均计算时间。我们的方法比其他迭代方法显著更快。请注意，我们方法的实现尚未优化，仍有加速的空间。

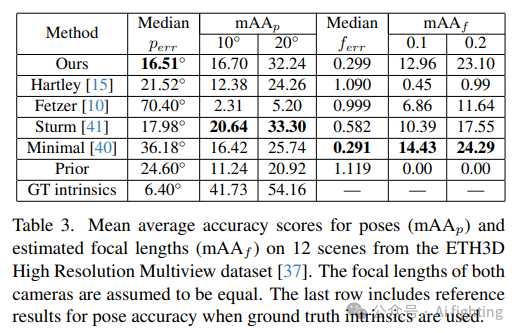
相等的焦距：
我们还评估了我们的方法在假定两个焦距相等的情况下的表现。在这种情况下，我们使用第3.1节中我们迭代算法的修改版本。为了进行评估，我们使用了ETH3D Multiview数据集。我们使用测试集中12个场景的所有满足共视性标准的图像对，总共得到3830对。

总结：

文章的主要贡献如下：

1. 提出了一种新颖的迭代方法，用于从基本矩阵中估计焦距和主点。该方法在合成数据和真实大规模数据集上经过评估，显示出在焦距估计和相机姿态准确性方面具有显著的性能优势。

2. 介绍了一种在RANSAC算法中用于检测和排除导致虚焦距的基本矩阵的高效退化检查方法。实验结果表明，这种方法能够在不同的RANSAC变体中提高计算速度，并提升姿态和焦距估计的准确性。

引用文章：

Kocur_Robust_Self-calibration_of_Focal_Lengths_from_the_Fundamental_Matrix

关注我的公众号auto_driver_ai(Ai fighting), 第一时间获取更新内容。