第57天,图论07,两个最小生成树算法的讲解💪(ง •_•)ง💪,编程语言:C++
目录
题目:53. 寻宝(第七期模拟笔试) (kamacoder.com)
prim算法精讲
拓展
总结:
kruskal算法精讲
拓展
总结
题目:53. 寻宝(第七期模拟笔试) (kamacoder.com)


本题是标准的最小生成树的题目。生成树是指包含图的全部顶点的一个极小连通子图。而最小生成树,就是在图的边有权值的情况下,权值相加和最小的生成树。(最小生成树的边是顶点数 - 1;最小生成树可能有多个,但边的权值之和总是唯一且最小的)
以本题的示例为例,有7个顶点,因此我们应该找到 7 - 1 = 6 条边把这7个点连接在一起,并使得所得的权值是最小的。

解决最小生成树问题的方法主要有两种:1.Prim算法;2.Kruskal算法
prim算法精讲
文档讲解:代码随想录prim算法精讲
prim算法采用了贪心的策略,从一个节点出发,每次寻找距离最小的节点,并逐渐加入最小生成树当中。
prim算法的核心三步,也称之为prim三部曲:
- 第一步,选距离生成树最近节点(距离值最小)
- 第二步,最近节点加入生成树
- 第三步,更新非生成树节点到生成树的距离(即更新minDist数组)
minDist数组用来记录每一个节点距离最小生成树的最近距离。 理解这一点非常重要,这也是 prim算法最核心要点所在。
1. 初始状态:minDist数组里的数值初始化为最大数,因为本题 节点距离不会超过10000,所以 初始化最大数为 10001就可以。这是默认每个节点距离最小生成树是最大的,这样后面我们才便于更新。

2.开始构造最小生成树:一句prim三部曲进行分析
① 第一步,选距离生成树最近节点:选择距离最小生成树最近的节点,加入到最小生成树,刚开始还没有最小生成树,所以随便选一个节点加入就好。(因为最后每个节点都会到最小生成树里面)
② 第二步,最近节点加入生成树:假设节点1已经是最小生成树里面的节点了。
③第三步,更新非生成树节点到生成树的距离,也就是更新minDist数组:我们通过遍历生成树中的节点,然得到非生成树到节点的距离。例如通过节点1我们知道:节点2 与 节点1 的距离为1,比原先的 距离值10001小,所以更新minDist[2];节点3 和 节点1 的距离为1,比原先的 距离值10001小,所以更新minDist[3];节点5 和 节点1 的距离为2,比原先的 距离值10001小,所以更新minDist[5]。最后可以得到:

同时需要标记minDist数组里更新的权值,是哪两个节点之间的权值,例如 minDist[2] =1 ,这个 1 是 节点1 与 节点2 之间的连线,清楚这一点对最后我们记录最小生成树的权值总和很重要。
3.进行prim三部曲循环:
① 第一步,选距离生成树最近节点:选取一个距离最小生成树(节点1)最近的非生成树里的节点,节点2,3,5 距离 最小生成树(节点1)最近,选节点 2(其实选节点3或者节点2都可以,距离一样的)加入最小生成树。
② 第二步,最近节点加入生成树:此时节点1 和节点2,已经算最小生成树的节点。
③第三步,更新非生成树节点到生成树的距离,也就是更新minDist数组:
- 节点3 和 节点2 的距离为2,和原先的距离值1 小,所以不用更新。
- 节点4 和 节点2 的距离为2,比原先的距离值10001小,所以更新minDist[4]。
- 节点5 和 节点2 的距离为10001(不连接),所以不用更新。
- 节点6 和 节点2 的距离为1,比原先的距离值10001小,所以更新minDist[6]。
之后不断重复这个过程,最后我们就可以得到:

最后得到了一个最小生成树,绿色的边将所有节点链接到一起,并且保证权值是最小的,因为我们满足在更新minDist数组的时候,都是选距离最小生成树最近的点加入到树中。最后我们要求最小生成树里边的权值总和,就是把最后的minD
最后根据以上的过程,我们可以写出代码:
#include <iostream>
#include <vector>
#include <climits> //这个头文件包含了各种类型的最大值和最小值,例如:INT_MAX
using namespace std;
int main() {
int v, e;
cin >> v >> e;
//采用邻接表的方式保存图,一般空位置我们会选择0来作为权值,
//但本题由于我们需要比较出最小值,因此空位置我们选取10001便于进行遍历
int s, t, k;
vector<vector<int>> grid(v + 1, vector<int>(v + 1, 10001));
while(e--) {
cin >> s >> t >> k;
//因为是无向图,两边都得给予赋值
grid[s][t] = k; // k 为权值
grid[t][s] = k;
}
vector<int> minDist(v + 1, 10001); //minDist数组,记录每个节点到最小生成树的距离
vector<bool> isInTree(v + 1, false); //记录当前点是否在最小生成树内
for(int i = 1; i < v; i++) { //注意要从节点1开始,且只需要遍历V-1次就能覆盖所有节点,加上v的话,最后一次是多余的不会改变minDist里面的值
//1.prim第一步,选取距离生成树最近的点
int cur = 0; //确定选取的点
int maxDist = INT_MAX; //记录当前距离的最小值
for(int j = 1; j <= v; j++) {
if(!isInTree[j] && minDist[j] < maxDist) { //如果当前点没有加入最小生成树,且距离最近
cur = j;
maxDist = minDist[j];
}
}
//2.prim第二步,将节点加入到最小生成树当中
isInTree[cur] = true;
//3.prim第三步,依据节点cur,更新minDist数组
for(int k = 1; k <= v; k++) {
if(!isInTree[k] && grid[cur][k] < minDist[k]) { //这里要注意,已经加入了最小生成树的点,就不能更改下标值了
minDist[k] = grid[cur][k];
}
}
}
//统计结果,统计minDist数组
int result = 0;
for(int i = 2; i <= v; i++) { //不记录节点1,因为根据我们的代码逻辑,第一个选择的点是节点1,且节点1下面的权值是没有改过的,是10001
result += minDist[i];
}
cout << result << endl;
return 0;
}拓展
上面我们求出了最小生成树边的权值之和。但如果需要我们打印出最小生成树的每条边,或者要把这个最小生成树画出来,应该怎么做。
显然我们需要把最小生成树的每条边记录下来。那我们就需要解决两个问题:1.使用什么结构来记录边;2.如果进行边的记录。
对于第一个问题,我们只需要记录两个节点即可,两个节点连成一条边。因此我们可以采用一维数组进行纪录,parent[节点编号] = 节点编号,这样就把一条边记录下来,假如节点非常多,编号很大,也可以考虑使用map进行记录。
我们使用一维数组记录其实有向边,但这里我们不需要关注对向
vector<int> parent(v + 1, -1);接下来就是对于第二个问题的办法。依据prim算法三部曲,我们可以发现,我们只有在第三步更新了minDist数组,也就是说在第三步我们才去更新了边的权值,因此我们也可以在这一步更新parent数组。
for (int j = 1; j <= v; j++) {
if (!isInTree[j] && grid[cur][j] < minDist[j]) {
minDist[j] = grid[cur][j];
parent[j] = cur; // 记录最小生成树的边 (注意数组指向的顺序很重要)
}
}注意这个地方代码的指向非常重要,是parent[j] = cur,而不是parent[cur] = j,因为cur是已经确定加入了最小生成树的点,同时我们是依据cur进行节点的遍历的,我们更新的边的权值,也是非最小生成树的点到最小生成树的距离,而不是找cur到它们的最小距离。如果这样运行下去只会不断更改parent[cur]的值而已,最后也只表示了cur和最后一个节点相连,和我们的需求是违背的。
当然我们也可以采用二维数组来记录,那么就不会出现上述情况了, ,例如 parent[节点编号A][节点编号B] = 1 ,parent[节点编号B][节点编号A] = 1,来表示 节点A与 节点B相连,这么做的话,就是多开辟的内存空间。
#include<iostream>
#include<vector>
#include <climits>
using namespace std;
int main() {
int v, e;
int x, y, k;
cin >> v >> e;
vector<vector<int>> grid(v + 1, vector<int>(v + 1, 10001));
while (e--) {
cin >> x >> y >> k;
grid[x][y] = k;
grid[y][x] = k;
}
vector<int> minDist(v + 1, 10001);
vector<bool> isInTree(v + 1, false);
//加上初始化
vector<int> parent(v + 1, -1);
for (int i = 1; i < v; i++) {
int cur = -1;
int minVal = INT_MAX;
for (int j = 1; j <= v; j++) {
if (!isInTree[j] && minDist[j] < minVal) {
minVal = minDist[j];
cur = j;
}
}
isInTree[cur] = true;
for (int j = 1; j <= v; j++) {
if (!isInTree[j] && grid[cur][j] < minDist[j]) {
minDist[j] = grid[cur][j];
parent[j] = cur; // 记录边
}
}
}
// 输出 最小生成树边的链接情况
for (int i = 1; i <= v; i++) {
cout << i << "->" << parent[i] << endl;
}
}
//运行结果
1->-1
2->1
3->1
4->3
5->4
6->2
7->5 
总结:
我们首先需要牢记prim算法三部曲:
- 第一步,选距离生成树最近节点
- 第二步,最近节点加入生成树
- 第三步,更新非生成树节点到生成树的距离(即更新minDist数组)
这是prim算法的主要框架。其次要明白minDist数组是prim算法的灵魂,它帮助prim算法完成最重要的一步,就是找到距离最小生成树最近的点。
同时我们还拓展了parent数组,来记录最小生成树的每一条边!!并且,因为使用一维数组,数组的下标和数组如何赋值很重要,一定不要搞反,导致结果被覆盖。
kruskal算法精讲
文档讲解:代码随想录kruskal算法精讲
接下来我们来了解解决最小生成树的第二种算法kruskal算法。
与prim算法从节点出发相比,kruskal算法同样采用了贪心算法的逻辑,它的贪心逻辑是每次选取权值最小的边,属于是从边出发的算法。(prim 算法是维护节点的集合,而 Kruskal 是维护边的集合)
kruskal的思路:
- 将边的权值排序,因为要优先选最小的边加入到生成树里
- 遍历排序后的边:①如果边首尾的两个节点在同一个集合,说明如果连上这条边图中会出现环。②如果边首尾的两个节点不在同一个集合,加入到最小生成树,并把两个节点加入同一个集合。
依据上述逻辑,我们以示例为例查看解题过程:

将边按权值小到大进行排列,排列后的顺序应该为: [(1,2) (4,5) (1,3) (2,6) (3,4) (6,7) (5,7) (1,5) (3,2) (2,4) (5,6)]。权值相同的边,先后顺序对解题结果没有影响。
开始从头遍历排序后的边:
选边(1,2),节点1 和 节点2 不在同一个集合,所以生成树可以添加边(1,2),并将节点1,节点2放在同一个集合。

选边(4,5),节点4和节点 5 不在同一个集合,生成树可以添加边(4,5) ,并将节点4,节点5放到同一个集合。

选边(1,3),节点1 和 节点3 不在同一个集合,生成树添加边(1,3),并将节点1,节点3 放到同一个集合。

选边(2,6),节点2 和 节点6 不在同一个集合,生成树添加边(2,6),并将节点2,节点6 放到同一个集合。

选边(3,4),节点3 和 节点4 不在同一个集合,生成树添加边(3,4),并将节点3,节点4 放到同一个集合。
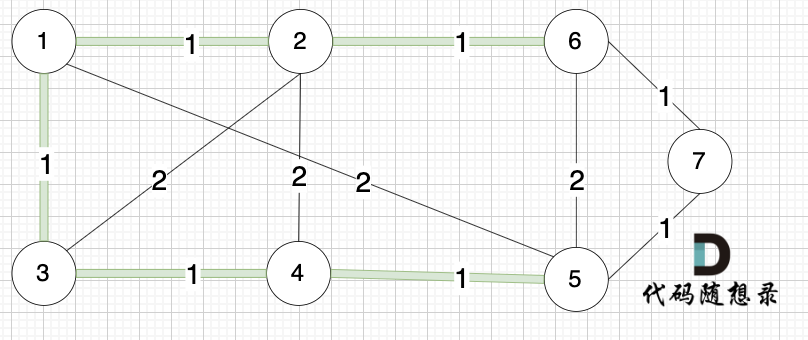
选边(6,7),节点6 和 节点7 不在同一个集合,生成树添加边(6,7),并将 节点6,节点7 放到同一个集合。
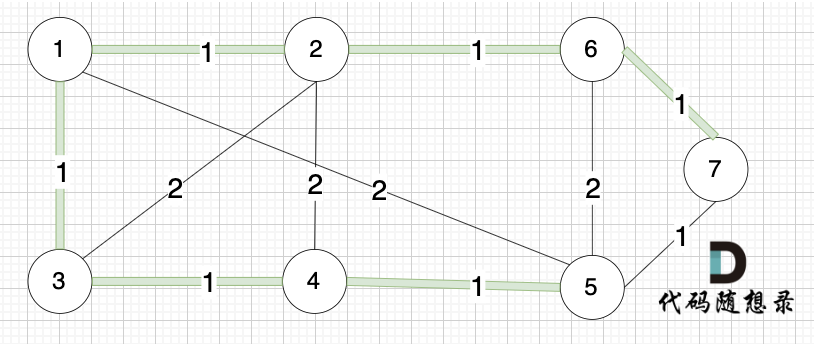
接着应该是选边(5,7),但发现5,7在同一个集合,不做计算。然后选边(1,5)两个节点也在同一个集合,不做计算,后面的边也均是如此。最后我们就得到了一个最小生成树。
显然在这个过程中,我们最重要的两个部分就是:1.判断两个节点是否在同一个集合;2.将两个节点加入到一个集合当中。
这就需要我们使用之前的知识并查集来辅助求解。回顾一下,并查集的主要功能就是:将两个元素添加到一个集合中,判断两个元素在不在同一个集合。
最后我们可以得到求解的代码:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// l,r为 边两边的节点,val为边的数值
struct Edge { //使用到结构体来保存边和边的权值
int l, r, val;
};
// 节点数量
int n = 10001;
// 并查集标记节点关系的数组
vector<int> father(n, -1); // 节点编号是从1开始的,n要大一些
// 并查集初始化
void init() {
for (int i = 0; i < n; ++i) {
father[i] = i;
}
}
// 并查集的查找操作
int find(int u) {
return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
}
// 并查集的加入集合
void join(int u, int v) {
u = find(u); // 寻找u的根
v = find(v); // 寻找v的根
if (u == v) return ; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回
father[v] = u;
}
int main() {
int v, e;
int v1, v2, val;
vector<Edge> edges;
int result_val = 0;
cin >> v >> e;
while (e--) {
cin >> v1 >> v2 >> val;
edges.push_back({v1, v2, val});
}
// 执行Kruskal算法
// 按边的权值对边进行从小到大排序
sort(edges.begin(), edges.end(), [](const Edge& a, const Edge& b) { //这是c++的一种特殊的函数使用方式
return a.val < b.val;
});
// 并查集初始化
init();
// 从头开始遍历边
for (Edge edge : edges) {
// 并查集,搜出两个节点的祖先
int x = find(edge.l);
int y = find(edge.r);
// 如果祖先不同,则不在同一个集合
if (x != y) {
result_val += edge.val; // 这条边可以作为生成树的边
join(x, y); // 两个节点加入到同一个集合
}
}
cout << result_val << endl;
return 0;
}拓展
同理,如果题目要求把边输出,我们应该怎么操作。
由于kurskal算法,本身就是对边进行操作的算法,因此边的结构是很清晰的,我们只需要把我们加入了最小生成树的边记录下来就可以了。
也就是在最后一步,判断两个节点不在同一个集合的时候,这两个节点的边就加入到最小生成树。
vector<Edge> result; // 存储最小生成树的边
// 如果祖先不同,则不在同一个集合
if (x != y) {
result.push_back(edge); // 记录最小生成树的边
result_val += edge.val; // 这条边可以作为生成树的边
join(x, y); // 两个节点加入到同一个集合
}最后我们再打印输出:
// 打印最小生成树的边
for (Edge edge : result) {
cout << edge.l << " - " << edge.r << " : " << edge.val << endl;
}
//输出结果
1 - 2 : 1
1 - 3 : 1
2 - 6 : 1
3 - 4 : 1
4 - 5 : 1
5 - 7 : 1总结
了解了两种解决最小生成树的方法prim算法和kruskal算法。那么在我们使用的时候如何选择这两种算法呢。
这两种算法的关键区别在于,prim维护的是节点的集合,kruskal维护的是边的集合。一个是对节点进行遍历,一个是对边进行遍历。因此我们可以得出结论如果 一个图中,节点多,但边相对较少,那么使用Kruskal 更优。反之对于边稠密的图则使用prim算法更好。
总结就是:
- 边稠密的图,选择prim算法更好
- 边稀疏的图,选择kruskal算法更好
Prim 算法 时间复杂度为 O(n^2),其中 n 为节点数量,它的运行效率和图中边树无关。
Kruskal算法 时间复杂度 为 nlogn,其中n 为边的数量。