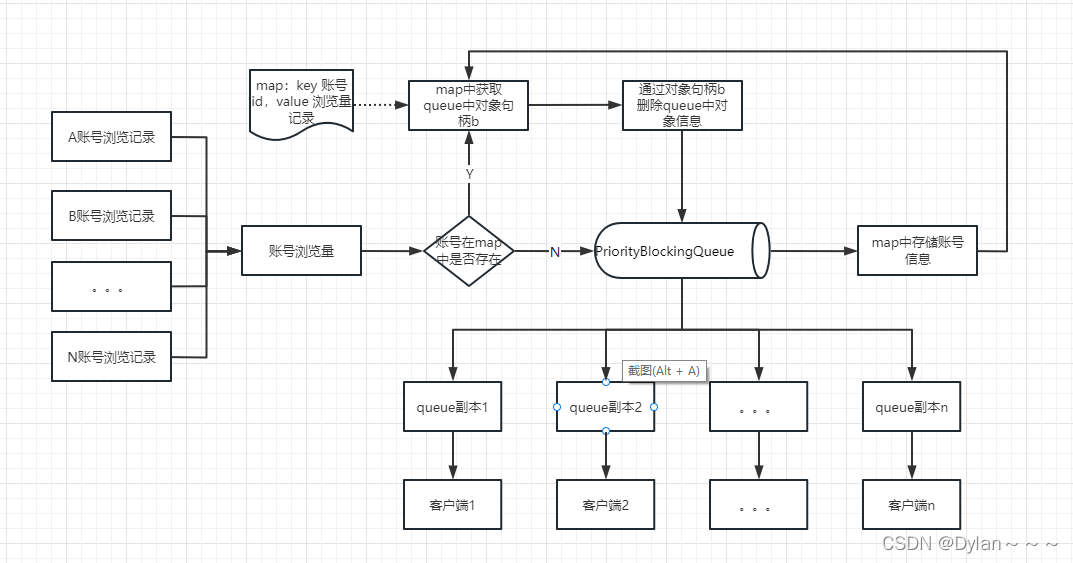
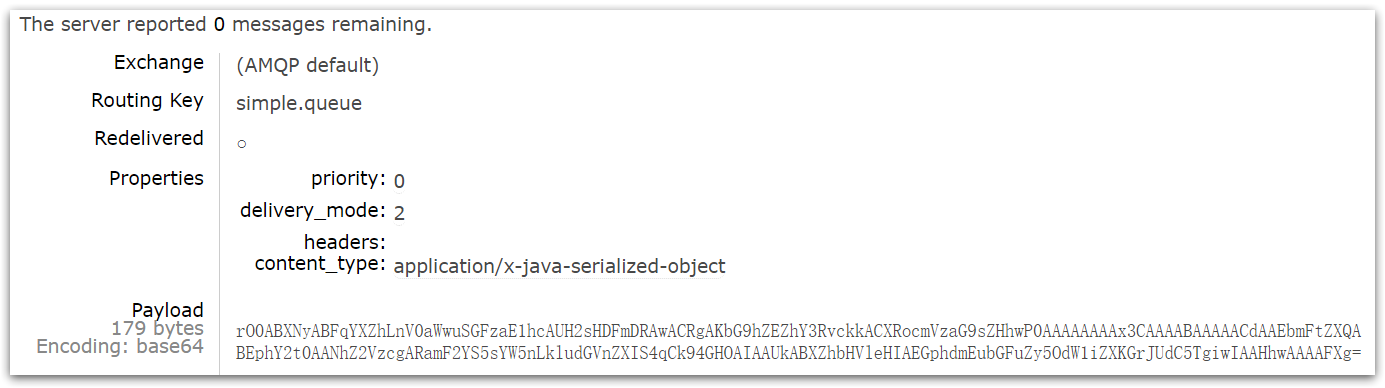
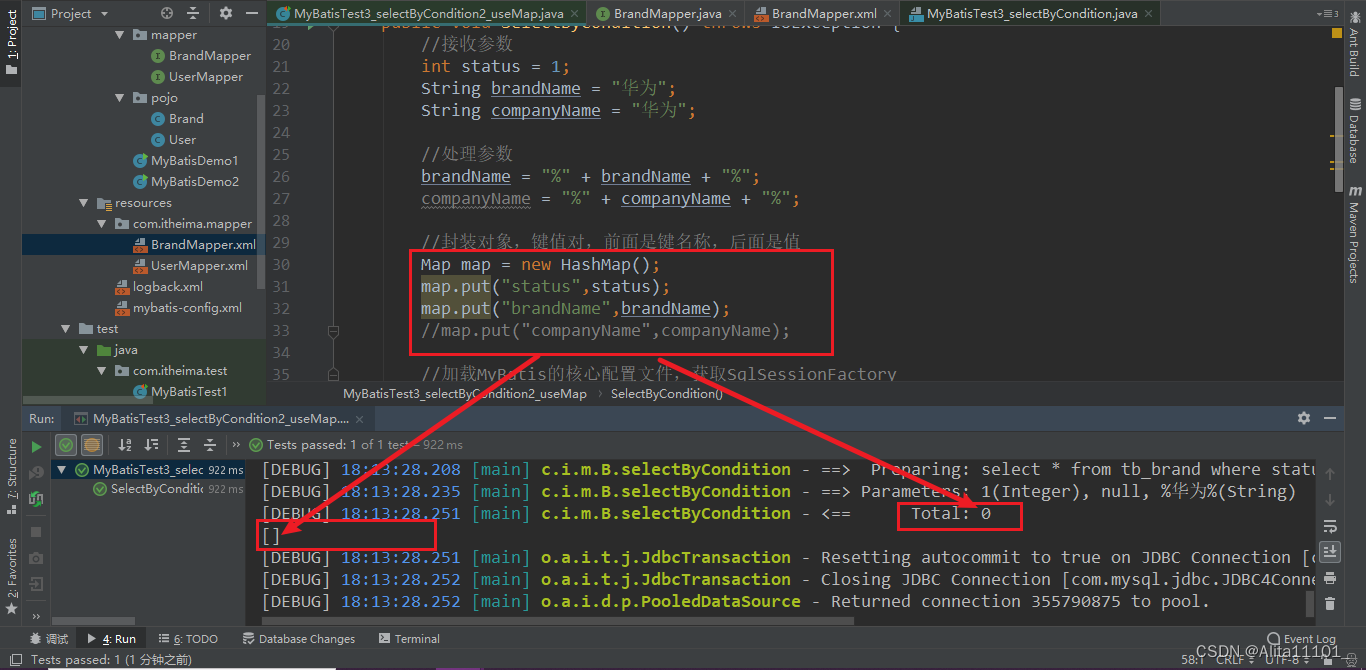
SDU 线性代数 - 期末复习(无二次型部分)
- 第一章: 矩阵
- 1. 矩阵概念
- 2. 矩阵运算
- 💙1)线性运算:
- 1》加、减法:
- 2》数乘
- 💙2)乘法运算
- 💙3)矩阵的转置
- 3. 方阵 的行列式及其运算
- 4.余子式、代数余子式
- 5.伴随矩阵(必须是方阵)
- 6.克拉默法则
- 7.初等变换
- 8.等价和等价类
- 9.标准型 (不一定方)
- 10.秩
- 11.逆矩阵(必须是方阵)
第一章: 矩阵
1. 矩阵概念
-
矩阵定义:由m×n个数aij(i = 1,2 ···,m ;j = 1,2 ···,n)按一定顺序排成的m行n列的矩形数表

注意:矩阵表示的是一个数表,不是一个具体的数 -
主对角线:
当m = n,即矩阵的行数与列数相同时,称矩阵为n阶方阵 或 n阶矩阵,在n阶方阵A中,元素aii (i = 1,2,···,n)排成的对角线称为方阵A的主对角线 -
行矩阵:
当m = 1时,得到一个1行n列的矩阵
A1×n = (a11 a12 ··· a1n)
称它为行矩阵 -
列矩阵:
当n = 1时,得到一个m行1列的矩阵
Am×1 = (a11 a21 ··· am1)T
称它为行矩阵
几种特殊矩阵↓
1) 零矩阵:
💛所有元素皆为0的矩阵称为零矩阵,简称零阵,记为O或Om×n
2) 对角矩阵(是方阵)
💛一个n阶方阵,若除主对角线上的元素aii (i = 1,2,···,n)外,其余元素全部为0,则称这个矩阵为对角矩阵,对角矩阵通常用Λ表示
(非主对角线上的零元素可省略不写) 也可记作:diag(λ1,λ2,···,λn)
也可记作:diag(λ1,λ2,···,λn)
3) 单位矩阵(是方阵)
💛是特殊的对角矩阵;
主对角线上元素全是1的对角矩阵称为单位矩阵,n阶单位矩阵通常用En(或I n)表示,下标n表示单位矩阵的阶数,有时也简记为E(或 I)

4) 标量矩阵(是方阵)
(又叫做“纯量矩阵”,“数量矩阵”)
💛主对角线上的元素全为常数k的对角矩阵称为标量矩阵
5) 三角形矩阵:(是方阵)
💛主对角线下(上)面的元素全为0的方阵称为上(下)三角形矩阵;上、下三角形矩阵统称为三角形矩阵
6) 阶梯型矩阵(不一定是方阵)
💛设A = (aij)m×n为非零矩阵,若非零行(至少有一个非零元素的行)全在零行的前面,且A中各非零行第一个(最后一个)非零元素前(后)面零元素的个数随行数增加而增加(减少),则称A为上(下)阶梯型矩阵
上阶梯型矩阵👇
下阶梯型矩阵则是0元素在右上↗方
 注意:阶梯型是以主对角线为“界限”像下面这样的矩阵就不是阶梯型
注意:阶梯型是以主对角线为“界限”像下面这样的矩阵就不是阶梯型

2. 矩阵运算
主要包括矩阵的线性运算、乘法运算、矩阵的转置
💙1)线性运算:
矩阵的加、减法、数乘运算统称为线性运算
1》加、减法:
同型矩阵A = (aij)m×n 与 B = (bij)m×n,称矩阵C = (cij)m×n = (aij±bij)m×n为矩阵A与B的和(差),记为C = A ± B
注意:只有同型矩阵才能相加(减),其和(差)矩阵仍是与它们同型的矩阵
性质:
(1)A+B = B+A
(2)(A+B)+C = A+(B+C)
(3)A+O = O+A = A
(4)A+(-A) = (-A)+A = O
2》数乘
矩阵A = (aij)m×n,k为常数,以k乘A的每一个元素得到的矩阵称为数k与矩阵A的数量乘积,简称数乘,记作kA,即kA = (k·aij)m×n
性质:
(1)k(A+B) = kA + kB
(2)(k+l) A=kA + lA
(3)(kl) A = k(lA)
(4)1A = A;( -1 )A = -A;0A = O
💙2)乘法运算
设A为m×p的矩阵,B为p×n的矩阵,那么称m×n的矩阵C为矩阵A与B的乘积,记作C = AB,其中矩阵C中的第i行第j列元素可以表示为: (AB)ij = cij = ai1b1j + ai2b2j + ······ + aipbpj
矩阵相乘的前提:左乘矩阵的列数 = 右乘矩阵的行数
注意:
(1) AB有意义,BA 不一定有意义
(2)一般来说AB ≠ BA,即矩阵乘法不满足交换律
(3)由AB = O不能推出A = O或B = O,即两个非零矩阵的 乘积可以是零矩阵
(4)由AB = AC 且A ≠ O,不能推出 B = C ,即矩阵乘法不满足消去律
性质:
(1) (AB)C = A(BC)
(2)A ( B+C ) = AB +AC
(3)( B+C ) A = BA + CA
(4)k (AB) = (kA) B = A (kB)
(5)Em Am×n = Am×nEn = Am×n
(6)Am×nOn×s = Om×s
💙3)矩阵的转置
将矩阵A = (aij)m×n的行列互换得到的矩阵称为矩阵A的转置矩阵,记作AT
 性质:
性质:
(1) (AT)T = A
(2)(A + B)T = AT +BT
(3)(kA)T = kAT(k是常数)
(4)⭐(AB)T = BTAT
性质(4)可以推广:(A1A2 ··· Am)T = AmT···A2TA1T
📘对称矩阵与反对称矩阵
设A为n阶方阵,若AT = A ,则称A为对称矩阵;若AT = - A,则称A为反对称矩阵
对称矩阵特点:aij = aji
反对称矩阵特点:aij = -aji ; 由此可推得 aii = 0(主对角线元素为0)
对于任意n阶方阵A,A+AT、AAT、ATA都是对称矩阵;而A - AT是反对称矩阵
任意方阵A都可以写成对称矩阵与反对称矩阵的和:
A = (A+AT)/2 + (A - AT)/2
注意:对称矩阵的乘积不一定是对称矩阵
可以证明:若A、B为同型对称矩阵,AB为对称矩阵⇔AB = BA
(充分:∵(AB)T = AB;∵(AB)T = BTAT = BA;∴AB = BA 必要:∵AB = BA;∵(AB)T = BTAT = BA;∴(AB)T = AB)
3. 方阵 的行列式及其运算
注意:必须是方阵才有行列式→行列式必须是“方的”
性质:
(1)上 / 下三角形行列式展开:主对角元素相乘
(2)互换两行(列),行列式变号
(3)行(列)的公因子可以提到行列式外面:
一个数 × 行列式 = 该数 × 行列式的某一行(列)
(4)(行列式的值为0:)①有零行(列)②某两行 (列)对应成比例
(5)⭐行列式中某一行(列)元素与零一行(列)对应元素的代数余子式的乘积 之和为0
(6) 若行列式中某一行(列)的所有元素都是两个数的和,则此行列式可以写成两个行列式的和
(7)奇数阶反对称行列式的值为0
运算性质:
(1) | kA | = kn| A |
(2)| AB | = | A | | B |
(3)| AT | = | A |
(2)的推广:①| ABCD··· | = | A | | B | | C | | D |···
②| Ak | = | A |k
4.余子式、代数余子式

注意推论↓*

5.伴随矩阵(必须是方阵)
“按行求,按列放”
性质:
(1)AA* = A*A = | A | E
(2) | A |A-1 = A*
(3)| A* | = | A | n-1

6.克拉默法则
n元1次方程组的系数行列式 D ≠ 0 ⇔ 有唯一解
⭐齐次:
D ≠ 0 → 仅有零解
D = 0 →有非零解
⭐非齐次:
D ≠ 0 → 有唯一解
D = 0 →无解 or 多解
7.初等变换

8.等价和等价类
等价:将矩阵A进行有限次的初等变换得到矩阵B,称A与B等价(注意不是相等),记作 A ≌ B 或 A ↔ B
等价类:所有与A等价的矩阵的集合称为一个等价类;
标准型是这个等价类中形状最简单的矩阵
9.标准型 (不一定方)
特点:左上角是一个单位矩阵,其余元素为0
一个矩阵的标准型唯一
决定因素:①原矩阵的行数、列数 ②上阶梯型非零行的行数
10.秩
“非零子式的最高阶数”
Am×n, 0 ≤ r(A) ≤ min{ m,n }
行满秩和列满秩:若 r(A) = m →行满秩;若 r(A) = n →列满秩
满秩和降秩:若r(A) = min{ m,n } →满秩;若r(A) < min{ m,n } →降秩
性质:
①方阵A满秩⇔ r(A) = n ⇔ | A | ≠ 0 ⇔ A可逆 ⇔ A非奇异 ⇔ A ≌ En
② r(AT) = r(A)
③A ≌ B ⇔ r(A) = r(B)
④P,Q满秩 ⇔ r(PAQ) = r(A) = r(PA) = r(AQ)
⑤矩阵A乘满秩矩阵X,AX的秩 = A的秩
⑥满秩矩阵的标准型为同阶单位矩阵
11.逆矩阵(必须是方阵)
AB = BA = E,A(B)是可逆矩阵,B(A)称为A(B)的逆矩阵
逆矩阵求法:初等变换法
 性质:
性质:
(1)若A可逆,(A-1)-1 = A、 | A-1 | = | A |-1 、(A-1)T =(AT)-1
(2)若AB同型且可逆,则AB可逆 (AB)-1 = B-1A-1
(3)若A可逆且常数k≠0,(kA)-1 = 1/k A-1


![[架构之路-99]:《软件架构设计:程序员向架构师转型必备》-9-确定关键性需求与决定系统架构的因素](https://img-blog.csdnimg.cn/img_convert/6aa84e0496b35cfcf55f48359b3f36ed.png)