统计:多变量时间序列分析 — VMA、VAR、VARMA
一、说明
多变量时间序列是一个在大学课堂上经常被忽视的话题。然而,真实世界的数据通常具有多个维度,我们需要多变量时间序列分析技术。在这篇博客中,我们将通过可视化和 Python 实现 [1] 了解多变量时间序列概念。我假设读者已经知道单变量时间序列分析。如果没有,你可以参考我之前的博客[2]。
目录
- 什么是多变量时间序列?
- 矢量移动平均过程 (VMA)
- 向量自回归过程 (VAR)
- 向量自回归移动平均过程 (VARMA)
- 应用:美国月度零售销售收入
二. 什么是多元时间序列?
顾名思义,多元时间序列是与时间相关的多维数据。我们可以在数学公式中定义多变量时间序列数据,如下所示:

多变量时间序列表示法
其中 Zi,t 是时间 t 的第 i 个分量变量,请注意它是每个 i 和 t 的随机变量。Zt 具有 (m, t) 维数。当我们分析多变量时间序列时,我们不能应用标准的统计理论。这是什么意思?请记住多元线性回归。
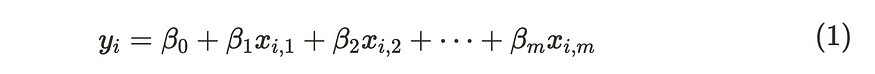
多元线性回归公式
在计算多元线性回归的可能性 (1) 时,我们假设样本的每个观测值 (=习) 都独立于其他观测值。因此,我们可以很容易地通过单个观测值的概率密度的乘积来计算可能性。通常,我们假设观测值遵循正态分布,参数如下 (2)。

多元线性回归的高斯分布及其最大似然估计
然而,在多变量时间序列中,Zt 依赖于 i 和 t。因此,我们不能将相同的假设应用于多元线性回归。要分析多变量时间序列,我们需要了解一些基本概念。让我们深入了解一下。
平稳性
在单变量时间序列中,当时间序列随时间变化具有相同的均值和方差,并且协方差取决于时间滞后时,它具有较弱的平稳性。同样,如果每个分量序列都是弱平稳的,并且其均值和方差是时间不变的,则 m 维多元时间序列也具有平稳性。下图说明了这种情况,以便直观理解。

多元时间序列的平稳性图示
协方差和相关矩阵
现在,让我们考虑一下关于平稳多元时间序列过程 Zt 的统计量。m 维多元时间序列过程的平均值可以写为:
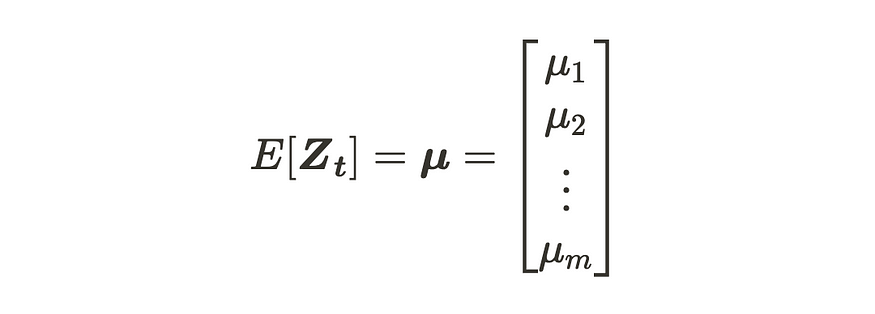
m 维多元时间序列的期望值
平均向量具有 (m, 1) 维。另一方面,滞后 k 协方差矩阵将如下所示:
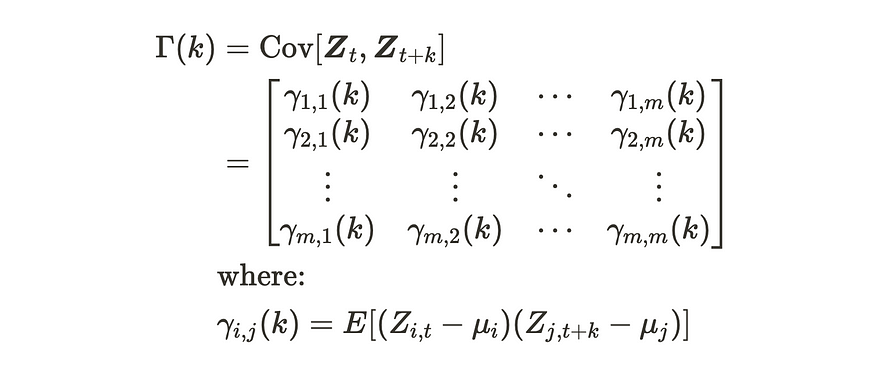
m 维多元时间序列的协方差矩阵
这是证据:

多元时间序列的协方差矩阵的证明
当 k = 0 时,矩阵 Γ(0) 可以很容易地看作是其他变量之间的方差-协方差矩阵。当 k > 0 时,矩阵 Γ(k) 是单变量时间序列的自协方差的展开。我们不仅计算同一变量之间的自协方差,还计算一个变量与其他变量之间的自协方差。
对于相关矩阵,我们只需使用方差矩阵对协方差矩阵进行归一化。

多元时间序列的相关矩阵
其中 D 是对角线矩阵,每个元素是第 i 个分量级数方差。因此,ρ(k) 的第 i 个对角线元素是第 i 个分量序列 Zi,t 的自相关函数,而 ρ(k) 的第 (i, j)个非对角线元素是分量系列 Zi,t 和 Zj,t 之间的互相关函数。
矢量白噪声处理
如果 m 维向量过程 at 具有以下参数,则称为向量白噪声过程。

矢量白噪声处理 (VWN)
其中 Σ 是 (m x m) 对称协方差矩阵。它是白噪声在单变量时间序列中的扩展。白噪声过程的分量在不同时间是不相关的,就像单变量白噪声过程一样。因此,一个向量与其时间滞后向量之间的协方差变为零。请注意,它可能在白噪声过程的各个分量之间同时相关。通常,我们假设高斯白噪声,这意味着 at 遵循多元高斯分布。我们可以将高斯白噪声称为 VWN(0, Σ)。
现在,我们理解了多元时间序列的基本概念。在下一节中,我们将探讨具有代表性的向量时间序列过程,例如 VMA、VAR 和 VARMA。
三、矢量移动平均过程 (VMA)
矢量移动平均 (VMA) 过程是移动平均 (MA) 过程的多维变量版本。让我们快速回顾一下 MA 过程。移动平均线 (MA) 过程由当前冲击和先前冲击的总和 Ut 组成。MA(q)过程可以写在下面的公式中。
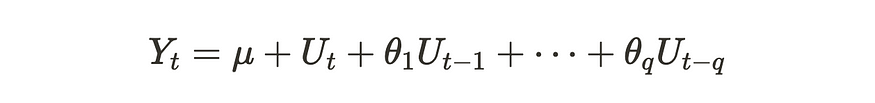
MA(q) 过程
在许多情况下,Ut被认为是白噪声。直观地说,MA(q) 过程具有由前一个 q 步冲击组成的时间序列 {Yt}。请注意,MA(q) 过程是弱平稳的,这意味着均值和方差是恒定的,协方差取决于时间滞后。当我们使用后移运算符 B 时,我们可以按如下方式重写公式:
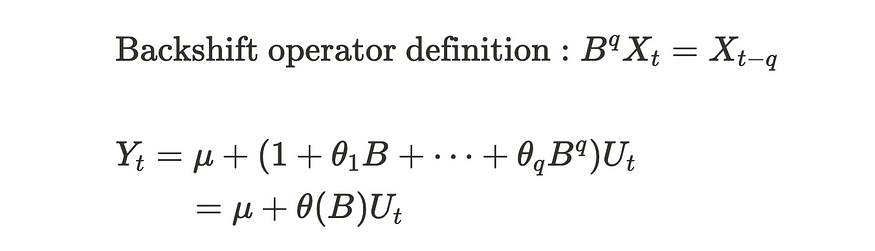
MA(q) 进程由后移算子编写
如您所见,我们可以以有组织的方式重写它。许多教科书都使用这种表达方式。MA(q) 进程具有以下属性。
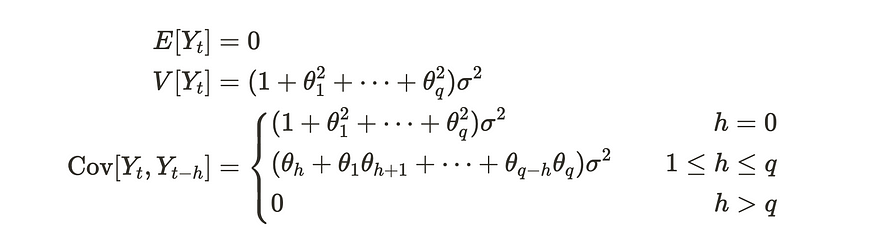
MA(q) 工艺特性
回到 VMA 的话题,它只是 MA 过程的向量形式(=多变量)版本!为了直观地理解 VMA 过程,我们来看一下 m 维 VMA(1) 示例。
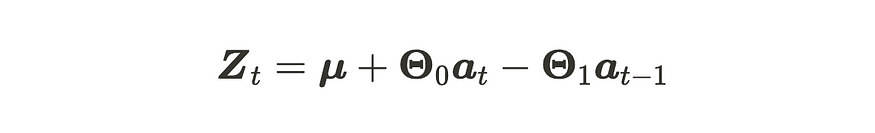
VMA(1) 流程
其中 Zt、μ 和 at 具有 (m, 1) 维,Θ 具有 (m, m) 维。请注意,Θ₀ 是一个单位矩阵。at 是 m 维高斯白噪声过程 VWN(0, Σ) 的序列。VMA(1) 进程具有以下属性。
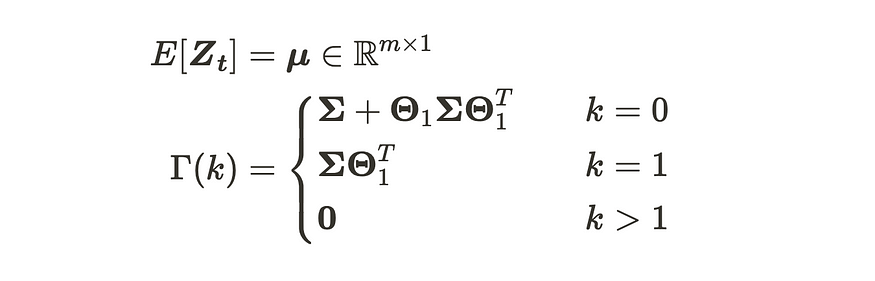
VMA(1) 进程
VMA(1) 过程的均值始终为 μ,因为它由高斯白噪声的和组成,其平均值为 0。另一方面,协方差矩阵似乎有点棘手。让我们通过详细的推导来弄清楚。首先,Γ(0)等价于方差,可以推导如下:
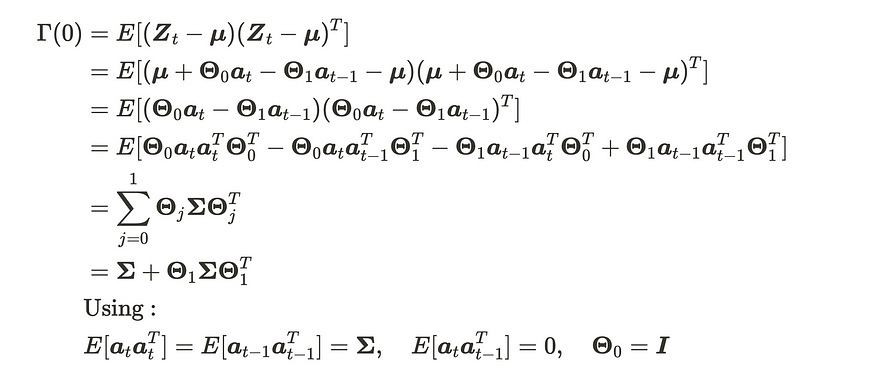
VMA(1) 过程的方差矩阵
可以使用相同的过程来计算以下内容。
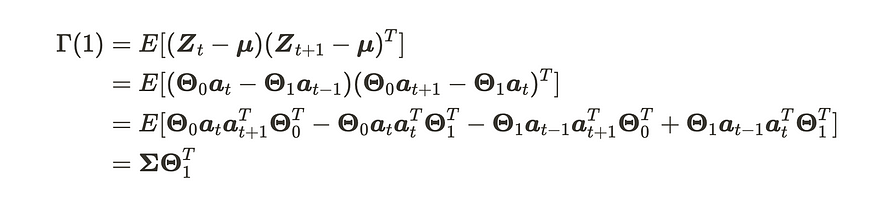
VMA(1) 过程的滞后 1 协方差矩阵
为方便起见,我们在Γ(1)中将负号添加到Θ中。
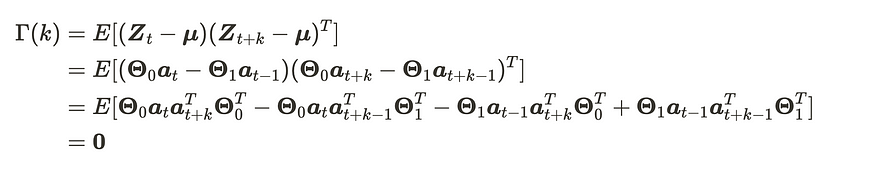
VMA(1) 过程的滞后 k 协方差矩阵
如您所见,均值和自协方差几乎是相似的,但区别在于 VMA 具有 MA 过程参数的矩阵形式。到目前为止,如此模棱两可。让我们用可视化来检查一下具体的例子。我们假设我们满足以下条件。

VMA(1) 进程示例
为简单起见,我们将均值向量设置为零。我们尝试了四个示例系数情况(B1 ~ B4)。下图显示了每个系数情况下 100 个样本的结果。
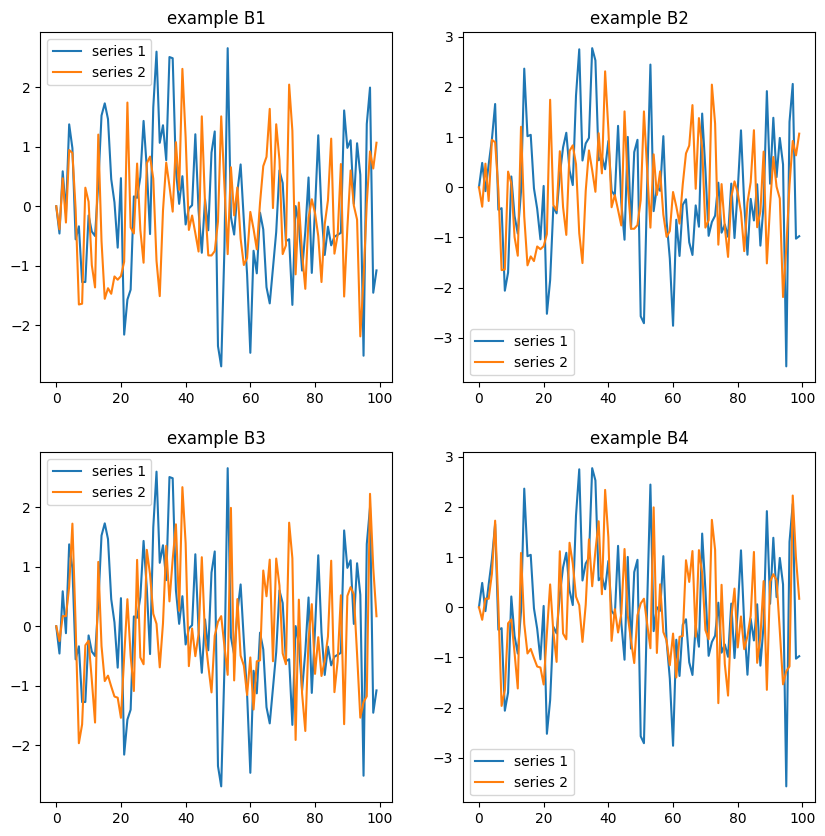
每个系数矩阵的 VMA(1) 过程
在 B1 系数情况下,它们是独立的 MA(1) 过程。在 B2 和 B3 系数情况下,一个序列是独立的 MA(1) 过程,但另一个序列与独立的 MA(1) 过程之一相关。在 B4 系数情况下,这两个序列彼此相关。同样,VMA 过程只是 MA 过程的多变量版本,但由于变量更多,我们必须考虑组件之间的相关性。
现在,让我们将主题扩展到 VMA(q) 过程。m 维 VMA(q) 过程由下式给出:
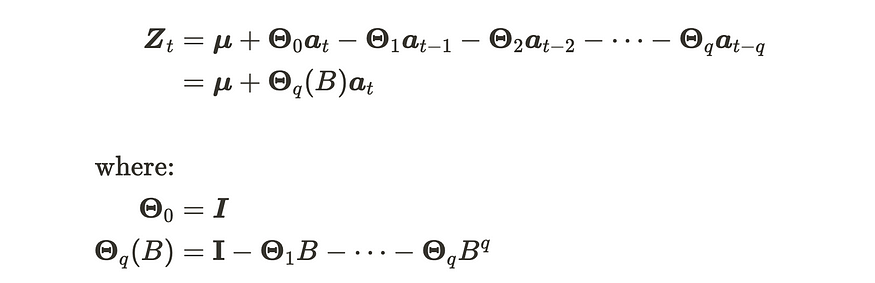
VMA(q)流程的制定
at 是 m 维高斯白噪声过程 VWN(0, Σ) 的序列。VMA(q) 进程具有以下属性。
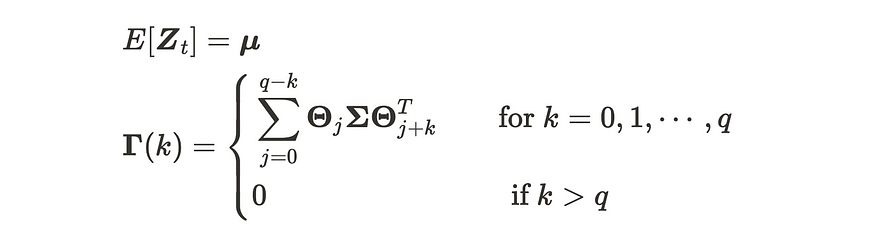
VMA(q) 进程的属性
VMA(q) 过程均值始终为 μ,因为 VMA(q) 由均值为 0 的 VWN 过程组成。另一方面,我们可以按如下方式计算 VMA(q) 过程的协方差矩阵函数。
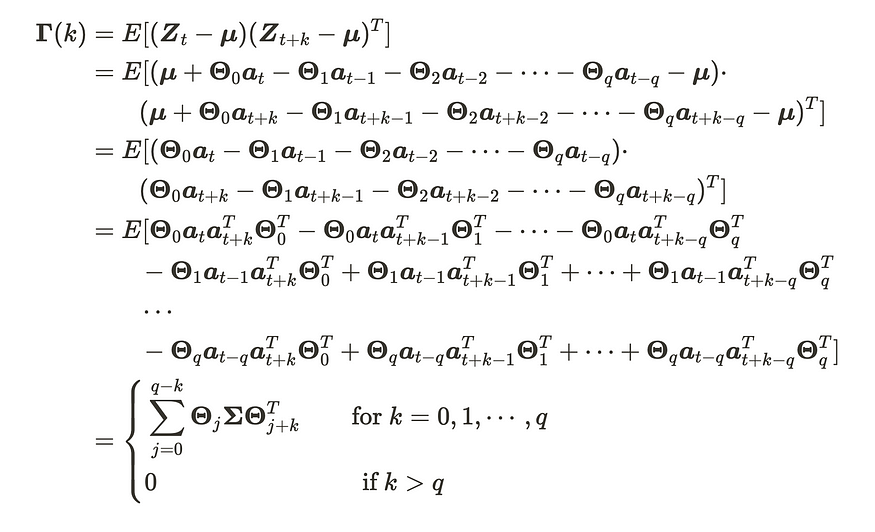
VMA(q) 过程的协方差矩阵
因此,VMA(q) 过程在任何时候都具有平稳性,并且协方差矩阵将在滞后 q 之后被切断。与 MA 过程类似,我们可以利用相关矩阵或 AIC 来确定 q 的顺序。AIC 在定义订单方面更方便,但请注意,AIC 需要计算订单的所有模式,因此需要大量的计算。
在 VMA 部分的最后一部分,有一个重要的概念称为可逆性。如果我们可以将 VMA(q) 过程编写为自回归表示,则它是可逆的,如下所示:
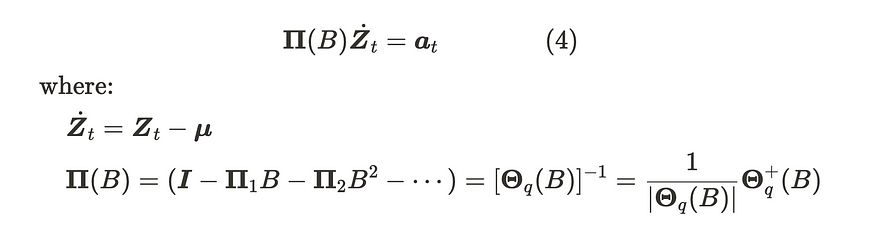
VMA(q) 过程的可逆性
请注意,Θ+(B) 是一个伴随矩阵。我们可以推导出等式(4)如下:
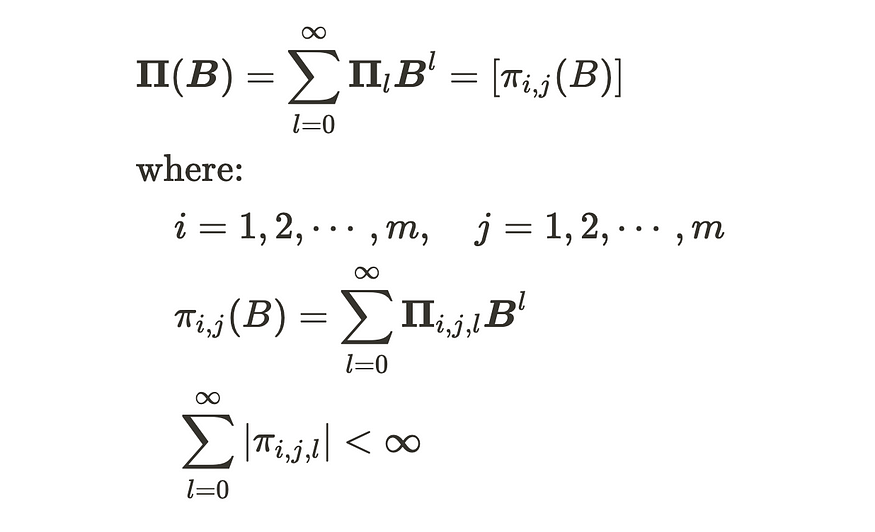
MA 过程的 AR 表示
因此,如果随机过程 (Zt) 是可逆的,则它具有无限自回归表示 (AR(∞))。如果行列式方程的所有根 |Θq(B)|= 0 对单位圆的外侧感到满意,则级数是可逆的。
四、向量自回归过程(VAR)
向量自回归 (VAR) 过程是自回归 (AR) 过程的多维变量版本,类似于 VMA 过程。让我们快速回顾一下 AR 过程。自回归 (AR) 过程使用前一步的值来预测未来值。AR(p)过程可以写在下面的公式中。
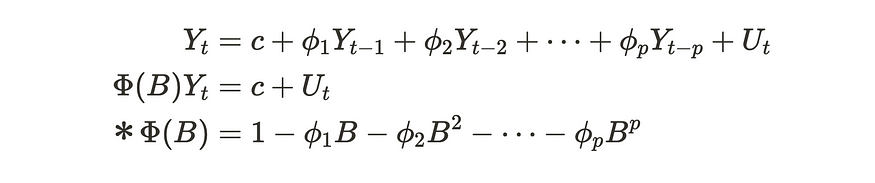
AR(p)过程
假设Ut是白噪声。第二个方程使用后移算子来表示 AR(p) 过程。如果行列式方程的所有根的模量为 |Φ(B)|= 0 表示对单位圆的外侧感到满意。
回到VAR的话题,它又只是AR过程的向量形式(=多变量)版本!为了直观地理解 VAR 过程,让我们考虑 m 维 VAR(1) 示例。
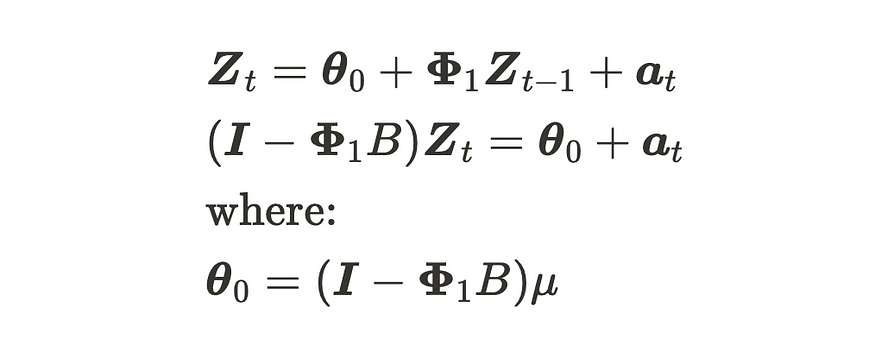
VAR(1)工艺制定
其中 Zt 和 at 具有 (m, 1) 维数,Φ 具有 (m, m) 维数。at 是 m 维高斯白噪声过程 VWN(0, Σ) 的序列。第二个方程使用后移运算符来引用 VAR(1) 方程。显然,该模型是可逆的,因为它是 VAR 模型。如果行列式方程的所有根 |I — 𝚽₁B|= 0 位于单位圆外,VAR(1) 过程是静止的。此外,我们还可以按如下方式转换方程式:
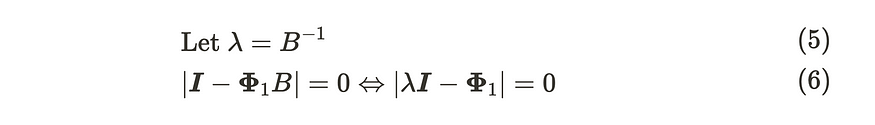
VAR(1) 过程的稳态公式
现在,让我们用可视化来检查具体的例子。我们假设我们满足以下条件。

每个系数矩阵的 VAR(1) 过程
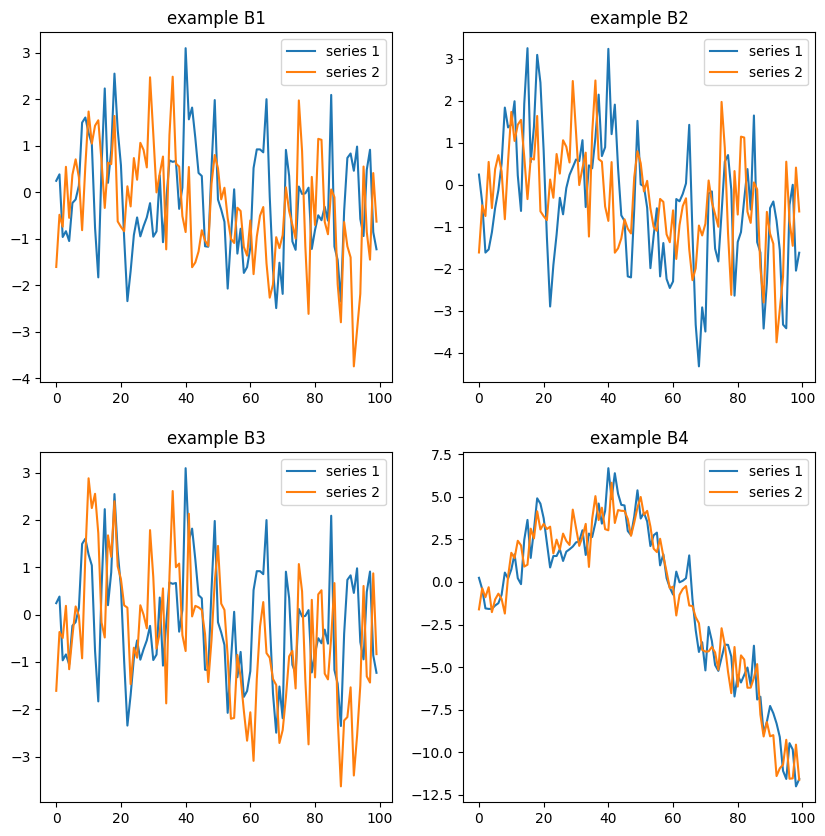
每个系数矩阵的 VAR(1) 过程
在 B1 系数情况下,它们是独立的 AR(1) 过程。同时,在其他系数情况下,一个序列跟随另一个序列。显然,最后一种情况不是静止的。为确保时间序列正确平稳,您需要计算公式 (6) 的特征值。结果如下所示。
<span style="color:rgba(0, 0, 0, 0.8)"><span style="background-color:#ffffff"><span style="background-color:#f9f9f9"><span style="color:#242424"><span style="color:#007400"># sample coefficients of VAR(1) process</span>
B1 = np.array([[<span style="color:#1c00cf">0.5</span>, <span style="color:#1c00cf">0.0</span>], [<span style="color:#1c00cf">0.0</span>, <span style="color:#1c00cf">0.5</span>]])
B2 = np.array([[<span style="color:#1c00cf">0.5</span>, <span style="color:#1c00cf">0.5</span>], [<span style="color:#1c00cf">0.0</span>, <span style="color:#1c00cf">0.5</span>]])
B3 = np.array([[<span style="color:#1c00cf">0.5</span>, <span style="color:#1c00cf">0.0</span>], [<span style="color:#1c00cf">0.5</span>, <span style="color:#1c00cf">0.5</span>]])
B4 = np.array([[<span style="color:#1c00cf">0.5</span>, <span style="color:#1c00cf">0.5</span>], [<span style="color:#1c00cf">0.5</span>, <span style="color:#1c00cf">0.5</span>]])
<span style="color:#007400"># calculate the eigenvalue</span>
<span style="color:#aa0d91">for</span> i, B <span style="color:#aa0d91">in</span> <span style="color:#5c2699">enumerate</span>([B1, B2, B3, B4]):
X = np.eye(<span style="color:#1c00cf">2</span>) - B
w, v = np.linalg.eig(X)
<span style="color:#5c2699">print</span>(w)</span></span></span></span>
每个系数矩阵的特征值
现在,我们可以验证 B1、B2 和 B3 是静止的,但 B4 是非静止的。您还可以使用增强的 Dicky Fuller 检验(如单变量时间序列)检查每个时间序列是否是平稳的。但是,请注意,仅仅检查 VAR 过程的平稳性是不够的。
同样,VAR 过程只是 AR 过程(同样是 VMA 过程)的多变量版本,但由于变量更多,我们必须考虑组件之间的相关性。
现在,让我们将话题扩展到 VAR(p) 过程。m 维 VAR(p) 过程由下式给出:
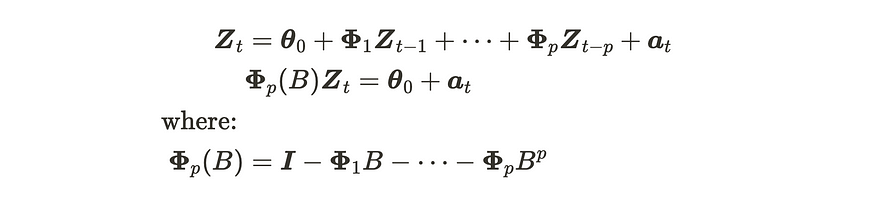
VAR(p)工艺制定
其中 Zt 和 at 具有 (m, 1) 维度,Φ 具有 (m, m) 维度。at 是 m 维高斯白噪声过程 VWN(0, Σ) 的序列。由于AR(p)过程是可逆的,并且如果|Φp(B)|= 0 位于单位圆外,过程是静止的。它与 AR(p) 过程相同,但 VAR(p) 是矢量化版本。
当 AR(p) 过程是平稳的时,它具有以下均值和协方差。
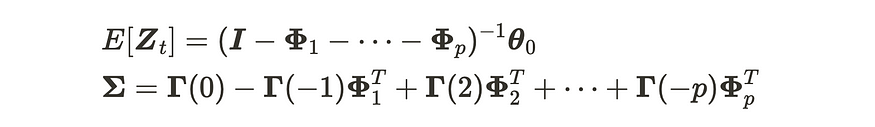
AR(p)过程的特性
首先,我们可以按如下方式推导出平均值:
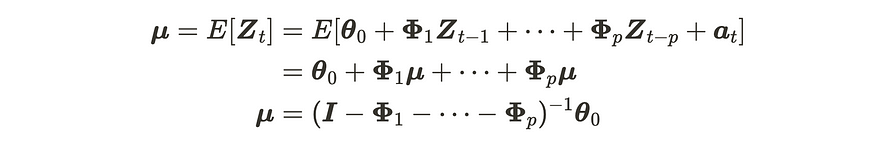
AR(p) 过程均值的推导
推导协方差很棘手。第一步,我们需要推导出 θ 值。
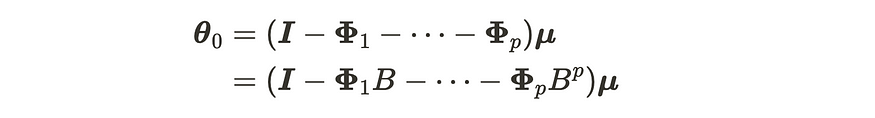
偏倚项的推导
我们可以推导出第二个方程,因为μ总是恒定的。接下来,我们需要转换 VAR(p) 方程。
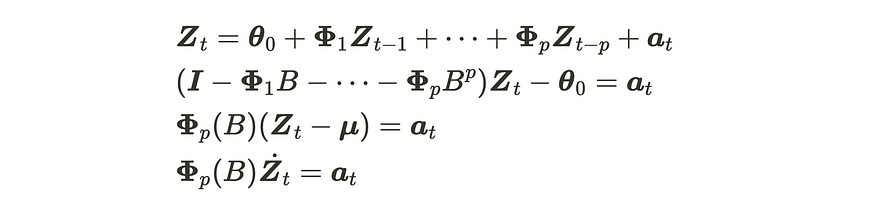
你不是已经看过类似于最后一个方程式的公式了吗?我们已经在 VMA 部分看到了这一点。如果 VAR(p) 过程是静止的,则可以将其编写为 VMA 表示。
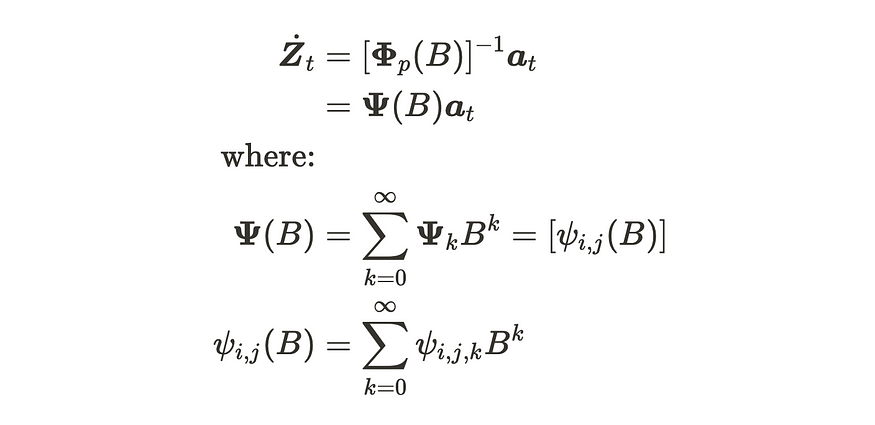
VAR 过程的 VMA 表示
然后,协方差矩阵的计算公式为:
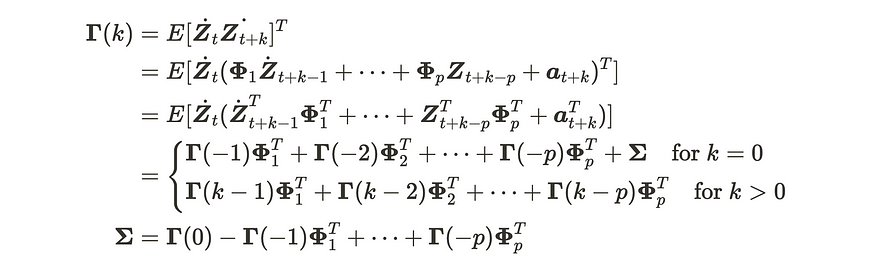
VAR(p) 过程的协方差矩阵
在公式中,它由广义 Yule-Walker 矩阵方程推导而来。虽然我跳过了这篇博客中的解释,但你可以参考这个讲座pdf [3]。综上所述,如果VAR或VMA满足特定条件,它们可以相互转换。
与 AR 过程类似,我们可以利用偏相关矩阵来找到顺序。同样,AIC也可以使用,并且更方便。请注意,AIC需要计算订单的所有模式,因此需要大量的计算。因此,如果有很多变量并且似乎有很多滞后,那么使用相关矩阵仍然是一个很好的方法。
到目前为止,我们已经了解了 VMA 和 VAR 流程。在单变量时间序列中,有 ARMA 过程,它与 AR 和 MA 过程相结合。是的,我们也有用于多变量时间序列的 VARMA。在最后的理论部分,我们将学习 VARMA 过程。
五、向量自回归移动平均过程 (VARMA)
VARMA 过程是 VAR 和 VMA 过程的组合。m 维向量自回归移动平均 (VARMA) 过程有阶数 p 和 q,分别对应 VAR 和 VMA 过程,可以描述为:
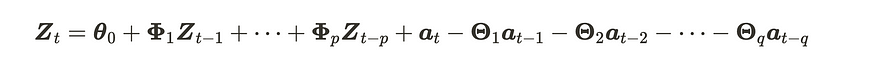
VARMA(p,q)工艺配方
我们称之为 VARMA(p, q)。我们可以将这个方程式重新表述为:
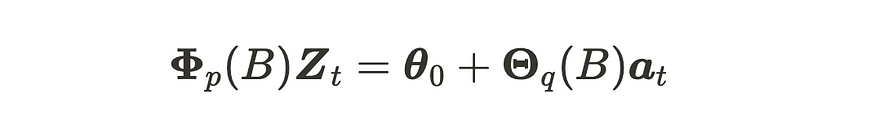
同样,其中 Zt 和 at 具有 (m, 1) 维,Φ 和 Θ 具有 (m, m) 维。at 是 m 维高斯白噪声过程 VWN(0, Σ) 的序列。
由于 VMA 过程是平稳的,因此平稳性取决于 VAR 项。因此,当 |Φp(B)|= 0 位于单位圆外,VARMA 过程是静止的。同时,可逆性取决于 VMA 项。如果行列式多项式的所有根 |Θq(B)|= 0 位于单位圆外,VARMA 过程是可逆的。
让我们回顾一下 VMA、VAR 和 VARMA 过程。它们具有类似于单变量时间序列的想法,但它们在多变量时间序列中具有多维数据。因此,我们不仅需要考虑当前时间步长与上一个时间步长之间的相关性,还需要考虑变量之间的相关性。多变量时间序列的理论部分到此结束。现在,让我们使用具体的例子来实现它们!
六、应用:美国月度零售销售收入
在最后一节中,我们将在 Python 中实现多变量时间序列。对于第一个示例,我们将使用 [1] 中引用的美国月度零售销售收入。它包含2009年6月至2016年11月的AUT(汽车)、BUM(建材)、GEM(日用百货)、COM(消费品)和HOA(家用电器)五个行业,其中n=90。每个时间序列数据如下所示:
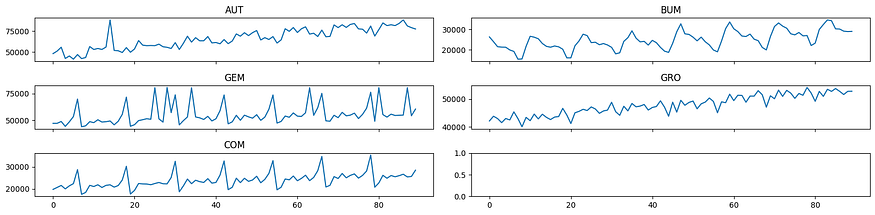
每个时间序列的图形
显然,它们是非静止的。因此,让我们试着对它们进行差分。
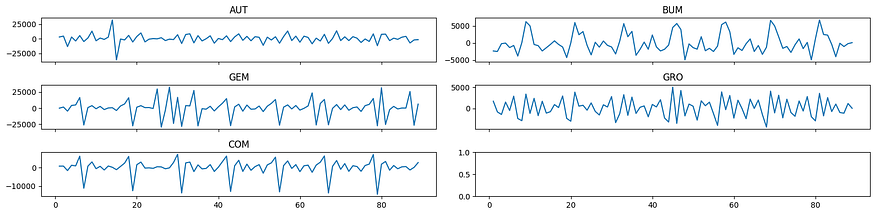
每个时间序列的图表取差异
现在,情况好多了。似乎存在季节性,这是一种定期的数据集变化,但为了简单起见,我将在此博客中忽略它。此外,该系列不是完全静止的,因此我将使用 VAR 和 VARMA 模型。在 Python 中,你可以使用 statsmodels 轻松实现 VAR 和 VARMA 建模(如果你想构建 VMA,也可以使用 statsmodels)。
VAR建模
对于 VAR 建模,我们可以选择要计算的最大阶数,模型会根据给定的标准(例如 AIC)自动选择最佳模型。在以下示例中,我选择 5 作为最大延迟。
var = sm.tsa.VAR(diff_df)
result = var.fit(maxlags=5, ic='aic')
result.summary()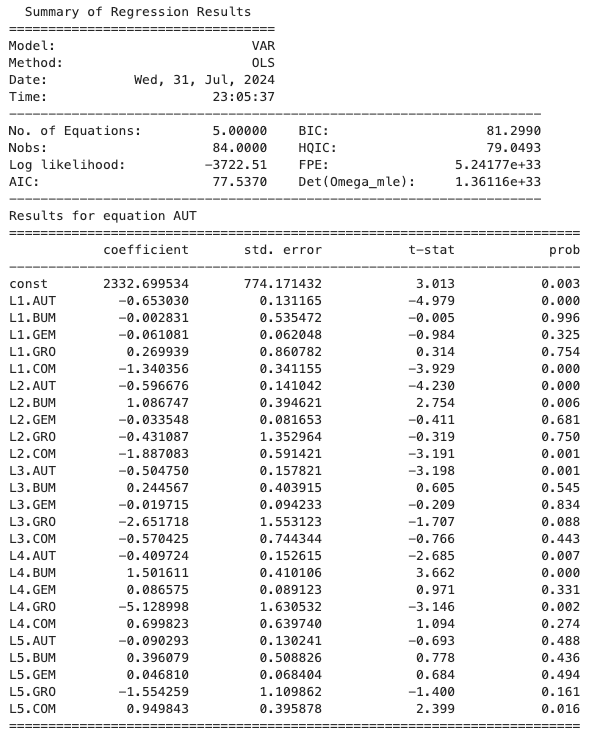
VAR 估计结果的一部分
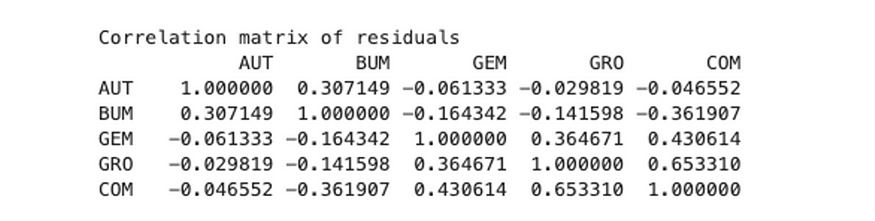
残差的相关矩阵
在这种情况下,最好的模型是五滞后的模型。结果图如下图。相关矩阵显示变量(如 COM 和 GRO)之间的相关性。因此,它仍然不是静止的。残差自相关函数的结果图如下图。
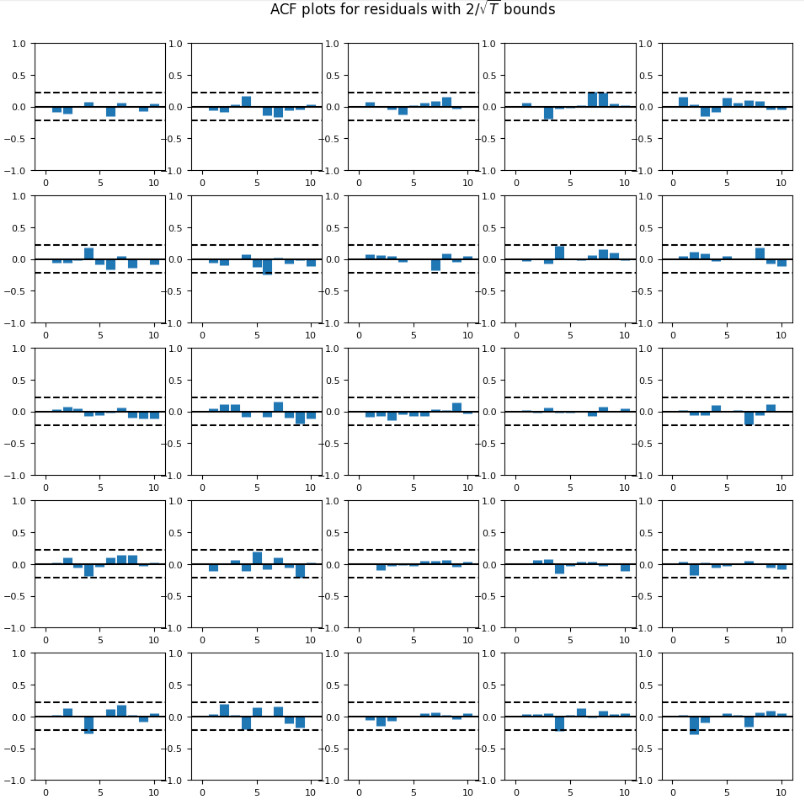
残差的自相关图
正如你所看到的,存在一些相关性。因此,通过调整参数来改进模型是有改进空间的。
VARMA 建模
对于 VARMA 建模,没有内置函数来为我们选择最佳顺序。因此,我们需要迭代订单的组合。
# modeling
results = pd.DataFrame(columns=['p', 'q', 'AIC'])
for p in range(1, 5):
for q in range(1, 5):
model = sm.tsa.VARMAX(diff_df, order=(p, q))
result = model.fit(maxiter=1000, disp=False)
results = results.append({'p': p, 'q': q, 'AIC': result.aic})
res_df = pd.DataFrame(results, columns=['p', 'q', 'AIC'])
res_df.sort_values(by=['AIC']).head()这需要几分钟才能完成。请注意,VARMA 计算通常不稳定,因此 VAR 模型在实践中更好。这是结果。

VARMA 模型的结果
如您所见,VARMA(4, 1) 是本例中的最佳模型,它与 VAR 模型的顺序相同。根据 VAR 和 VARMA 结果,阶数 q 越小越好。如果我们想创建一个更拟合的模型,我们需要考虑季节性分量。Meta 的 Prophet 库似乎可以方便地构建模型,也是一个不错的选择。让我们试一次。
我使用的代码在这里:
from copy import deepcopy
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima_process import ArmaProcess
from statsmodels.tsa.stattools import acovf, acf
import statsmodels.api as smVMA(1) process
# VMA(1) process simulated data
sample_num = 100
mean = np.array([0, 0])
cov = np.array([[1, 0], [0, 1]])
error_vec = np.random.multivariate_normal(mean, cov, sample_num).T
print(error_vec.shape)
# sample coefficients of VMA(1) process
B1 = np.array([[0.5, 0.0], [0.0, 0.5]])
B2 = np.array([[0.5, 0.5], [0.0, 0.5]])
B3 = np.array([[0.5, 0.0], [0.5, 0.5]])
B4 = np.array([[0.5, 0.5], [0.5, 0.5]])def generate_VMA(error_vec: np.array, B: np.array) -> np.array:
"""
Generate the VMA process
"""
res = np.zeros((sample_num, 2))
for j in range(1, sample_num):
e_current = error_vec[:, j].reshape(2, 1)
e_previous = error_vec[:, j-1].reshape(2, 1)
res[j] = calculate_VMA(e_current, e_previous, B).T
return res
def calculate_VMA(e_current: np.array, e_previous: np.array, B: np.array) -> np.array:
"""
Calculate VMA(1) process value
args:
e_current [np.array] : the error term at the current step
e_previous [np.array] : the error term at the previous step
B [np.array] : the coefficient matrix of the VMA(1) process
return:
y_current [np.array] : the calculation result of the VMA(1) process
"""
y_current = e_current + np.dot(B, e_previous).reshape(2, 1)
return y_current
fig, ax = plt.subplots(2, 2, figsize=(10, 10))
for i, B in enumerate([B1, B2, B3, B4]):
x = i // 2
y = i % 2
res = generate_VMA(error_vec, B)
ax[x, y].plot(res, label=['series 1', 'series 2'])
ax[x, y].set_title(f'example B{str(i+1)}')
ax[x, y].legend()
plt.legend()
plt.show()
VAR(1)
# VAR(1) process simulated data
sample_num = 100
mean = np.array([0, 0])
cov = np.array([[1, 0], [0, 1]])
error_vec = np.random.multivariate_normal(mean, cov, sample_num).T
print(error_vec.shape)
# sample coefficients of VAR(1) process
B1 = np.array([[0.5, 0.0], [0.0, 0.5]])
B2 = np.array([[0.5, 0.5], [0.0, 0.5]])
B3 = np.array([[0.5, 0.0], [0.5, 0.5]])
B4 = np.array([[0.5, 0.5], [0.5, 0.5]])fig, ax = plt.subplots(2, 2, figsize=(10, 10))
for i, B in enumerate([B1, B2, B3, B4]):
x = i // 2
y = i % 2
res = np.zeros((sample_num, 2))
previous_z = np.array([0, 0]).reshape(2, 1)
for j in range(sample_num):
a_t = error_vec[:, j].reshape(2, 1)
res[j] = (np.dot(B, previous_z) + a_t).T
previous_z = res[j].reshape(2, 1)
ax[x, y].plot(res, label=['series 1', 'series 2'])
ax[x, y].set_title(f'example B{str(i+1)}')
ax[x, y].legend()
plt.legend()
plt.show()
# sample coefficients of VAR(1) process
B1 = np.array([[0.5, 0.0], [0.0, 0.5]])
B2 = np.array([[0.5, 0.5], [0.0, 0.5]])
B3 = np.array([[0.5, 0.0], [0.5, 0.5]])
B4 = np.array([[0.5, 0.5], [0.5, 0.5]])
B_names = ["B1", "B2", "B3", "B4"]
# calculate the eigenvalue
for i, B in enumerate([B1, B2, B3, B4]):
X = np.eye(2) - B
w, v = np.linalg.eig(X)
print(B_names[i], w)B1 [0.5 0.5]
B2 [0.5 0.5]
B3 [0.5 0.5]
B4 [1.00000000e+00 1.11022302e-16]
# sample coefficients of VAR(1) process
B1 = np.array([[1.9, 1.3], [0.1, 0.8]])
B2 = np.array([[0.1, 0.0], [0.0, 0.1]])
# calculate the eigenvalue
for i, B in enumerate([B1, B2]):
X = np.eye(2) - B
w, v = np.linalg.eig(X)
print(w)[-1.00764732 0.30764732] [0.9 0.9]
Application
In [94]:
df = pd.read_csv('US_monthly_retail_dataset.csv')
df.head()PeriodAUTBUMGEMGROCOM0June 0948078263504708942146198221July 0951093240034709743838207042August 0955677215224882642994216093September 0942299213044420241537200504October 094526821263485094302021425
| Period | AUT | BUM | GEM | GRO | COM | |
|---|---|---|---|---|---|---|
| June 09 | 48078 | 26350 | 47089 | 42146 | 19822 | |
| July 09 | 51093 | 24003 | 47097 | 43838 | 20704 | |
| August 09 | 55677 | 21522 | 48826 | 42994 | 21609 | |
| September 09 | 42299 | 21304 | 44202 | 41537 | 20050 | |
| October 09 | 45268 | 21263 | 48509 | 43020 | 21425 | |
| November 09 | 41448 | 19915 | 53489 | 42508 | 22439 | |
| December 09 | 46936 | 19182 | 69970 | 45395 | 28782 | |
| January 10 | 42143 | 15349 | 43854 | 42986 | 17570 | |
| February 10 | 43434 | 15468 | 44756 | 40061 | 18443 | |
| March 10 | 56482 | 21692 | 48643 | 43433 | 21649 | |
| April 10 | 52987 | 26682 | 47751 | 42236 | 21126 | |
| May 10 | 54178 | 26231 | 50476 | 44604 | 21913 | |
| June 10 | 53049 | 25446 | 48290 | 42877 | 20688 | |
| July 10 | 55854 | 23100 | 48620 | 44558 | 21650 | |
| August 10 | 88120 | 21698 | 49314 | 43431 | 21904 | |
| September 10 | 51886 | 21261 | 45678 | 42642 | 20841 | |
| October 10 | 51463 | 21882 | 49037 | 43535 | 21568 | |
| November 10 | 49393 | 21458 | 55587 | 43723 | 24094 | |
| December 10 | 55231 | 20277 | 71770 | 46656 | 30297 | |
| January 11 | 49692 | 16006 | 44323 | 44280 | 17698 | |
| February 11 | 53590 | 16003 | 45808 | 41229 | 19364 | |
| March 11 | 63583 | 21964 | 49677 | 45069 | 22481 | |
| April 11 | 58199 | 24377 | 50482 | 45586 | 22302 | |
| May 11 | 57518 | 27709 | 51437 | 46319 | 22251 | |
| June 11 | 57722 | 27009 | 50907 | 45883 | 21925 | |
| July 11 | 57538 | 23530 | 80661 | 47170 | 22490 | |
| August 11 | 59341 | 23733 | 51267 | 46449 | 22951 | |
| September 11 | 56231 | 22501 | 48238 | 44876 | 22379 | |
| October 11 | 55574 | 23077 | 80877 | 45725 | 22324 | |
| November 11 | 54186 | 22371 | 57198 | 46045 | 25196 | |
| December 11 | 61128 | 21201 | 73907 | 48840 | 32555 | |
| January 12 | 52989 | 17981 | 45642 | 45460 | 18740 | |
| Febuary 12 | 60345 | 18502 | 49635 | 44172 | 21403 | |
| March 12 | 68799 | 24156 | 53114 | 47406 | 24511 | |
| April 12 | 61761 | 25987 | 80601 | 45753 | 22406 | |
| May 12 | 67063 | 29374 | 53091 | 48418 | 23965 | |
| June 12 | 63336 | 25772 | 52279 | 47215 | 23332 | |
| July 12 | 63364 | 23921 | 50733 | 47472 | 22968 | |
| August 12 | 68423 | 24170 | 53679 | 48046 | 24691 | |
| September 12 | 60831 | 22327 | 49326 | 46048 | 22654 | |
| October 12 | 61295 | 24659 | 51398 | 46978 | 22970 | |
| November 12 | 59772 | 23512 | 59013 | 47314 | 26318 | |
| December 12 | 64800 | 21172 | 73802 | 49363 | 32705 | |
| January 13 | 59912 | 19323 | 46616 | 47082 | 19688 | |
| February 13 | 63076 | 18702 | 48503 | 43837 | 20780 | |
| March 13 | 71529 | 23216 | 54650 | 48869 | 24887 | |
| April 13 | 68820 | 28906 | 49955 | 45316 | 22885 | |
| May 13 | 72952 | 32849 | 54774 | 49549 | 24860 | |
| June 13 | 69509 | 27891 | 53179 | 47765 | 23471 | |
| Ju1y 13 | 73058 | 27611 | 51958 | 48783 | 24090 | |
| August 13 | 75544 | 26242 | 55227 | 49288 | 25797 | |
| September 13 | 64308 | 24424 | 49910 | 46499 | 22819 | |
| October 13 | 67070 | 26255 | 52923 | 48283 | 24366 | |
| November 13 | 64894 | 23974 | 60375 | 48904 | 27057 | |
| December 13 | 68348 | 22399 | 73798 | 50374 | 32857 | |
| January 14 | 60664 | 19900 | 47319 | 49142 | 19624 | |
| February 14 | 64398 | 18989 | 48886 | 45091 | 20796 | |
| March 14 | 77683 | 24343 | 53967 | 48997 | 24533 | |
| April 14 | 74600 | 30447 | 52789 | 48690 | 24153 | |
| May 14 | 79113 | 33758 | 56900 | 51742 | 25878 | |
| June 14 | 73221 | 30409 | 53872 | 49434 | 23740 | |
| Ju1y 14 | 77685 | 29003 | 53646 | 51362 | 24818 | |
| August 14 | 79966 | 26798 | 57050 | 51309 | 26257 | |
| September 14 | 71294 | 26574 | 80663 | 48861 | 23771 | |
| October 14 | 72328 | 27748 | 54625 | 51057 | 25243 | |
| November 14 | 68450 | 25248 | 61843 | 51042 | 28293 | |
| December 14 | 76041 | 24498 | 75313 | 53011 | 34750 | |
| January 15 | 68158 | 21161 | 49436 | 51536 | 20906 | |
| February 15 | 68559 | 19923 | 49100 | 47088 | 21655 | |
| March 15 | 82234 | 26526 | 54686 | 51167 | 25617 | |
| April 15 | 79070 | 31512 | 52424 | 50091 | 24765 | |
| May 15 | 82410 | 33282 | 57441 | 53201 | 27034 | |
| June 15 | 79265 | 31709 | 54135 | 50950 | 25077 | |
| July 15 | 82841 | 30676 | 54829 | 53116 | 26170 | |
| August 15 | 83872 | 27916 | 56674 | 52120 | 26847 | |
| September 15 | 77506 | 27377 | 51588 | 50244 | 24919 | |
| October 15 | 77134 | 28546 | 55544 | 51987 | 26163 | |
| November 15 | 72505 | 26889 | 61397 | 51355 | 28156 | |
| December 15 | 80868 | 27044 | 76391 | 54146 | 35386 | |
| January 16 | 68984 | 22100 | 49050 | 52167 | 20809 | |
| February 16 | 76652 | 23290 | 80661 | 49193 | 22750 | |
| March 16 | 84611 | 30027 | 55303 | 52741 | 26205 | |
| April 16 | 81446 | 32496 | 52960 | 50958 | 24867 | |
| May 16 | 82428 | 34787 | 55722 | 53502 | 26097 | |
| June 16 | 81439 | 34371 | 54481 | 52745 | 25549 | |
| July 16 | 84085 | 30347 | 54710 | 53756 | 26045 | |
| August 16 | 88224 | 30257 | 54859 | 52769 | 26693 | |
| September 16 | 81027 | 29210 | 80670 | 51621 | 25469 | |
| October 16 | 78994 | 29010 | 54221 | 52769 | 25686 | |
| November 16 | 77389 | 29095 | 60520 | 52793 | 28524 |
统计:多变量时间序列分析 — VMA、VAR、VARMA |由 Yuki Shizuya |直觉 |2024年8月 |中等 (medium.com)
本博客到此结束。感谢您抽出宝贵时间阅读我的博客!