发表于:CIKM
推荐指数: #paper/⭐
一句话总结:融合了GCN(A,X)和GCN(A,I),创新性不足,因此只能B会
流程:

融合部分:
h
i
f
=
h
i
s
+
λ
i
h
i
c
h_i^f=h_i^s+\lambda_ih_i^c
hif=his+λihic
由于有n个
λ
\lambda
λ.因此作者加了如下优化:
L
ϕ
=
∑
i
=
1
N
λ
i
s
(
h
i
s
,
h
i
c
)
+
α
1
∣
∣
λ
∣
∣
2
+
α
2
∣
1
N
∑
i
=
1
N
λ
i
−
ϵ
∣
\mathcal{L}_\phi=\sum_{i=1}^N\lambda_is\left(h_i^s,h_i^c\right)+\alpha_1||\lambda||_2+\alpha_2\left|\frac1N\sum_{i=1}^N\lambda_i-\epsilon\right|
Lϕ=i=1∑Nλis(his,hic)+α1∣∣λ∣∣2+α2
N1i=1∑Nλi−ϵ
MUSE Multi-View Contrastive Learningfor Heterophilic Graphs
news2026/2/13 21:53:10
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1979369.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
贪心算法之货仓选址问题
#include<stdio.h>
#include<stdlib.h>
#include<math.h>//贪心算法之货仓选址问题/*** void* p是万能指针,可以和其它任意类型的指针进行转换,前提是确保转换是合法的*/
//写好用于qsort的比较函数,这里写的函数一般用于…
【K8S】为什么需要Kubernetes?
文章目录 1 什么是Kubernetes?2 三种常见的应用部署方式2.1 传统部署2.2 虚拟化部署2.3 容器化部署 3 Kubernetes的特点写在最后 1 什么是Kubernetes?
Kubernetes是 一个开源的,用于管理云平台中多个主机上的容器化应用,Kubernet…
分享6款有助于写论文能用到的软件app!
在学术写作中,选择合适的软件和工具可以大大提高效率和质量。以下是六款有助于写论文的软件app推荐,其中特别重点介绍千笔-AIPassPaPer这款AI原创论文写作平台。
1. 千笔-AIPassPaPer
千笔-AIPassPaPer是一款功能全面且高效的AI原创论文写作平台。它能…
RabbitMQ高级特性 - 非持久化 / 持久化(交换机、队列、消息)
文章目录 RabbitMQ 持久化机制概述实现非持久化(交换机、队列、消息)实现持久化(交换机、队列、消息) RabbitMQ 持久化机制 概述
前面讲到了 生产者消息确认机制 和 消费者消息确认机制,保证了消息传输的可靠性&#…
断电引起redo和数据文件不一致故障恢复---惜分飞
有些时候故障总是来的让人非常意外,这个在准备停机迁移数据库之前的几分钟由于某种原因直接导致主机掉电,再次开机数据库无法启动 Sat Aug 03 23:10:37 2024 Successful mount of redo thread 1, with mount id 3696805928 Database mounted in Exclusive Mode Lost write prot…
【考研高数】tan(arcsin x)、tan(arccos x)、sin(arccos x)、cos(arcsin x) 等于多少?
在做题的时候,我们可能会用到下面这几个式子的值,在这里,「荒原之梦考研数学」先给出结论,在这些结论的后面,也给同学们放上了具体的证明过程: tan ( arcsin x ) x 1 − x 2 \tan(\arcsin x) \frac…
深度分析AI大模型赋能后,内容生产行业的发展现状
国内首部由AI全流程参与制作的微短剧《补天》近日正式发布,从剧本构思、角色设定到场景设计以及后期剪辑,各个环节均深度融入了AI技术,展现了人工智能在内容创作方面的全面能力。
AI大模型的兴起正在深刻地改变着内容生产的方式,…
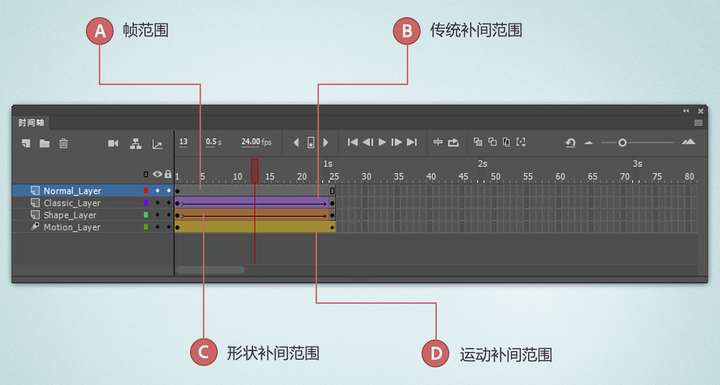
Animate软件基本概念:帧及关键帧
FlashASer:AdobeAnimate2021软件零基础入门教程https://zhuanlan.zhihu.com/p/633230084
FlashASer:实用的各种Adobe Animate软件教程https://zhuanlan.zhihu.com/p/675680471
FlashASer:Animate教程及作品源文件https://zhuanlan.zhihu.co…
VBA读取不带后缀名文本文件的方法(解决Unix文本文件在Windows下变成一行的读取)
VBA在操作Excel等Office软件方面有天然的优势,虽说现在Python的Pandas,openpyxl和Java的poi包都可以处理Excel文件,但有两个问题:首先,目标电脑上必须先按照Java或python环境,如果在一些机构内部处于安全原…
库存超卖问题解决方式
文章目录 超卖问题解决方式什么是库存超卖问题?乐观锁和悲观锁的定义超卖问题解决方式一、悲观锁1.jvm单机锁2.通过使用mysql的行锁,使用一个sql解决并发访问问题3.使用mysql的悲观锁解决4. 使用redis分布式锁来解决 二、乐观锁解决1.版本号2. CAS法&…
Problems with OpenAI Authentification
题意:OpenAI 认证问题 问题背景:
Ive got some problems with the Authentification to OpenAI in my python code. It seems like, OpenAI doesnt accept my key. I did a new on and tried it with other ones before. I always get the same issues.…
机械学习—零基础学习日志(高数21——泰勒展开)
零基础为了学人工智能,真的开始复习高数
求解自然对话e,证明e是如何从极限(11/x)x中得来的,需要了解泰勒展开式。现在终于学习到泰勒展开式。
泰勒公式定义 泰勒公式具体展开 泰勒公式考点常用
这里也可以等价到函数…
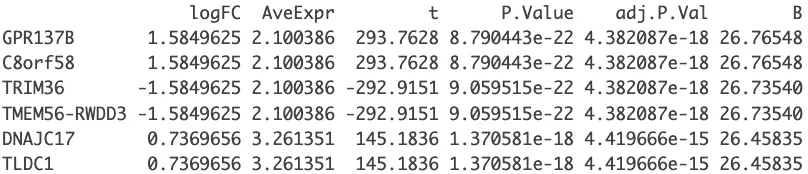
转录组差异分析方法整理(deseq2,edgeR,limma_voom)
三种最常用的差异分析方法(deseq2,edgeR,limma_voom)的整理。
目前在实际应用的过程中一般选择其中一种结果即可,或三种方法分析后结果取交集。 本次演示选择了GSE213615数据集,该数据集采用了两种肝癌细胞系,并使用索…
鸿蒙媒体开发【相机数据采集保存】音频和视频
相机数据采集保存
介绍
本示例主要展示了相机的相关功能,使用libohcamera.so 接口实现相机的预览、拍照、录像、前后置摄像头切换进行拍照、录像,以及对焦、曝光等控制类功能。
效果预览 使用说明
弹出是否允许“CameraSample”使用相机?…
CentOS上面的MySQL安装~~~保姆级教程
目录 0.声明
1.下载官网包包
2.新建文件夹,把rpm拖拽进来
3.安装yum源,查看前后变化
4.安装mysql服务
5.查看是否安装成功
6.出现报错的解决方案
7.启动MySQL
8.查看启动服务
9.配置文件
10.重新运行
11.免密码登录
12.再谈配置文件 0.声明…
【Unity】3D功能开发入门系列(四)
Unity3D功能开发入门系列(四) 一、组件的访问(一)组件的调用(二)组件的参数(三)引用别的组件(四)引用脚本组件(五)消息调用 二、物体的…
A*搜索算法 双向A*搜索算法 Julia实现
算法概述
抽象的在非负有向边权图 G ( V , E , W ) , W : E → R G (V, E, W), W: E \to \mathbb{R} G(V,E,W),W:E→R 上的 BFS 过程可以看作这样: (1) 设 C C C 点集表示已遍历的点, ∀ n ∈ C , d ( n ) \forall n \in C, d(n) ∀n∈C,d(n) 表示…
Leetcode75- 种花问题
间隔种花 也就是 0 0 0 或者开头 0 0 结尾 0 0
也就是这三个地方可以种花 然后分别判断 最后根据提交结果分析漏掉的情况
比如 n为0 和 数组长度只有一个的情况
使用枚举可以很快解题
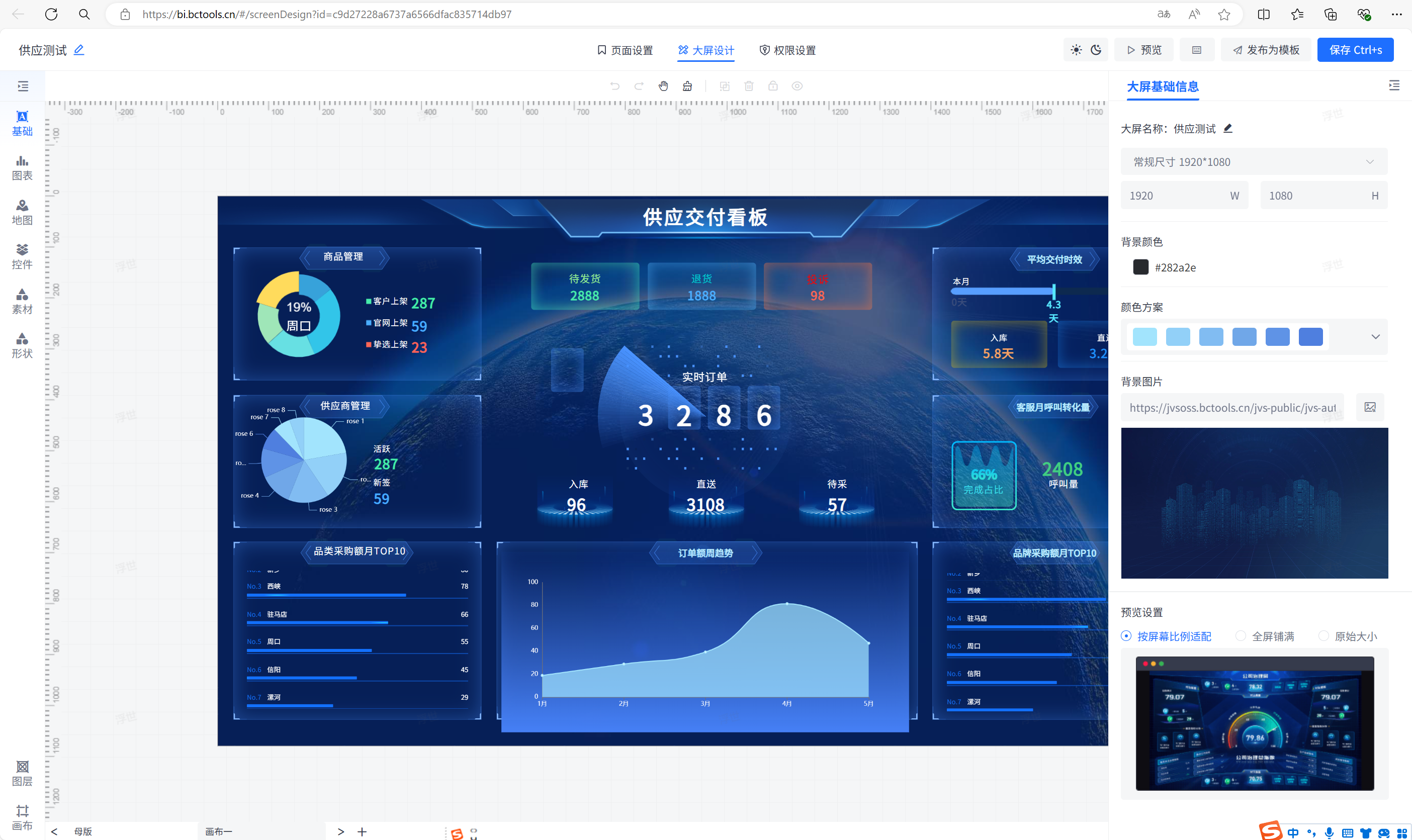
技术男的审美反击:UI配置化新纪元
之前常常被甲方的领导说,我们全是一群钢铁直男,一点不懂审美,其实我们心里边想的 “您说得对啊!!!!” 这个可能和理工科有关系吧,理工男好像都差不多,所以这次我们就把很…