Face2V SDK适用于需要人脸检测、人脸特征点和特征向量提取的应用,提供Web API和原生API。官方下载地址:Face2V SDK 。
1、目录组织
Face2V SDK开发包的目录组织说明如下:
face2v_sdk
| - core # 核心代码目录
| - face_detector.py # 人脸检测器实现类
| - landmark_regressor.py # 人脸特征点回归器实现类
| - embedding_extractor.py # 人脸特征向量提取器实现类
| - models # 预训练模型目录
| - samples # 测试图片目录
| - serve.py # Web UI/API 启动代码
| - web_api_test.py # Web API测试代码
| - native_api_test.py # Native API测试代码
| - requirements.txt # 依赖包描述文件
在第一次使用之前,首先安装依赖文件:
pip install -r requirements.txt
2、使用Web UI
执行如下命令启动Web UI:
python serve.py
然后使用浏览器访问 http://127.0.0.1:7860,即可打开Web UI。
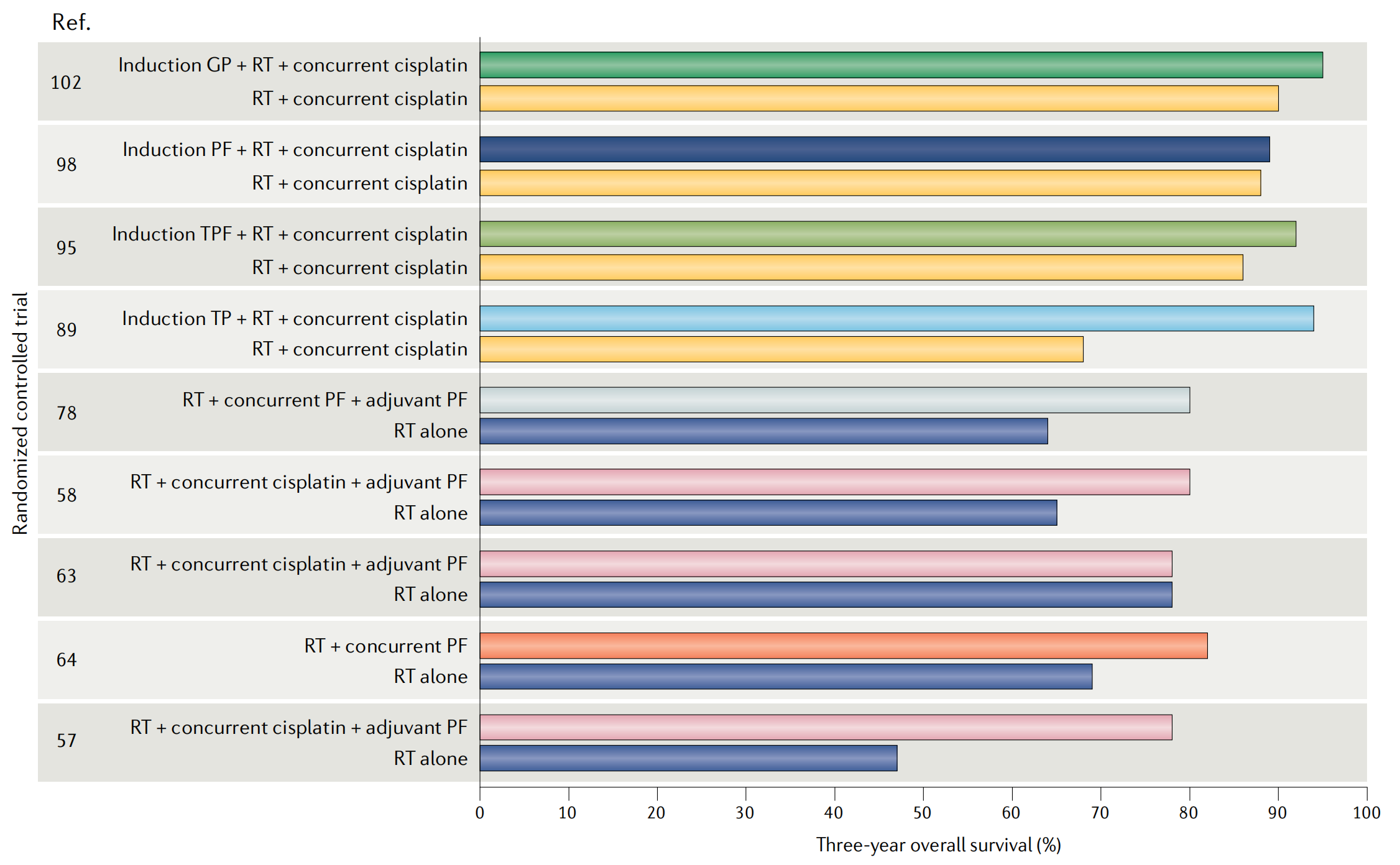
在Web UI中打开一个图像文件,然后点击[Submit]按钮,就可以进行检测,如下图所示:
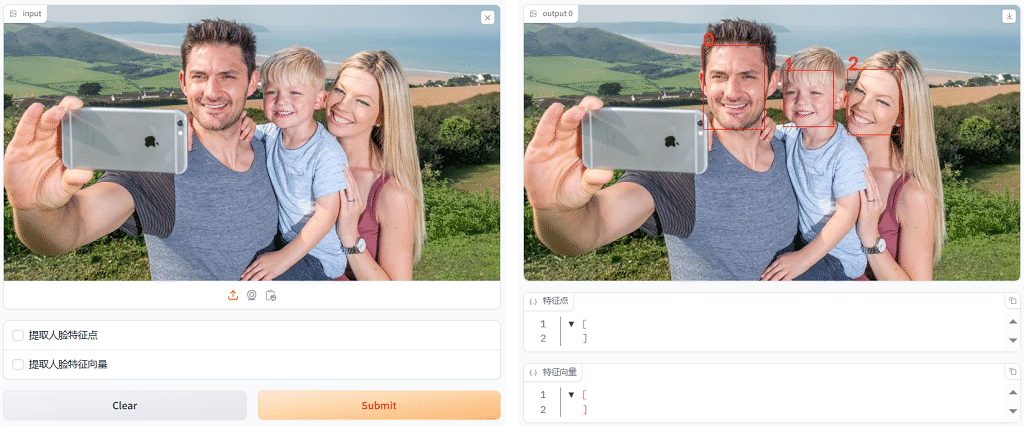
选中 提取人脸特征点 ,然后点击[Submit]按钮,可以提取人脸特征点(68点),如下图所示:
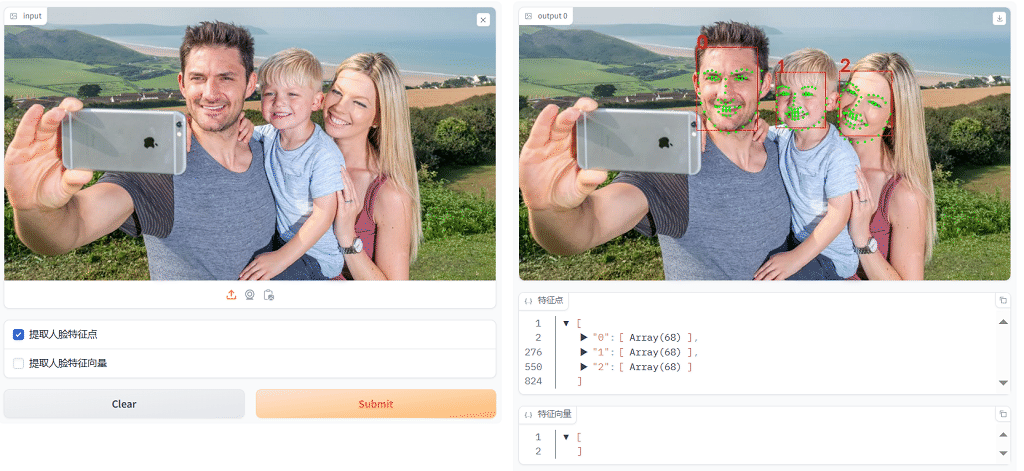
选中 提取人脸特征向量 ,然后点击[Submit]按钮,可以提取人脸特征向量(512维),如下图所示:
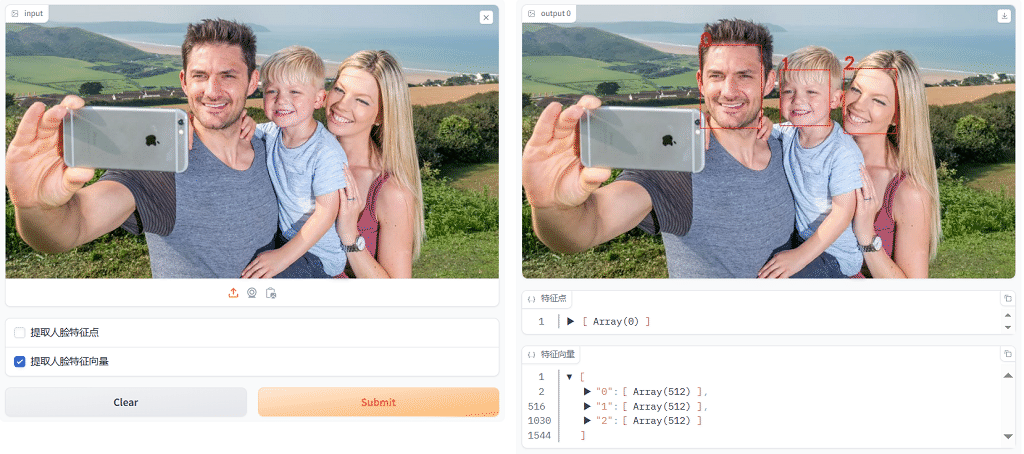
3、使用Web API
访问端点: /predict
输入参数:
input:输入图像extract_landmark:是否提取人脸特征点extract_embedding:是否提取人脸特征向量
输出结果:
[0]:输出图像文件路径[1]:人脸特征点数组[2]:人脸特征向量数组
Python调用示例如下:
from gradio_client import Client, handle_file
client = Client("http://127.0.0.1:7860/")
result = client.predict(
input=handle_file('./samples/test-1.jpg'),
extract_landmark=True,
extract_embedding=True,
api_name="/predict"
)
print(result)
执行结果如下:
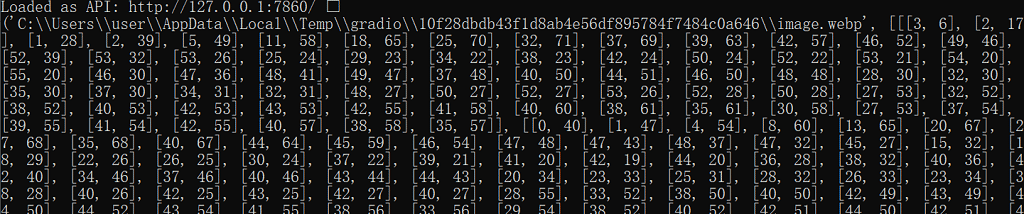
4、使用原生API
除了Web API,Face2V SDK也提供了Python原生API。
4.1 人脸检测器
FaceDetector是人脸检测器类,使用其 process()方法对传入的图片进行处理,并返回检测结果数据。
FaceDetector实例的 process()调用示例代码如下:
from core import FaceDetector # 导入FaceDetector
import cv2
fd = FaceDetector() # 实例化FaceDetector
input = cv2.imread('samples/selfie-1.jpg') # 读取输入的包含人脸的图片
boxes, probs = fd.process(input) # 返回检测到的人脸包围盒及对应的概率
for box in boxes: # 遍历所有包围盒
x1, y1, x2, y2 = box
print(f'face in rect => {(x1,y1)}, {(x2,y2)}') # 输出包围盒的两个顶点坐标
4.2 特征点回归器
LandmarkRegressor是人脸特征点回归器,使用其 process()方法提取传入人脸图片的68个特征点:
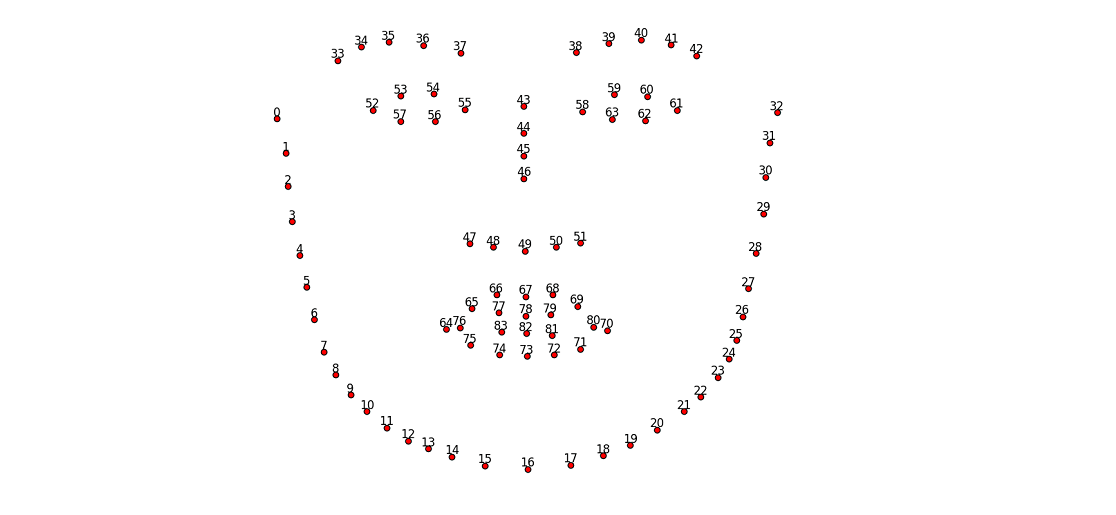
LandmarkRegressor实例的 process()调用示例代码如下:
from core import LandmarkRegressor # 导入LandmarkRegressor
import cv2
lr = LandmarkRegressor() # 实例化LandmarkRegressor
input = cv2.imread('samples/f0.jpg') # 读取输入的人脸图片
landmark = lr.process(input) # 提取输入人脸图片的特征点
for i, xy in enumerate(landmark): # 遍历所有特征点
print(f'{i}: {xy}') # 输出每个特征点的序号和x, y坐标
4.3 特征向量提取器
EmbeddingExtractor是人脸特征向量提取器,使用其 process()方法提取传入人脸图片的512维向量, 可用于人脸搜索等应用。
EmbeddingExtractor实例的 process()调用示例代码如下:
from core import EmbeddingExtractor # 导入EmbeddingExtractor
import cv2
ee = EmbeddingExtractor() # 实例化EmbeddingExtractor
input = cv2.imread('samples/f0.jpg') # 读取输入的人脸图像
embedding = ee.process(input) # 返回对应的512维特征向量
print(f'embedding => {embedding}') # 打印输出特征向量y原文链接:Face2V人脸向量开发包 - 汇智网