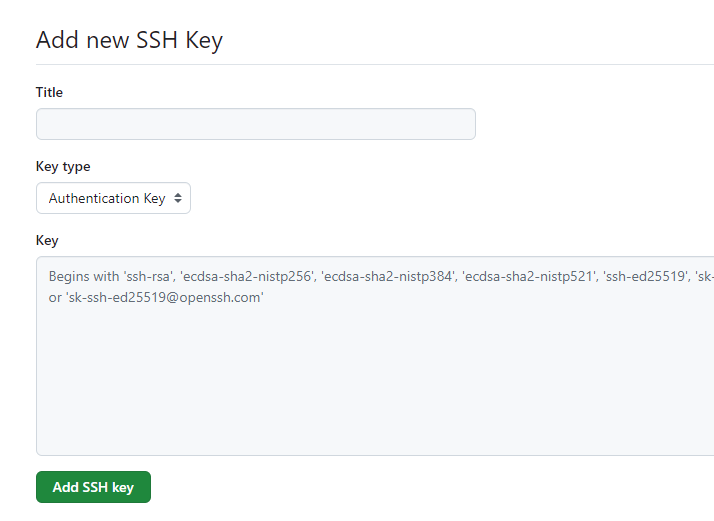
多段 线 数据压缩 （200）

• 如图中每个方格为一个像素（i，j），线的走向只能水平、垂直、倾斜45度；
• 图中线段表示为(2, 8)、（3,7）、（3, 6）、（3，5）、（4, 4）、（5， 3）、（6, 2）、（7, 3）、（8，4）、（7，5）
• 该线段可以压缩为(2, 8)、（3,7）、（3，5）、（6, 2）、（8，4）、（7，5）, 分别为起点、拐点、终点
• 根据输入的线段数据，输出简化的结果
  

输入描述：
2 8 3 7 3 6 3 5 4 4 5 3 6 2 7 3 8 4 7 5
每两个一组（i, j） i,j 范围为【0,64】
输入至少包含两个坐标点
输出描述：
2 8 3 7 3 5 6 2 8 4 7 5

思路：

• 每次取三个点，形成两个向量v1, v2
• 计算v1,v2的余弦值cos，值为 1/-1 时共线，共线时 记录删除中间点的索引
• 注意python无法精确表示小数，避免开根号

s = input().strip()
n = len(s)

# 字符串转为点
points = []
remove_points = []
for i in range(0, n, 4):
    points.append(list(map(int, s[i:i+4].strip().split())))


def inline(v1, v2):
    a = 0
    v1_sum = 0
    v2_sum = 0
    # 计算内积
    for j in range(2):
        a += v1[j] * v2[j]
        v1_sum += v1[j]**2
        v2_sum += v2[j]**2

    b = v1_sum * v2_sum # 开根号 无法精确表示小数，所有分子分母均平方
    if a**2 == b:  # 余弦值为1，夹角为0 或者180  共线
        return True

    return False


#
# [[2, 8], [3, 7], [3, 6], [3, 5], [4, 4], [5, 3], [6, 2], [7, 3], [8, 4], [7, 5]]
point_num = len(points)
for i in range(point_num-2): # 每次取三个点，形成两个向量，计算是否共线 (只需关心是否为拐点)
    v1 = [points[i][0]-points[i+1][0], points[i][1]-points[i+1][1]]
    v2 = [points[i+1][0]-points[i+2][0], points[i+1][1]-points[i+2][1]]
    if inline(v1, v2): # 如果共线，则记录删除中间点 即 i+1 位置
        remove_points.append(i+1)


print("删除点", remove_points)

# 遍历所有的坐标点
out_str = ""
for j in range(point_num):
    if j not in remove_points:
        s, e = points[j]
        out_str += str(s) + " " + str(e) + " "

print(out_str.strip())