LRU缓存介绍
什么是LRU缓存?
LRU缓存是一种缓存策略,当缓存满了,需要腾出空间存放新数据时,它会删除最近最少使用的数据。换句话说,它会优先淘汰那些最久没有被访问的元素,以确保缓存中的数据是最近使用的,这对提高缓存系统的命中率有帮助。
让我们通过一个例子来理解LRU
假设内存中有5个远端,缓存的大小为 3.
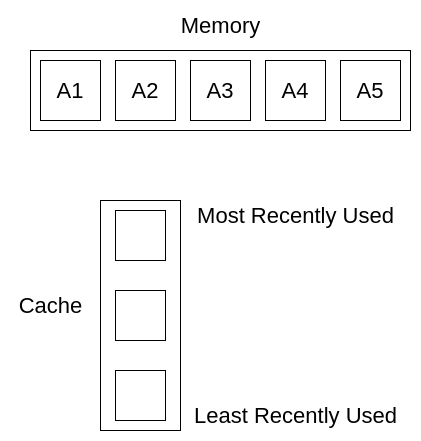
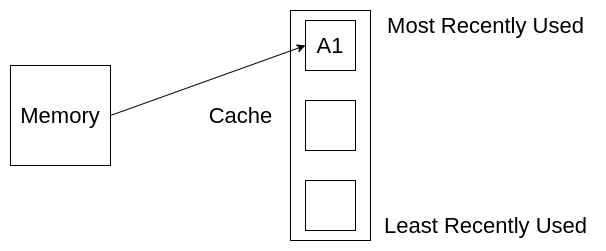
最初缓存是空的,所有元素都存在内存中,我们先访问内存中元素A1,并将其放入缓存中。
接下来,我们访问内存中的元素A2将其放入缓存,A2存储在 最顶端,此时,缓存中的A1下移,因为A1不再是最近访问的元素了。
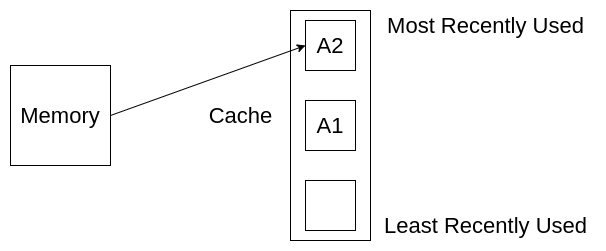
接下来,我们访问内存中的元素A3,过程与访问A2类似,此时A3位于缓存顶端,A1,A2下移。
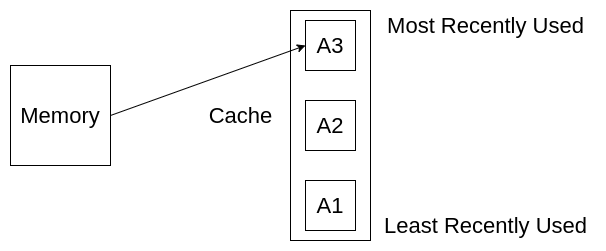
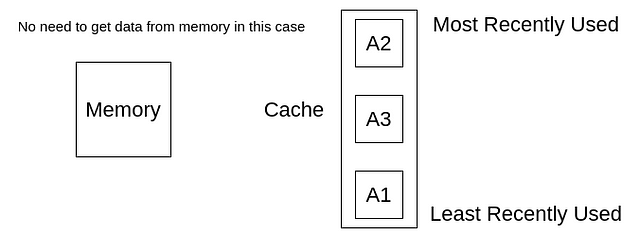
现在,我们再次访问A2,我们可以从缓存中获取了,而不是从内存中获取,但是需要注意的是,获取到A2之后,需要将A2移动到缓存的顶部,因为A2是目前最近访问过的元素。
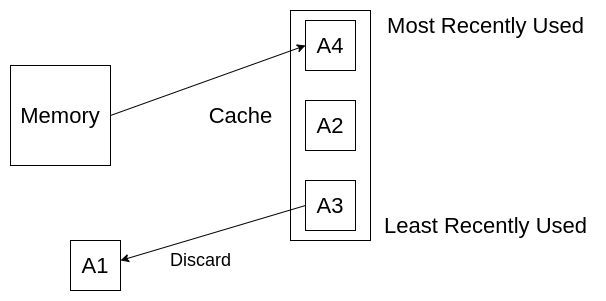
现在,我们访问A4,我们必须从内存中获取它,但是我们将它放到缓存中的哪个位置了,现在缓存已经满了,我们必须删除一些元素以便容纳A4,在本例中,我们删除了最近最少使用的A1,这就是最近最少使用(LRU)算法。
LRU缓存实现
如何设计一个LRU缓存:
如何设计一个支持以下操作的LRU缓存:
- LRUCache(int capacity):初始化LRU缓存,并设定缓存的容量。
- int get(int key):如果key存在于缓存中,返回它对应的value;如果不存在,返回-1。
- void put(int key, int value):如果key已经在缓存中,更新它的value;如果key不在缓存中,将新的key-value对加入缓存。如果缓存满了,需要先移除最近最少使用的元素,再插入新的key-value对。
要求:
- 访问和更新缓存中的元素,时间复杂度为O(1)。
- 删除缓存中最久未使用的元素,时间复杂度也为O(1)。
方式一:使用数组实现LRU缓存
使用一个固定大小的数组存储缓存中的元素,每个元素除了存储key和value外,还存储一个时间戳timeStamp,标记元素的访问时间。当我们访问或插入一个元素时,更新该元素的时间戳,以表示它是最近使用过的。当缓存满时,我们需要找到时间戳最大的元素(表示最久未使用),将其删除,然后插入新元素。
class DataElement {
int key;
int value;
int timeStamp;
public DataElement(int k, int data, int time) {
key = k;
value = data;
timeStamp = time;
}
}
这种方式的问题是:
- 每次访问元素需要遍历数组,这个时间复杂度为O(n)。
- 如果缓存已满需要为新元素腾出空间时,需要遍历数组找到最久未使用的元素。这个时间复杂度为O(n),非常低效。
方式二:使用单链表实现LRU缓存
使用单链表存储缓存中的元素,链表头部是最近使用的元素,尾部是最久未使用的元素。每次访问或插入元素时,将该元素移到链表头部。
这种方式get和put操作的时间复杂度都是O(n):
- 从缓存中获取指定元素时,需要遍历链表,时间复杂度是O(n)。
- 插入元素到缓存中,如果缓存已满,需要删除最近最少使用的 缓存,也就是尾部的元素,为此,需要遍历链表到达末尾,时间复杂度也是O(n)。
方式三:使用哈希表和双向链表实现LRU缓存
我们需要结合双向链表和哈希表来实现LRU缓存。
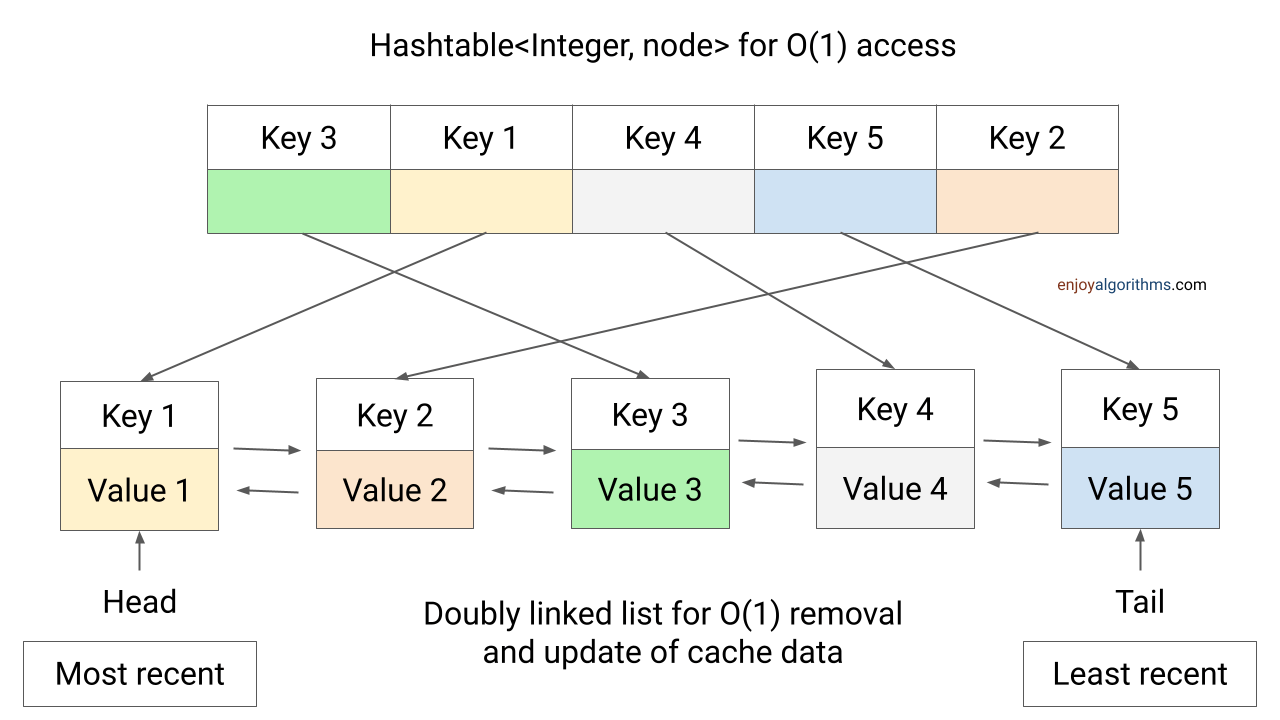
查找元素
详细步骤:
- 在哈希表中查找是否存在该key。
- 如果存在,表示缓存命中(cache hit),我们将对应的节点移动到链表头部(表示它是最近使用的元素)。
- 如果不存在,返回-1,表示缓存未命中(cache miss)。
插入元素
- 先查找哈希表,判断key是否已经存在。
- 如果存在,更新其value,并将对应节点移到链表头部。
- 如果不存在,检查缓存是否已满,如果未满,将新元素插入链表头部,并在哈希表中记录。
- 如果已满,删除链表尾部的最久未使用元素(同时删除哈希表中的对应记录),然后插入新元素到链表头部。
下面是一个LRU缓存的Java实现:
public class LRUCache {
class Node {
int key;
int value;
Node pre;
Node post;
}
private Hashtable<Integer, Node> cache = new Hashtable<Integer, Node>();
private int count;
private int capacity;
private Node head, tail;
// Add the new node right after head
private void addNode(Node node) {
node.pre = head;
node.post = head.post;
head.post.pre = node;
head.post = node;
}
// Remove an existing node from the linked list
private void removeNode(Node node) {
Node pre = node.pre;
Node post = node.post;
pre.post = post;
post.pre = pre;
}
// Move node in between to the head
private void moveToHead(Node node) {
removeNode(node);
addNode(node);
}
// Pop the current tail
private Node popTail() {
Node res = tail.pre;
removeNode(res);
return res;
}
public LRUCache(int capacity) {
this.count = 0;
this.capacity = capacity;
head = new Node();
head.pre = null;
tail = new Node();
tail.post = null;
head.post = tail;
tail.pre = head;
}
public int get(int key) {
Node node = cache.get(key);
if (node == null) {
return -1;
}
moveToHead(node);
return node.value;
}
public void put(int key, int value) {
Node node = cache.get(key);
if (node == null) {
Node newNode = new Node();
newNode.key = key;
newNode.value = value;
cache.put(key, newNode);
addNode(newNode);
++count;
if (count > capacity) {
// Pop the tail
Node tailNode = popTail();
cache.remove(tailNode.key);
--count;
}
} else {
// Update the value.
node.value = value;
moveToHead(node);
}
}
}