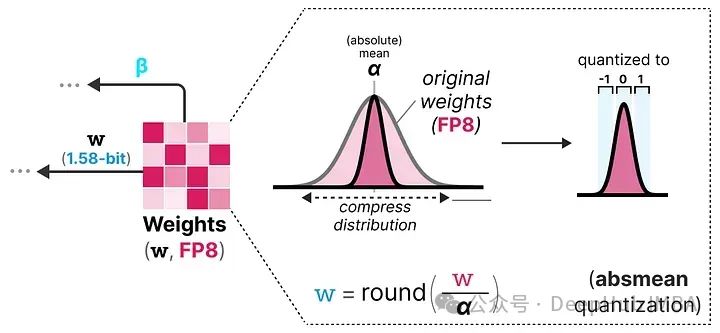
目录

1.可积和有界的关系

2.连续和可积的关系

3.连续和存在原函数的关系

4.可积和存在原函数没有关系

---

1.可积和有界的关系

可积必有界，有界不一定可积，反例可以举狄利克雷函数

2.连续和可积的关系

f(x)连续，则一定可积，可积不一定连续

参考两种定义：

① 若f(x)在[a,b]上仅有有限个第一类间断点，则一定可积。

② 若f(x)在[a,b]上有界且只有有限个间断点，则一定可积。

如果参考第②条定义，那么若有第二类间断点也可能是可积的（不可能为无穷间断点）。但这里并没有找到合适的举例 

3.连续和存在原函数的关系

该知识点对应张宇30讲p138，也可以看下面的反例：

f(x)连续一定存在原函数，但是f(x)存在原函数不能推出f(x)连续，参考下面的举例，f(x)有振荡间断点，但是f(x)有原函数。

4.可积和存在原函数没有关系

（1）可积但不存在原函数

（2）存在原函数但不可积

（3）既不可积也不存在原函数

总结：

f(x)存在原函数和f(x)可积并没有关系，连续是最强的条件，f(x)连续则一定可积，f(x)连续则一定存在原函数。

注意与变上限积分区别：

变上限积分说的是，f(x)在[a,b]上可积，则f(x)的变上限积分在[a,b]连续。

我们知道，f(x)有有限个第一类间断点，那么f(x)是可积的（f(x)的定积分存在）。若函数含有第一类间断点，其变上限积分函数的可导性：

f(x)和F(x)的关系是什么：

① 若f(x)在x=x0处连续，那么

② 若f(x)在x=x0处为可去间断点，那么

F(x)可导，不等于这一点f(x)的函数值，而是f(x)的极限值

③ 若f(x)在x=x0处为跳跃间断点，那么

F(x)连续（f(x)可积，F(x)就连续）但不可导，且：

所以变上限积分一定是f(x)的原函数这句话是错的，应该说，f(x)连续，则变上限积分一定是f(x)的原函数。（若f(x)某点是可去间断点，那么F(x)可导，但是并不等于这点的函数值）

我们可以总结这样一个规律，通俗一点讲：

f(x)做积分后，性质就变好了，例如：

f(x)在[a,b]上可积（不一定连续，可有有限个第一类间断点），那么F(x)在[a,b]上连续。

f(x)在[a,b]上连续，那么F(x)在[a,b]上可导。

f(x)求导性质就变差了，例如：

f(x)可导，但是f ‘ (x)都不一定连续。

---

对于易混淆的概念，我有一篇文章进行了总结，需要可以看看：

考研数学经典反例