C++ 最小生成树 洛谷

news2024/11/15 7:18:43

介绍：

最小生成树是个啥？其实就像杨志一行人押送生辰纲。抛开最后生辰纲被抢的结局不谈，杨志他们需要到好几个地方，每个地方都需要花点过路费给梁山好汉们打点。比如下面就是一张城市地图：

地图

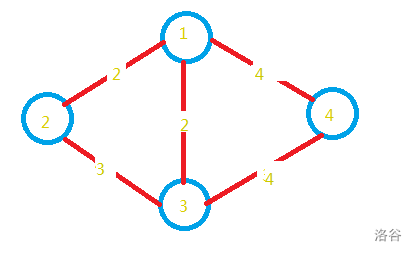
其中每两个图之间的路径长就是要给梁山好汉们打点的银子数。比如1号地点到2号地点的梁山好汉需要2两银子。那么问题来了，怎样才能选择其中一部分道路就可以到达所有地点且让总花费值最小呢？？？

如果有n个节点（城市），那就至少要连（n-1）条边（路线），并且肯定没有回路。（不信？画几个图试试）众所周知，在无向图中，只要这个图里没有回路（有（n-1）条边），那它就无疑是棵树了。（还是不信？画图......）所以，**我们就管这棵各边权值（费用）和叫“最小生成树”**了。

那这个最小生成树到底怎么搞呢？我们伟大的先哲发明了两种算法：一种叫Kruskal算法，另一种叫Prim算法。我们这里就来介绍一下名字字典序靠前的那个Kruskal吧！（我才不会告诉你根本原因是本蒟蒻不会用Prim呢！）

那咱就开始吧！首先，我们读入的数据是这样的！

1 2 2
1 3 2
1 4 4
2 3 3
3 4 4

其中每一行的a,b,c 3个数是指a到b的路径权值是c哦！

既然题目中让我们求“最小”生成树，那咱们就自然而然地想到先把这些边排个序，先用最小的边，从小到大一路把这棵树搞出来！

说干就干，排一个呗！

1 2 2
1 3 2 
2 3 3
1 4 4
3 4 4

排好之后，映入我们眼帘的是“1，2，2”这条边，二话不说，把它放到生成树里！

过程1

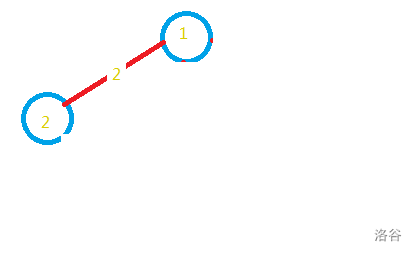
接下来是“1，2，2”，很好，把它也加进去

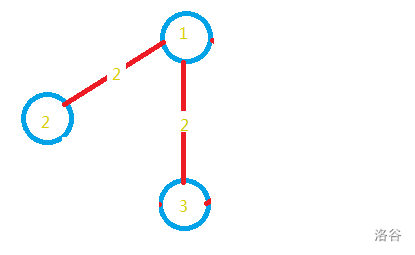
然后是“2，3，3”，好多同学把它都加了进去......

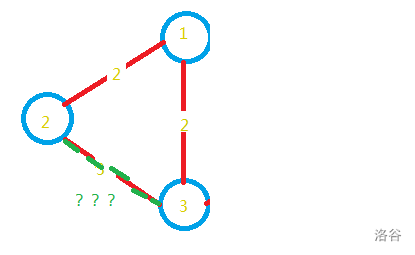
等会等会，先别忙着加！好像有什么猫腻！前面说过，最小生成树，是不能带回路的，加进去一不是最小，二它连个树都不是，所以不能加！于是我们意识到：在每次加进去新边之前，一定要看看它和其它边会不会构成回路才行！

那咱就只能退而求其次，选其它的边啦，“1，4，4”这可不是回路，没问题！

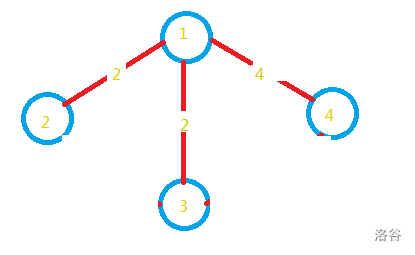
至此，边数已达（n-1）条，所有点已经选上，最小生成树大功告成！（当然，选下面的“3，4，4”也是阔以的）

总结一下，我们刚才是怎样搞出这棵最小生成树的：

  1. 把边们从小到大排个序
  2. 如果没有回路，一条一条往里加
  3. 边数达到（n-1）条，完成

步骤都弄懂啦！但是这个“回路”到底怎么判断呢？

所谓判断回路，就是看看有了这条边之后，有没有连通的部分，从“树”的角度来看，就是两个点的根节点（也就是“祖宗”）是不是一样的

哎？话说说到这里，诸位有没有联想到什么啊？

没错，就是金光闪闪的并！查！集！

并查集是啥就不在我的责任范围之内啦，（其实就是懒癌犯了）这里我就默认泥萌都会并查集了......

所以说我们可以搞个并查集出来，然后每加入条边时，先用并查集的“查询”功能，看看两个节点的祖宗是不是一样的，如果不一样就把他俩“合并”，就可以放心大胆的往里加啦~

P3366 【模板】最小生成树

题目描述

如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出 orz。

输入格式

第一行包含两个整数 N,M，表示该图共有 N 个结点和 M 条无向边。

接下来 M 行每行包含三个整数 Xi,Yi,Zi​，表示有一条长度为 Zi​ 的无向边连接结点 Xi,Yi​。

输出格式

如果该图连通，则输出一个整数表示最小生成树的各边的长度之和。如果该图不连通则输出 orz。

#include<bits/stdc++.h>
#define int long long
#define PII pair<int,int >
#define fi first
#define se second
#define pb push_back
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)

using namespace std;

const int N = 1e6+10;

int n,m;
int acc[N];

pair<int,pair<int,int>> va[N];

int find(int x)
{
	if(acc[x]!=x) acc[x] = find(acc[x]);
	return acc[x];
}

void krukal()
{
	int cnt = 0,sum = 0;
	for(int i = 1;i<=n;i++) acc[i] = i;
	for(int i = 1;i<=m;i++)
	{
		int a = va[i].se.fi,b = va[i].se.se,c = va[i].fi;
		int t1 = find(a),t2 = find(b);
		if(t1!=t2)
		{
			acc[t1] = t2;
			sum += c;
			cnt++;
		}
	}
	if(cnt==n-1) cout<<sum;
	else cout<<"orz";
}

signed main()
{
	IOS;
	cin>>n>>m;
	for(int i = 1;i<=m;i++)
	{
		int a,b,c;
		cin>>a>>b>>c;
		va[i] = {c,{a,b}};
	}
	sort(va+1,va+1+m);
	krukal();
	return 0;
}

P2330 [SCOI2005] 繁忙的都市

题目描述

城市 C 是一个非常繁忙的大都市，城市中的道路十分的拥挤，于是市长决定对其中的道路进行改造。城市 C 的道路是这样分布的：城市中有 nn 个交叉路口，有些交叉路口之间有道路相连，两个交叉路口之间最多有一条道路相连接。这些道路是双向的，且把所有的交叉路口直接或间接的连接起来了。每条道路都有一个分值，分值越小表示这个道路越繁忙，越需要进行改造。但是市政府的资金有限，市长希望进行改造的道路越少越好，于是他提出下面的要求：

  1. 改造的那些道路能够把所有的交叉路口直接或间接的连通起来。
  2. 在满足要求 1 的情况下，改造的道路尽量少。
  3. 在满足要求 1、2 的情况下，改造的那些道路中分值最大的道路分值尽量小。

任务：作为市规划局的你，应当作出最佳的决策，选择哪些道路应当被修建。

输入格式

第一行有两个整数 n,m 表示城市有 n 个交叉路口，m 条道路。

接下来 m 行是对每条道路的描述，u,v,c 表示交叉路口 u 和 v 之间有道路相连，分值为 c。

输出格式

两个整数 s,max，表示你选出了几条道路，分值最大的那条道路的分值是多少。

#include<bits/stdc++.h>
#define int long long
#define PII pair<int,int >
#define fi first
#define se second
#define pb push_back
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)

using namespace std;

const int N = 1e6+10;

int n,m;
int acc[N];

pair<int,pair<int,int>> va[N];

int find(int x)
{
	if(acc[x]!=x) acc[x] = find(acc[x]);
	return acc[x];
}

void krukal()
{
	int cnt = 0,sum = 0;
	for(int i = 1;i<=n;i++) acc[i] = i;
	for(int i = 1;i<=m;i++)
	{
		int a = va[i].se.fi,b = va[i].se.se,c = va[i].fi;
		int t1 = find(a),t2 = find(b);
		if(t1!=t2)
		{
			acc[t1] = t2;
			cnt++;
		}
		if(cnt==n-1) 
		{
			cout<<cnt<<" "<<c;
			break;
		}
	}
	
}

signed main()
{
	IOS;
	cin>>n>>m;
	for(int i = 1;i<=m;i++)
	{
		int a,b,c;
		cin>>a>>b>>c;
		va[i] = {c,{a,b}};
	}
	sort(va+1,va+1+m);
	krukal();
	return 0;
}

P1195 口袋的天空

题目背景

小杉坐在教室里，透过口袋一样的窗户看口袋一样的天空。

有很多云飘在那里，看起来很漂亮，小杉想摘下那样美的几朵云，做成棉花糖。

题目描述

给你云朵的个数 N，再给你 M 个关系，表示哪些云朵可以连在一起。

现在小杉要把所有云朵连成 K 个棉花糖，一个棉花糖最少要用掉一朵云，小杉想知道他怎么连，花费的代价最小。

输入格式

第一行有三个数 N,M,K。

接下来 M 行每行三个数 X,Y,L，表示 X 云和 Y 云可以通过 L 的代价连在一起。

输出格式

对每组数据输出一行，仅有一个整数，表示最小的代价。

如果怎么连都连不出 K 个棉花糖，请输出 No Answer。

题解：

首先让我们选k朵云做棉花糖，换句话说就是选k个节点构造最小生成树，那不好办！我们都知道，全部n个点的最小生成树有（n-1）条边，那选k个节点就是（n-k）条边呗！

其次就是这个“No Answer”怎么弄的问题，其实也so easy，你想啊，一共就m条边，如果都选完了还没有选出（n-k）条边来，那就是妥妥的No Answer 了

说了这么多，是时候放代码了！听我这么一讲解，大家应该都理解最小生成树的Kruskal算法了吧！

#include<bits/stdc++.h>
#define int long long
#define PII pair<int,int >
#define fi first
#define se second
#define pb push_back
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)

using namespace std;

const int N = 1e5+10;

int n,m,k;
int acc[N];

pair<int,pair<int,int>> va[N];

int find(int x)
{
	if(acc[x]!=x) acc[x] = find(acc[x]);
	return acc[x];
}

void krukal()
{
	int cnt = 0,sum = 0;
	for(int i = 1;i<=n;i++) acc[i] = i;
	for(int i = 1;i<=m;i++)
	{
		int a = va[i].se.fi,b = va[i].se.se,c = va[i].fi;
		int t1 = find(a),t2 = find(b);
		if(t1!=t2)
		{
			acc[t1] = t2;
			cnt++;
			sum += c;
		}
		if(cnt==n-k) break;
	}
	if(cnt==n-k) cout<<sum;
	else cout<<"No Answer";
}

signed main()
{
	IOS;
	cin>>n>>m>>k;
	for(int i = 1;i<=m;i++)
	{
		int a,b,c;
		cin>>a>>b>>c;
		va[i] = {c,{a,b}};
	}
	sort(va+1,va+1+m);
	krukal();
	return 0;
}

P1547 [USACO05MAR] Out of Hay S

题目描述

Bessie 计划调查 N（2≤N≤2 000）个农场的干草情况，它从 1 号农场出发。农场之间总共有 M（1≤M≤104）条双向道路，所有道路的总长度不超过 109。有些农场之间存在着多条道路，所有的农场之间都是连通的。

Bessie 希望计算出该图中最小生成树中的最长边的长度。

输入格式

第一行两个整数 N,M。

接下来 M 行，每行三个用空格隔开的整数 Ai,Bi,Li，表示 Ai,Bi 之间有一条道路，长度为 Li​。

输出格式

一个整数，表示最小生成树中的最长边的长度。

#include<bits/stdc++.h>
#define int long long
#define PII pair<int,int >
#define fi first
#define se second
#define pb push_back
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)

using namespace std;

const int N = 1e6+10;

int n,m;
int acc[N];

pair<int,pair<int,int>> va[N];

int find(int x)
{
	if(acc[x]!=x) acc[x] = find(acc[x]);
	return acc[x];
}

void krukal()
{
	int cnt = 0,sum = 0;
	for(int i = 1;i<=n;i++) acc[i] = i;
	for(int i = 1;i<=m;i++)
	{
		int a = va[i].se.fi,b = va[i].se.se,c = va[i].fi;
		int t1 = find(a),t2 = find(b);
		if(t1!=t2)
		{
			acc[t1] = t2;
			cnt++;
			sum += c;
		}
		if(cnt==n-1) 
		{
			cout<<c;
			break;
		}
	}
}

signed main()
{
	IOS;
	cin>>n>>m;
	for(int i = 1;i<=m;i++)
	{
		int a,b,c;
		cin>>a>>b>>c;
		va[i] = {c,{a,b}};
	}
	sort(va+1,va+1+m);
	krukal();
	return 0;
}

P2872 [USACO07DEC] Building Roads S

题目描述

给定 n 个点的坐标，第 i 个点的坐标为 (xi,yi)，这 n 个点编号为 1 到 n。给定 m 条边，第 i 条边连接第 ui​ 个点和第 vi​ 个点。现在要求你添加一些边，并且能使得任意一点都可以连通其他所有点。求添加的边的总长度的最小值。

输入格式

第一行两个整数 n,m 代表点数与边数。
接下来 n 行每行两个整数 xi​,yi​ 代表第 i 个点的坐标。
接下来 m 行每行两个整数 ui,vi 代表第 i 条边连接第 ui​ 个点和第 vi​ 个点。

输出格式

一行一个实数代表添加的边的最小长度，要求保留两位小数，为了避免误差， 请用 64 位实型变量进行计算。

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define pb push_back
#define fi first
#define int long long
#define pii pair<int,int >
#define se second

using namespace std;

const int N=2e6+10;
int acc[N];
int n,m;

struct node
{
	int u,v;
	double w;
}va[N];

struct Node
{
	int x,y;
}vb[N];

bool cmp(node a,node b)
{
	if(a.w!=b.w) return a.w<b.w;
}

int find(int x)
{
	if(acc[x]!=x) acc[x]=find(acc[x]);
	return acc[x];
}

signed main()
{
	IOS;
	cin>>n>>m;	
	int sum=0;
	double sum1 = 0.0;
	for(int i=1;i<=n;i++)
	{
		cin>>vb[i].x>>vb[i].y;
	}
	for(int i=1;i<=n;i++) acc[i]=i;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			sum++;
			va[sum].u=i;
			va[sum].v=j;
			va[sum].w=sqrt(pow(vb[i].x-vb[j].x,2)+pow(vb[i].y-vb[j].y,2));
		}
	}
	for(int i=1;i<=m;i++)
	{
		sum++;
		int a,b;
		cin>>a>>b;
		va[sum].u=a;
		va[sum].v=b;
		va[sum].w=0.0;
	}
	sort(va+1,va+1+sum,cmp);
	int cnt = 0;
	for(int i=1;i<=n*n;i++)
	{
		if(find(va[i].u)!=find(va[i].v))
		{
			acc[find(va[i].u)]=find(va[i].v);
			sum1+=va[i].w;
			cnt++;
		}
		else continue;
		if(cnt==n-1) printf("%.2lf",sum1);
	}
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1977178.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【保姆级系列：锐捷模拟器的下载安装使用全套教程】

【保姆级系列：锐捷模拟器的下载安装使用全套教程】

保姆级系列&#xff1a;锐捷模拟器的下载安装使用全套教程 1.介绍2.下载3.安装4.实践教程5.验证 1.介绍 锐捷目前可以通过EVE-NG来模拟自己家的路由器&#xff0c;交换机&#xff0c;防火墙。实现方式是把自己家的镜像导入到EVE-ng里面来运行。下面主要就是介绍如何下载镜像和…
阅读更多...
【Unity】3D功能开发入门系列（三）

【Unity】3D功能开发入门系列（三）

Unity3D功能开发入门系列&#xff08;三&#xff09; 一、运动脚本&#xff08;一&#xff09;物体的运动&#xff08;二&#xff09;相对运动&#xff08;三&#xff09;运动的方向 二、旋转脚本&#xff08;一&#xff09;物体的旋转&#xff08;二&#xff09;相对旋转&…
阅读更多...
图像相关的基础知识【RGB和RGBA】—附python代码实现

图像相关的基础知识【RGB和RGBA】—附python代码实现

文章目录 1、图像基础知识2、像素和通道的理解3、RGB和RGBARGB (Red, Green, Blue)RGBA (Red, Green, Blue, Alpha)应用场景 4、H,W,C5、小结 &#x1f343;作者介绍&#xff1a;双非本科大三网络工程专业在读&#xff0c;阿里云专家博主&#xff0c;专注于Java领域学习&#x…
阅读更多...
aurora8b10b ip的使用（framing接口下的数据回环测试）

aurora8b10b ip的使用（framing接口下的数据回环测试）

文章目录 一、Aurora8B/10B协议二、时钟、复位与状态指示1、时钟2、复位3、状态指示 三、数据发送、接受接口&#xff08;1&#xff09;AXI4-Stream位排序&#xff08;2&#xff09;Streaming接口&#xff08;3&#xff09;Framing接口&#xff08;帧传输接口&#xff09; 四、…
阅读更多...
C++ | Leetcode C++题解之第319题灯泡开关

C++ | Leetcode C++题解之第319题灯泡开关

题目&#xff1a; 题解&#xff1a; class Solution { public:int bulbSwitch(int n) {return sqrt(n 0.5);} };
阅读更多...
Python | Leetcode Python题解之第318题最大单词长度乘积

Python | Leetcode Python题解之第318题最大单词长度乘积

题目&#xff1a; 题解&#xff1a; class Solution:def maxProduct(self, words: List[str]) -> int:masks defaultdict(int)for word in words:mask reduce(lambda a, b: a | (1 << (ord(b) - ord(a))), word, 0)masks[mask] max(masks[mask], len(word))return…
阅读更多...
索引：SpringCloudAlibaba分布式组件全部框架笔记

索引：SpringCloudAlibaba分布式组件全部框架笔记

索引&#xff1a;SpringCloudAlibaba分布式组件全部框架笔记 一推荐一套分布式微服务的版本管理父工程pom模板&#xff1a;Springcloud、SpringCloudAlibaba、Springboot二SpringBoot、SpringCloud、SpringCloudAlibaba等各种组件的版本匹配图&#xff1a;三SpringBoot 3.x.x版…
阅读更多...
字符串相关函数

字符串相关函数

文章目录 &#x1f34a;自我介绍&#x1f34a;strcpy 字符串拷贝函数&#x1f34a;strcat 字符串连接函数&#x1f34a;strlen 字符串长度计算函数&#x1f34a;strcmp 字符串比较函数 你的点赞评论就是对博主最大的鼓励 当然喜欢的小伙伴可以&#xff1a;点赞关注评论收藏&…
阅读更多...
C++ | Leetcode C++题解之第318题最大单词长度乘积

C++ | Leetcode C++题解之第318题最大单词长度乘积

题目&#xff1a; 题解&#xff1a; class Solution { public:int maxProduct(vector<string>& words) {unordered_map<int,int> map;int length words.size();for (int i 0; i < length; i) {int mask 0;string word words[i];int wordLength word.s…
阅读更多...
[Git][基本操作]详细讲解

[Git][基本操作]详细讲解

目录 1.创建本地仓库2.配置 Git3.添加文件1.添加文件2.提交文件3.其他 && 说明 4.删除文件5.跟踪修改文件6.版本回退7.撤销修改0.前言1.未add2.已add&#xff0c;未commit3.已add&#xff0c;已commit 1.创建本地仓库 创建⼀个Git本地仓库&#xff1a;git init运行该命…
阅读更多...
模型 ESBI（财富四象限）

模型 ESBI（财富四象限）

系列文章 分享 模型&#xff0c;了解更多&#x1f449; 模型_思维模型目录。财富自由之路的4个阶段。 1 ESBI模型的应用 1.1 一名工程师的财富自由之路 有一个名叫张伟的软件工程师&#xff0c;他在一家大型科技公司工作&#xff08;E象限&#xff09;。随着时间的推移&#…
阅读更多...
模型量化技术综述：揭示大型语言模型压缩的前沿技术

模型量化技术综述：揭示大型语言模型压缩的前沿技术

大型语言模型&#xff08;LLMs&#xff09;通常因为体积过大而无法在消费级硬件上运行。这些模型可能包含数十亿个参数&#xff0c;通常需要配备大量显存的GPU来加速推理过程。 因此越来越多的研究致力于通过改进训练、使用适配器等方法来缩小这些模型的体积。在这一领域中&am…
阅读更多...
electron-updater实现electron全量更新和增量更新——渲染进程交互部分

electron-updater实现electron全量更新和增量更新——渲染进程交互部分

同学们可以私信我加入学习群&#xff01; 正文开始 前言更新功能所有文章汇总一、监听页面渲染完毕1.1 myApi.handleCheckPcUpdate检查更新1.2myApi.onPcUpdateProgress接收下载信息1.3myApi.onPcDownloaded监听下载完毕事件 二、立即更新三、跳过更新四、打开更新模块总结 前言…
阅读更多...
打卡第32天------动态规划

打卡第32天------动态规划

坚持了一个月了，骑马找马，要坚持不懈呀✊ 一、动态规划理论基础 1、什么是动态规划？英文：Dynamic Programming，简称DP。 如果某一问题有很多重叠子问题，使用动态规划是最有效的。 所以动态规划中每一个状态一定是由上一个状态推导出来的，这一点就区分于贪心，贪心没有…
阅读更多...
JVM—虚拟机类加载时机与过程

JVM—虚拟机类加载时机与过程

参考资料&#xff1a;深入理解Java虚拟机&#xff1a;JVM高级特性与最佳实践&#xff08;第3版&#xff09;周志明 1. 类加载的时机 一个类型从被加载到虚拟机内存开始&#xff0c;到卸载出内存为止&#xff0c;它的生命周期会经历加载、验证、准备、解析、初始化、使用、卸载…
阅读更多...
netapp内网穿透

netapp内网穿透

1. 注册netapp账号 NATAPP-内网穿透 基于ngrok的国内高速内网映射工具 2. 购买隧道&#xff0c;要求不高的话可以使用这个免费的 3.设置隧道 主要设置你想通过公网访问你的本地端口号 4.点击我的隧道&#xff0c;注意这里的authtoken&#xff0c;后面会用到 5.本地下载netap…
阅读更多...
华中第一游戏发行平台 X 腾讯云数据库，实现IT成本降低40%

华中第一游戏发行平台 X 腾讯云数据库，实现IT成本降低40%

阅读更多...
[E二叉树] lc572. 另一棵树的子树(dfs+前中序判断+树哈希+树上KMP+好题)

[E二叉树] lc572. 另一棵树的子树(dfs+前中序判断+树哈希+树上KMP+好题)

文章目录 1. 题目来源2. 题目解析 1. 题目来源 链接&#xff1a;572. 另一棵树的子树 2. 题目解析 看到这个题目就感觉不简单&#xff0c;因为写了写 dfs 版本的&#xff0c;发现好像不太会… 还是简单粗暴一点&#xff0c;直接搞一个 前序中序&#xff0c;进行判断即可。我…
阅读更多...
应急响应-Web3

应急响应-Web3

打开虚拟机之后&#xff0c;运行解题系统&#xff1a; 共有三个问题&#xff01; 攻击者的两个IP地址 首先我们看到机器的桌面上还是存在phpstudy&#xff0c;那就还是先去看看是不是从web层面进行的攻击&#xff0c;上传webshell从而getshell。 利用D盾尝试对phpstudy目录进…
阅读更多...
Python | Leetcode Python题解之第319题灯泡开关

Python | Leetcode Python题解之第319题灯泡开关

题目&#xff1a; 题解&#xff1a; class Solution:def bulbSwitch(self, n: int) -> int:return int(sqrt(n 0.5))
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023