2023-02-01 读书笔记：《有趣的统计》-1-基础知识

75招学会数据分析 —— 2014 Doctor.Bruce Frey

序

统计学：

最初，用于确定某些事情发生的可能性；
不断发展，根据样本数据准确推断总体数据特征的方法（推论统计学）；

Hack组成（解决问题的快捷方式，也是要学习的内容点）：

使用聪明的方法解决一个统计学问题；
检验、多次回归等应用；

推论统计学（inferential statistics）是一门基于概率本质的统计科学

理解事物的运行方式，发现变量之间的相关性，透过样本分析推断出总体特征，做出预测；

统计、测量、研究设计：

第1章：基础工具集；
第2章：用于发现、描述和测量变量相关性的多种统计方法；
第3章：测量方法，正确提问，准确估算；
第4章：商用概率知识，决定胜负；
第5章：丰富的游戏技巧；
第6章：脑力游戏的探索发现；

第一章基础知识

Hack1~10

中心极限定理

样本：收集到的数值型数据；
总体：没收集到的更大的数值数据；
分数：用来表示某一特征的存在或程度的数字；
概率解释：某件事情发生可能性的解释；

概率是统计学的核心和灵魂；

基础的统计学中会教计算不同组合的出现概率或者各种可能结果排列的方法；但通常更为常见的是描述性统计或推断性统计，描述性统计用以描述分数群组，推断性统计则可以仅用样本中包含的少量信息对分数总体进行估计；

社会科学中，”分数“常被用来描述人或发生在人身上的事件；

对实际或理论的分布的分数进行概率解释，是概率重要的原因；统计学家获取关于某些值分布的已知信息并将其表述为概率；

参考已知的值的分布信息，做出对值的概率解释；

划重点：表述概率方法的一个前提是，样本值必须从分布中随机抽取；

描述性统计：

统计学为描述一组分数所提供的解决方案；

推断性统计：

只有欲描述一组分数中的一部分（样本），但仍想描述整个组（总体）；

中心极限定理：

运用两个样本值和一个总体分数分布形态的假设，便可准确描述总体；

推断性统计用两个值来描述总体：平均数和标准差；

平均数：表现一组分数的趋中趋势（平均数中位数众数），这里用平均数，取所有分数的算数平均；平均数与群组中的各个分数的距离总和最小；
标准差：有关分数变异的信息，多数接近或远离平均数，最常用的变异度量概括了每个分数和平均数的距离；标准差就是这样一种变异度量，它是每个分数和平均数的平均距离（还可以用方差，它是标准差的平方）；

方差：在描述单一分布时并不是特别有用，但对比较不同分布的差异性很有帮助；方差常用作统计运算值，比如独立t检验；

# Tool 中心极限定理：
# - 如果你从总体中随机抽取多个样本，那么每一样本的平均数趋于正太分布；

衍生出来的数学规则：

这些平均数的平均数等于总体的平均数，凭借单样本的平均数，可对总体平均数做出很好的估计；
这些平均数的标准差等于（某一）样本标准差除以（该）样本量的平方根；
样本集合内的样本数量越大（>=30），上述结果越准确，分布也更接近于正太曲线；

中心极限定理的实际应用

给定一组样本值：[100, 95, 90, 92, 85, 88, 93, 91]
计算样本平均值：91.75
计算样本标准差：4.53，即该组样本中的大部分值在91.75的4.53左右；

要判断这组样本是不是从一个平均数是100的总体中随机抽取的，可以利用中心极限定理，从这组样本出发：

估计总体平均数：约为样本平均值91.75
估计总体标准差：约为样本标准差4.53
估计样本平均数在多大程度上偏离总体平均数
- 计算（多组采样）平均数的标准误差 = 样本标准差除以样本量平方根 = 4.53/(8)^(0.5) = 1.60；表示样本的平均数会在多大程度上偏离总体平均数；
- 即（多组）采样中的大多数样本平均值是在总体平均数的±1.60的范围内（划重点）；
- 因此，这组样本不是从一个平均数是100的总体中随机抽取的；

多组采样样本的平均值的平均值约为总体的平均值；

已经知道这些平均数是正太分布的，所以可以利用关于正态分布形态的知识，来生成一个精确的概率，如从平均数为100的总体中抽取平均数为91.75的样本的概率；

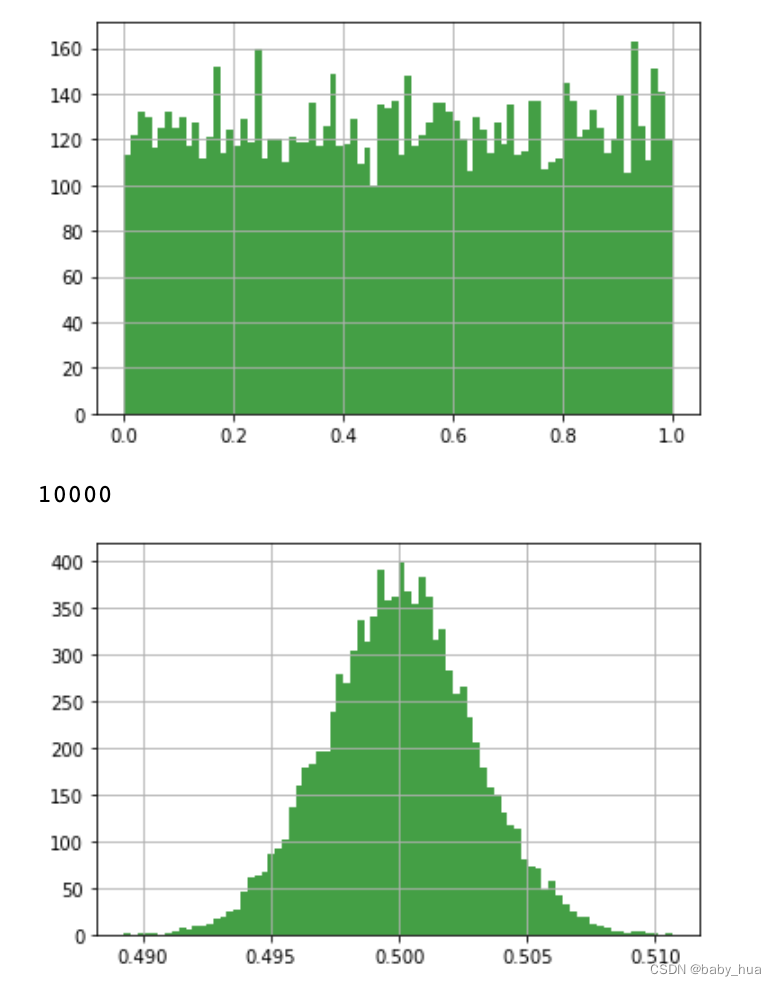
中心极限定理的一个模糊版本：受很多随机作用和无关事件影响的数据最终呈正态分布；可以应用正太分布特征对多数可见和不可见概念做概率解释；

中心极限定理的重要推论：

无论总体分布形态如何，从总体中随机抽取的（多组采样）平均数均呈正太分布；

独立筛子投掷概率表：

投掷得数	结果组合数	概率
2	1	0.028
3	2	0.056
4	3	0.083
5	4	0.111
6	5	0.139
7	6	0.167
8	5	0.139
9	4	0.111
10	3	0.083
11	2	0.056
12	1	0.028
总数	36	1

import numpy as np 
import matplotlib.pyplot as plt

if __name__ == "__main__":
#     一个验证中心极限定理的例子
    # 均匀分布
    u = np.random.uniform(0.0, 1.0, 10000)
    print(len(u))
    plt.hist(u, 80 , facecolor='g', alpha=0.75)
    plt.grid(True)
    plt.show()
    
    # 若干次叠加 取均值
    times = 10000
    for time in range(times):
        u += np.random.uniform(0.0, 1.0 , 10000)
    print(len(u))
    u /= times + 1
    plt.hist(u, 80 , facecolor='g', alpha=0.75)
    plt.grid(True)
    plt.show()

在这里插入图片描述

计算概率——概率定律

统计学的核心要点就是判断事件发生的可能性，计算概率的基本规则令统计学家有能力预测未来；

# Tool 概率定律：
# - 加法：几个互斥事件中任何一个发生的概率是各个事件发生的概率之和；
# - 相乘：一系列独立事件都发生的概率是每个独立事件概率的乘积；

概率中的主要原则就是用所关注的结果数除以全部结果的总数（概率基本公式=A/S）；

如经典的扔骰子问题，可以通过计算出两枚骰子点数之和等于期望数值的组合数量，来计算下次投掷时出现任何特定值的几率，除数是所有可能结果的总数；；

投出10/11/12任意一个就能赢的概率即三个独立的概率相加（0.083 + 0.056 + 0.028 = 0.167）；
连续3次投掷得10/11/12的概率即三个独立概率相乘（0.083 * 0.056 * 0.028 = 0.00013）

概率就是某事发生的可能性；

分析视角识别所有可能的结果并计算获胜结果所占结果的比例（即概率）；通过此概率来预测未来，预测准确性不太可能被检验；
相对频率视角：通过收集数据，观察实际发生了什么及其发生的频率来计算的；这实际是关于过去的解释，而不是对将来的预测；

否定虚无假设

科学的目标是构建一个解释世界的知识体系；假设检验是对科学的知识体系引进的新法则和理论，通过一系列逻辑步骤进行测试的过程；

一个假设是对可检验世界做出的一个估计；

验证假设是否合理可以收集数据、观察变量，测试变量间相关性：

数据支持假设，（是/否）支持假设，假设正确；
数据不支持假设，（是/否）抛弃假设，假设错误；

研究假设检验 所关注总体中变量X和变量Y之间存在相关性；（拥有的只是部分样本值的数据）

而统计假设检验，在假设检验结束时做出的概率解释，与研究假设为真的可能性无关；对研究假设为假的可能性做概率解释；更为准确的表达是“对于研究假设相反的假设为真的可能性做出解释”；这个相反的假设通常是关于变量间不存在相关性的假设，因此叫做虚无假设；

虚无假设检验 所关注总体中变量X和变量Y之间不具有相关性；

统计研究人员通过否定虚无假设就能证实他们的研究假设；

数据支持虚无假设，虚无假设正确/不正确，总体存在/不存在 相关性；
数据不支持虚无假设，虚无假设正确/不正确，总体 存在/不存在相关性；

数据不支持虚无假设，虚无假设错误，总体中存在相关性，这一结果支持了研究假设；

之所以检验虚无假设，是因为证明一个特定的估计不正确要比证实它正确容易得多；对于科学，可证伪的假设是最好的假设；

统计分析方式：

提出与研究假设相反的虚无假设；
然后尝试能否证伪该虚无假设；

许多现代统计学家认为应该集中精力对所关注的总体值（比如变量间相关性的大小）做出最佳估计，而不是证明相关性大小为某个不确定的非零值；

大数定律

减少样本误差的最佳方式是增加样本量（前提假设事件的发生或取样是随机的）；

预期值和观测结果之间的差距，称为标准误差；

样本结果的理论概率和实际发生概率之间的差距大小与以下的值成正比；

# Tool 大数定律的数学表示
# 1 / √(样本大小)

100个样本的误差大小仅为一个标准差的1/10，1000个时就已经相当准确了；

相比从总体中抽取少数人的样本，抽取多数人的样本更具有代表性；随着样本量增加，样本所体现的总体的重要特征越来越多，同时预测的准确性也随之提高；

大数定律为标准误差的计算提供了基础。

精确测量

一个良好的教育或心理学测试产生的分数是有效度和可信的；

效度（validity）是测试分数能在多大程度上体现你希望测量的特征，以及对测量意图的有用程度；

为了证明效度，必须提供证据和理论来支持测试分数的解释是正确的；

信度（reliability）是对同一个人多次重复测量得到相同测试分数的一致性程度；

要证明信度，需要收集重复测量的数据，并用统计学方法加以分析；

经典测试理论

信度理论（经典测试理论）方程式：观测分数 = 真分数 + 误差分数

观测分数：测试中取得的实际分数
真分数：指本该取得的分数，被定义为你无数次参加同一个测试，所得到的平均分数；这意味着真分数代表平均表现，一场测试也许会产生真分数，但未产生有效的分数；
误差分数：指你的观测分数与真分数的差距；随机误差可能会提高或降低分数；

我们知道信度是测试分数随机波动的程度，代表信度的数字通常通过观察测试中项目间的相关性来计算，这个指数范围分布在0.0和1.0之间，1.0表示一组没有任何随机误差的分数，指数越接近1.0，分数随机波动程度越小，信度越高。

标准误差的测量

尽管随机误差会在多次测试后达到平衡，但是不完美的信度依然有用，因为决策几乎总是基于单次测试分数所得；

在一个测试分数总体中，测量的标准误差是每个人的观测分数与其值分数之间的平均距离；

测量标准误差是利用测试的信度信息和群组观测分数的变异量（用标准差来反应）信息来估计的：标准误差 = 标准差 * √(1 - 信度)

示例说明：

某一测试分数范围200~800，均值500，标准差100；
该分数的估测信度通常在0.92左右；
你的单次测试得了520分，这是一个观测分数，它容易受随机误差影响；
那么，520有多接近你的真分数呢？

使用上面的 标准误差计算公式计算结果为 28，即本次的520分很可能处于多次所得平均分上下28分的区间内；

建立置信区间

观测分数很有可能在真分数的一个测量标准误差范围内；

68%置信区间：
- 观测分数落在真分数上下 一个标准误差 的区间内的
- （解释同：观测分数上下 一个标准误差的区间内是包含真分数的）
- 几率是 68%，即“很可能”；
95%置信区间：如果是95%的可能性使观测分数落在真分数上下的一个区间内，则这个区间需要在真分数上加减大约两个标准误差；

使用测量标准误差构建置信区间是基于：

误差（或误差分数）是随机的且呈正态分布；
由正态分布曲线能够计算精确的置信区间；

在正态曲线下，68%的值都在平均数的一个标准差之内，95%的分数都大约在两个标准差内（=1.96）；

测量标准误差是一个标准差，它是误差分数距真分数的标准差；

如果某次测量分数仍为520，95%置信区间就是464~576，即真分数的范围，那么就有95%的把握说，如果再考一次，新分数可能高达576分，或低至464分；

测量尺度

一共四种测量尺度：

名义测量
次序测量
等距测量
等比测量

不同尺度区别在于所含信息量，以及在何种程度上可对其进行有意义的数学和统计分析；

名义测量：用分数表示事务所属的不同类别；即把数字用做名称，作为表示不同类别的标签；如男1女2；

次序尺度：想用顺序或次序来分析掌握的分数；数值之间可比较，可排序；如成绩排名；次序测量提供了名义测量所提供的所有信息；

等距测量：任何两个毗邻的分数间有相等的差距，在次序尺度上增加了准确性这一元素；如温度，大多数教育和心里测量也都发生在等距测量这个尺度上；虽然等距测量看起来能解决所有问题，但是有一些数学运算在这个尺度上没有意义，例如温度80度降到40度，并不能说40度是80度的一半热；

等比测量，作为测量的最高尺度，提供了其他低尺度测量涵盖的所有信息，还能够进行比例比较和生成百分比；拥有绝对意义的零点（虽然有些变量没有绝对零点）；

在等距尺度，可以安全地进行描述性统计，执行推断统计分析，如t检验、方差分析以及相关性分析；

识别数据所使用的测量尺度，并利用该尺度的优势；自己生成的数据也可以考虑提高测量尺度，采用尽可能高的测量尺度；

如果你至少处于次序尺度，而且有把握能对等距尺度统计分析做出解释，那么你就可以在这种类型的数据上安全地执行推断性统计分析；

提高检验力

基于统计的研究，会遇到两种陷阱：

认定在总体中有发现，但这种发现其实只存在于他们手头的样本中；
样本中什么都没有，但总体中确实存在极秒的相关性，只是还没发现；

第一个问题可以通过代表取样而最小化，第二个可通过提升检验力来解决；

检验力

显著性检验：

判断样本中观测到的某个值有没有可能是随机发生的；
显著性只是意味着，关于样本的发现在总体中可能为真；
随机发生，则在总体中为假；不随机发生，总体中可能为真；

有显著性说明样本结果很可能不是偶然发生的；

显著性检验产生一个p值（概率值），表示样本可以从特定的相关总体中（随机）抽取的概率；

p值越低，可抽取概率越低，则可确定相关结果具有统计显著性；

通常，会将p值与余弦设定好的显著性水平进行比较，小于等于预先设定的值，就表明研究达到了一定的显著性水品；

统计检验的效力（即检验力）：指假定总体内的变量间存在相关性，统计分析达到显著性的概率；注意这是一个条件概率；

总体中必须存在相关性，否则，检验力毫无意义；

检验力公式组成：

样本量
预设要达到的显著性水平；
效应值（总体中相关性的大小）；

对这部分的理解，需要结合后续的内容；

执行检验力分析

假设要对比两组不同样本，看是否存在足够的差异，能够说明二者各自代表的总体检确实存在差异；

为了找到真正的差异，你要各调查采集多少样本？这就是一个检验力的问题：

你可以决定样本量
你可以选择，预设的显著性水平
你不知道的是，变量间相关性的实际大小（即效应值），这个需要从研究结果数据中得出；

效应值（所关注变量之间的相关性大小）可以被估计；检验力也可以被估计，通常研究人员会对最重要或最感兴趣的方面设定最小相关水平；

已知，样本量、显著性水平、效应值、检验力，其中的三个就可以求出第四个；

为了估计检验力，一个被普遍及接受的标准方法是：

将检验力目标值设为0.80；
将预设显著性水平设为0.05；

此时不同效应值所需样本量如下（具体推导很复杂，如在t检验中，效应值或者相关性大小指数，常用两组平均数差除以样本标准差所得的值来表达）：

效应值	样本量
0.10	1600
0.20	400
0.30	1750
0.40	100
0.50	65
1.0	20

效应值和样本量之间的关系是有意义的；这种普遍关系，反过来同样有效，在已知的效应值下估计，只需要提高样本量，到一定程度就会拥有你所需的检验力；

效应值越大，相关性越小，差异越大！

检验力水平在0.8，意味着总体中如果存在相关，那么研究人员就会有80%的几率在样本中发现相关性或效应；

推测极妙的相关性

检验力是当虚无假设为谬时，正确拒绝虚无假设的几率；几率越大，发现统计显著性的几率也越大；

检验力不等于成功的几率！它是在所有估计都正确的情况下，达到某个显著水平的几率；总体中的效应值是最难估计的；

展示因果

目标一：收集和分析有关世界的数据，用来支持或否定变量间关系的假设；
目标二：检验假设，看变量间是否存在因果相关；

两个因素相关，并不意味着二者之间存在因果；但如果两个变量不相关，似乎能排除一个变量是另外一个变量原因的可能性；

相关性存在使得英国关系有可能存在，但无法证明它的存在；

四种基本的实验设计类别，对应能否提供因果关系的强证据、中等证据、弱证据或无证据：

非实验设计：统计数据，描述或证明变量间相关性，不提供因果关系证明；
预实验设计：多套测量，穿插一些改变，观察变化，提供很弱的因果关系证明；
类实验设计：使用对照组（各组成员的分配不是随机的），能提供因果关系中等强度的证明；
实验设计：使用对照组（被试是随机分配到各组的，这可以使得研究人员假定所有的群组在未测量变量上是等同的），如果发现任何差异性，则把它们剔除作为备择解释；

四种实验设计类别可以组合嵌套使用；

如何检验”体重会影响身高“这一假设？

一个实验组和一个对照组，被试人员随机分配到组；
实验组，增加体重，观察身高是否变化
对照组，不对体重进行操控，测量身高是否发生改变；

这一实验中：

体重称作独立变量；
身高称作因变量（想知道它是否依赖于独立变量）；

这是实验符合实验设计的标准，但是否提供明确的因果关系证明，还需要考虑效度类型（带来的威胁）：

统计结论效度：变量间存在相关吗？
内部效度：该相关是因果相关吗？
构建效度：变量间的因果关系是否因此而受到影响？
外部效度：这因果关系到处都存在吗？

霍桑效应；

效应值

效应值这一统计工具，可以敏锐识别效应的大小，比如品牌A比品牌B好（“显著”结果），但究竟好多少，这个强度就可以用效应值来表达；

效应值是一个标准的值，表示两个变量间相关性的强度；

相关系数：提现两组分数关系强度和方向的指数;

发现或计算效应值

三种效应值的报告方式（都可被解读为对“变量间关系的大小”的估计）：

相关系数r：是对变量间关系的度量，是一种效应值；r可以是负的，有时也用r^2，解释为变量共享的“方差比例”；
d：归纳了t检验中所使用的两组平均数的差异；

# 计算方式1：通过两组平均数的差异 除以 两组平均标准差 而得到的；

# 计算方式2：

d = t * √((第1组样本大小 + 第2组样本大小) / (第1组样本大小 * 第2组样本大小))

η^{2：方差分析结果中报告的效应值的最常用表示，与r}2类似，被解释为因变量对独立变量贡献的“方差比例”；

判别效应值的参考标准：

效应值	小	中	大
r	±0.1	±0.3	±0.5
r^2	0.01	0.09	0.25
d	0.2	0.5	0.8
η^2	0.01	0.06	0.14

在讨论研究结果时，关注效应值的好处在于，能让每个人都大致了解，给定的研究变量对现实的实际影响有多大；

效用值搭配了显著性水品的研究报告，可以回答两个问题：

这种相关可能存在于总体中吗？
这种相关有多大？

如，两组患者，一组复用阿司匹林，另一组复用外观同的安慰剂，发现复用阿司匹林的患者患心脏病的几率是复用安慰剂的一半，这一发现在统计学上具有显著性；现在使用效应值进行解读：通过比较公式得到该研究的效应值d=0.06，与上表相比可知，该效应值非常小，这样的解读表明，服用阿司匹林和心脏病发作之间的确存在一个非常小的相关，相关性确实存在，只是不太强；