文章目录
- 位图(bitMap)
- 位图的实现
- 将数据添加到位图中
- 检查数据是否在位图中存在
- 将数据的对应位置置为0
- 位图的应用
- 布隆过滤器
- 为什么会有误差
- 布隆过滤器的实现
- 布隆过滤器的删除
- 使用Google下的guava组件操作布隆过滤器
- 布隆过滤器的缺陷
- 布隆过滤器的使用场景
- 海量数据的处理(位图&布隆过滤器的应用)
- 应用一
- 应用二
- 应用三
- 应用四
- 哈希的扩展应用
- 一致性哈希
- 哈希加密与加盐
位图(bitMap)
假如有一个文件(超过本身运行机器的最大内存),要求是快速地判断一个数是否在这个文件中存在。(假如一台电脑,运行内存是4G,在这个文件中存在40亿个不重复的无符号整数,那么必定超过4G内存的)请给出解决的方法。
对于这种情况,无论是直接遍历整个文件查找还是先对文件中的整数进行排序后利用二分查找都是不可取的,原因是使用这两种方案的前提需要先将数据加载到内存中才能执行的,但是很显然,内存肯定是存不下的(由题意)。
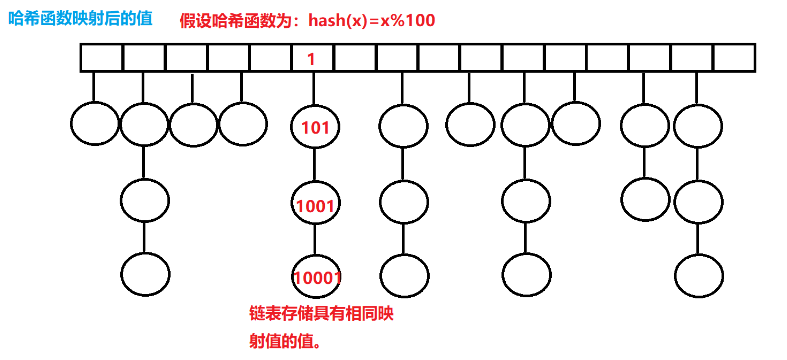
其实比较合理的方案是使用位图来实现,位图是将原本需要4字节(32bite)才能存储一个无符号整数压缩成1个bite为就代表1个无符号整数。在每一个bite位上只用0和1来代表整数的存在或者不存在,因此这些位上都是二进制比特位,经过这一通操作,就可以成功地将数据以原占用内存空间的1/32大小加载到内存中,于是就可以存得下了。之后判断一个数是否存在,则找到对应的下标判断位置上的二进制位是0还是1即可。
所以,位图就是用每一位来存放某种状态,适用于海量数据(数据无重复的整数)场景,并用来判断某个数据是否存在。
位图的实现
其实在Java中就内置了位图,在 util 包下的 BitSet 类就实现了位图,实际也是直接调用这个类即可。但是为了更进一步了解位图,下面会总结出模拟实现位图的代码(非源码)。
将数据添加到位图中
将数据添加到位图中,实际上就是将数据对应的比特位置为1。
具体步骤:需要先对准备插入的数进行验证,如果是小于0,则不符合要求;接下来就需要先确定这个数应该对应在哪一个字节上,其次再确定在哪一个比特位上,最后要将某一个比特位置为1,我们可以使用或运算来解决即可。要记得让usedSize加1。
public void set(int val){
if(val < 0){
throw new IndexOutOfBoundsException();
}
int arrayIndex = val / 8; //先确定在哪一个字节上
int bitIndex = val % 8; //确定在哪一个比特位上
this.elem[arrayIndex] |= (1 << bitIndex);
this.usedSize++;
}
检查数据是否在位图中存在
具体步骤:需要先对准备插入的数进行验证,如果是小于0,则不符合要求;接下来就需要先确定这个数应该对应在哪一个字节上,其次再确定在哪一个比特位上,最后判断对应比特位上是否是1,1则说明存在;反之不存在。
public boolean get(int val){
if(val < 0){
throw new IndexOutOfBoundsException();
}
int arrayIndex = val / 8; //先确定在哪一个字节上
int bitIndex = val % 8; //确定在哪一个比特位上
if((this.elem[arrayIndex] & (1 << bitIndex)) != 0){
return true;
}
return false;
}
将数据的对应位置置为0
具体步骤:需要先对准备插入的数进行验证,如果是小于0,则不符合要求;接下来就需要先确定这个数应该对应在哪一个字节上,其次再确定在哪一个比特位上,最后也是最重要的,不管原比特位上是0还是1,都需要变为0,所以我们需要先对1左移到对应的比特位上,按位取反再按位与后就可以将对应位置置为0。需要注意的是,我们最后需要将usedSize减1,但是也不能都减1,只有在原来比特位上是1的时候才能执行。
public void reSet(int val){
if(val < 0){
throw new IndexOutOfBoundsException();
}
int arrayIndex = val / 8; //先确定在哪一个字节上
int bitIndex = val % 8; //确定在哪一个比特位上
byte t = this.elem[arrayIndex];
this.elem[arrayIndex] &= ~(1 << bitIndex);
if(t != this.elem[arrayIndex]){
this.usedSize--;
}
}
位图的应用
在Java中BitSet的使用非常简单(调用几个函数来对数据进行插入、删除、查找)。除此之外,BitSet在对海量数据的处理中会经常看到,主要用于大数量的查找、去重、排序等工作,相比于其他的方法,占用的空间会更少,效率比较高。
拓展:BitSet也可以进行一些统计的工作(日志分析、用户数统计等),对集合进行运算(求并集、交集、补集等)。
布隆过滤器
如果我们需要经常判断一个元素(非整数)是否正确爱集合中存在,这时候就可以使用布隆过滤器,那么为什么是非整数呢?因为整数的话可以直接使用上面的位图解决。
在此之前,我们对这种操作一般是使用哈希表来解决,主要是哈希表的查找效率高。但是有一个问题,就是在海量数据的情况下,就需要考虑哈希表是否存得下了。比如说使用哈希表在存储大量名字,就需要将每一个字符串(名字)都存储起来,这时候在巨大的数据量下哈希表存储效率低的问题就显现出来了。
既然哈希表不能用来存储(原因:浪费空间),也不能使用位图(原因:只能存储整数),那么我们是否可以将两者结合起来,成为既能存储非整形又能压缩空间呢?答案是可以的,这就是下面要总结的布隆过滤器。
布隆过滤器是一种紧凑型的、巧妙的概率型数据结构,既有位图的高效插入和查询也有哈希表的多类型存储,它是使用多个哈希函数来将一个数据映射到位图中,不仅可以提升查询效率,也可以节省大量的内存空间。但是有一个缺点就是可能会出现误判的现象(只能判断某个数据一定不存在或者可能存在),可以无限减小误差,但是不能准确判断一定存在。
为什么会有误差
原因是每次将数据进行插入的时候,都是对这个数据调用不同的哈希函数生成整数,并分别存储到位图中,所以就可能会出现一种情况:一个字符串在位图中是不存在的,但是其通过哈希函数之后的整数在位图中对应的位置上都是1,那么这个时候布隆过滤器会误判其存在的。
当然,如果哈希函数尽可能多,那么误差就会趋近于无穷小,但是随之带来的就是效率的下降,因为哈希的次数变多了。另外,哈希函数的个数也需要权衡,个数越多则布隆过滤器 bit 位置位 1 的速度越快,且布隆过滤器的效率越低;但是如果太少的话,那我们的误报率会变高。
布隆过滤器的实现
其实在Java中谷歌已经给了组件guava可以直接实现布隆过滤器,实际开发也是这样子使用即可。但是为了更进一步了解布隆过滤器,下面会总结出模拟实现布隆过滤器的代码(非源码)。
class SimpleHash{
public int cap; //当前容量
public int seed; //随机
public SimpleHash(int cap, int seed){
this.cap = cap;
this.seed = seed;
}
//模拟HashMap实现哈希函数(根据seed的不同创建不同的哈希函数)
final int hash(String key) {
int h;
return (key == null) ? 0 : this.seed * (this.cap - 1) * ((h = key.hashCode()) ^ (h >>> 16));
}
}
public class MyBloomFilter {
public static final int DEFAULT_SIZE = 1 << 20;
private BitSet bitSet;
private int usedSize;
public static final int[] seeds = {5, 7, 11, 13, 27, 33};
public SimpleHash[] simpleHashes;
public MyBloomFilter(){
bitSet = new BitSet(DEFAULT_SIZE);
simpleHashes = new SimpleHash[seeds.length];
for(int i = 0; i < simpleHashes.length; i++){
simpleHashes[i] = new SimpleHash(DEFAULT_SIZE, seeds[i]);
}
}
//添加数据到布隆过滤器
public void add(String val){
//将不同seed下的哈希函数分别处理当前的数据,并存储在位图中
for(int i = 0; i < simpleHashes.length; i++){
bitSet.set(simpleHashes[i].hash(val));
}
this.usedSize++;
}
//判断是否包含val,会出现一定的误判
public boolean contains(String val){
//将不同seed下的哈希函数分别判断bitSet对应位置上是否为1
for(int i = 0; i < simpleHashes.length; i++){
if(!bitSet.get(simpleHashes[i].hash(val))){
return false;
}
}
return true;
}
}
布隆过滤器的删除
实际的布隆过滤器是不支持删除操作的,因为在删除一个元素的时候(简单地将比特位上的1置为0),就可能会影响到其他元素。
但是模拟实现的时候也可以将布隆过滤器中的每一个比特位扩展成一个小的数据(这样就可以支持删除操作),插入元素的时候给k个计数器(k个哈希幻术计算出的哈希地址)加1,这样子通过多占用几倍的存储空间的代价来增加删除操作,同时可能会出现计数回绕(溢出)的现象。因此,一般也都是不建议添加删除操作的。
使用Google下的guava组件操作布隆过滤器
当然,使用组件就需要创建Maven项目了。
第一步:在pom.xml文件中引入依赖:
<dependencies>
<dependency>
<groupId>com.google.guava</groupId>
<artifactId>guava</artifactId>
<version>19.0</version>
</dependency>
</dependencies>
第二步:新建一个测试类,编写下面这段代码:
public class Test {
private static int size = 1000000;//预计要插入多少数据
private static double fpp = 0.01;//期望的误判率
private static BloomFilter<Integer> bloomFilter = BloomFilter.create(Funnels.integerFunnel(), size, fpp);
public static void main(String[] args) {
//插入数据
for (int i = 0; i < 1000000; i++) {
bloomFilter.put(i);
}
int count = 0;
for (int i = 1000000; i < 2000000; i++) {
if (bloomFilter.mightContain(i)) {
count++;
System.out.println(i + "误判了");
}
}
System.out.println("总共的误判数:" + count);
}
}
由此,我们就可以调用guava下的布隆过滤器进行开发,我们在使用的时候直接规定误判率即可(不需要再循环调用哈希函数),非常的简便。
布隆过滤器的缺陷
- 会有一定的误判率(存在假阳性),不一定能准确判断元素是否在集合中。(但是同时可以建立一个白名单存储可能会误判的数据)
- 不能获取到元素本身。
- 不能对元素进行删除操作。
- 如果非要实现删除操作,以计数的方式可能会存在计数回绕的问题。
布隆过滤器的使用场景
- 使用爬虫爬取网页数据,使用布隆过滤器可以高效对url进行去重,避免爬取相同的url地址。
- 垃圾邮箱的过滤,在上百亿个垃圾邮件中判断某一个邮箱是否是垃圾邮箱。
- 在秒杀系统中,快速查看用户是否重复购买。
- ……
海量数据的处理(位图&布隆过滤器的应用)
应用一
给一个超过100G大小的文件,文件中存储着大量的IP地址,请找出最多的IP地址以及topK的IP地址。
我们可以使用哈希切割的方法,来将相同的IP存储到同一个文件中,具体的操作步骤是:1.先将IP地址通过哈希函数转化成一个整数;2.对哈希之后的数对200取模(不一定非要是200,符合条件即可),存储到不同的文件中,这样就可以把相同的字符串映射到同一个文件中;3.分别读取每一个文件中的内容,统计每一个文件中IP出现的次数即可解决此问题。
通过这样的操作,不仅能找到最大的,使用排序或者是优先级队列也就可以很容易找出topK了。
应用二
给出超过100亿个整数,请找出只出现一次的整数。
对于这个问题,具体有3种解法。
第一种:使用切割的思想(与上面一样)。将这些整数分到不同的文件中,之后遍历每一个小文件,统计数字出现的次数。
第二种:使用两个位图进行判断。对没出现过的数两个位图上的对应位置都是0;对只出现一次的数,位图1对应位置保持0不变,位图2对应位置置为1;对出现两次的数,位图1对应位置置为1,位图2对应位置重新置为0;对出现过三次及以上的,两个位图对应位置都保持1不变。
第三种:使用一个位图进行判断。原本我们的位图是一个比特位存一个数,但是这种方法需要我们重新改造这个位图,变成两个比特位存一个数,一个比特位是用来判断树是否存在,另一个比特位是用来判断这个数出现的次数(0代表只出现1次,1代表出现2次及以上)。
应用三
给出两个文件,分别都有超过100亿个整数,请找出两个文件中的交集。
对于这个问题,具体有2种解法。
第一种:使用切割的思想。先遍历第一个文件,将第一个文件中的数据存到bitSet中,再遍历第二个文件,边遍历边看这个数据是否在bitSet中存在,存在的话,那么这部分就是交集。
第一种:使用两个位图进行判断(不仅可以判断交集,还可以判断并集和差集)。将两个文件的数据分别存到两个位图中(保证两个位图大小相等),将这两个位图按位与就可以得到交集;将两个位图按位或就可以得到并集;将两个位图安慰异或,就可以得到差集。
应用四
给出两个文件,分别都有超过100亿个query,请找出两个文件中的交集(给出精确以及近似的做法)。
精确的做法其实就是哈希切割的思想解决即可。
近似的做法其实就是使用布隆过滤器。先遍历第一个文件,将query插入到布隆过滤器中,再遍历第二个文件,在布隆过滤器中查找即可得到交集(存在误判)。
哈希的扩展应用
一致性哈希
在总结一致性哈希之前,需要先了解分布式存储。分布式存储就是把存储的数据分布到不同的服务器上,这样子的好处就是把数据分流在不同的服务器上,避免大量的数据涌入同一台服务器而导致雪崩的现象。
通常来说,分布式存储都是结合哈希的,但是如果单单只是采用和 hashmap 实现一样的思路,通过和实体机的数量取模自然映射到不同的机器显然是不可取的,原因是如果其中一台机子挂了,或者又加了一台机子的情况下,会导致挂了的数据将无法得到恢复,新增的机子也无法得到利用的情况,更严重的可能会其他服务器面临崩溃的风险。
这时候就需要一致性哈希了。我们假设有一个环,叫做“哈希环”,是由2^32个点组成的。我们可以使用 hash(key) % 2^32 来表示服务器在哈希环的位置,然后要把数据存储到服务器中的时候就需要先将数据 hash(val) % 2^32 存储到哈希环上,之后指定一套规则,将数据按顺时针的方向寻找,直到找到服务器并存储进去。这样子使用环的结构就不会出现其中一台机子挂了,或者又加了一台机子而导致服务器崩溃的情况了。
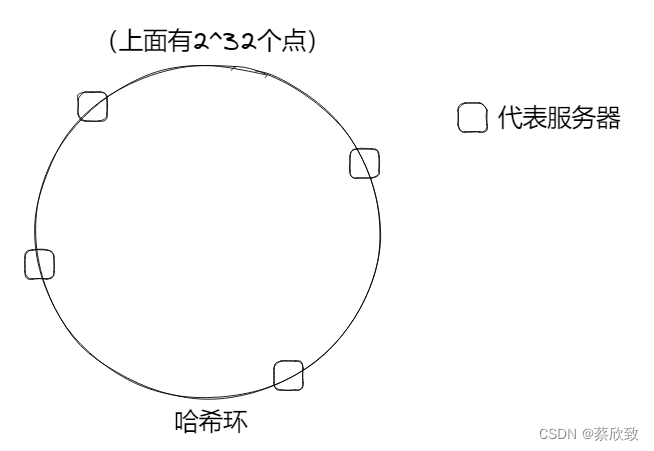
但是仔细观察过后,仅仅只是上面这个模型还会存在一些问题:如果服务器在这个环上的分布是比较集中的(非均匀分布),这时候就会导致其中部分服务器的压力比较大,而部分服务器几乎没什么存储的情况。当其中一台服务器出现宕机(负载不均衡)的话,可能就会导致一连串的服务器出现崩溃。
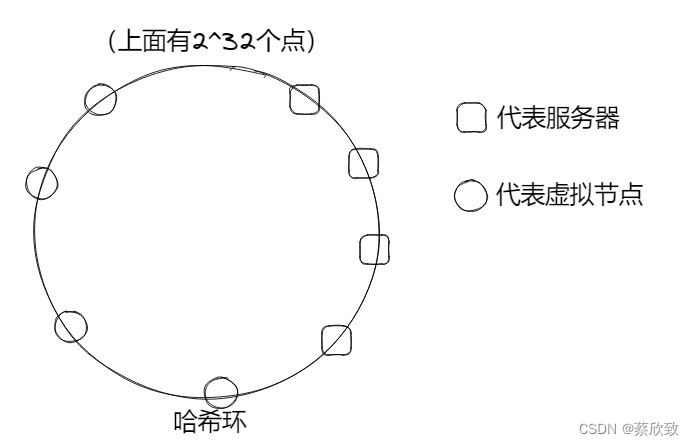
解决这一情况的方法是使用虚拟节点。虚拟节点是实际节点在 hash 空间的复制品(如图),这样就可以是数据哈希的结果能够尽可能分布到所有的缓冲中(服务器+虚拟节点)去,可以使得所有的缓冲空间都得到利用,进一步保证了平衡性。
哈希加密与加盐
对于哈希的加密,这部分知识会在后面博客中详细总结,因为这是与很多项目都相关的(打算放在项目博客的地方比较好),相关的比如用户的登录,需要对用户输入的密码进行加密的操作。
这里简单做个介绍:普通的加密是使用MD5进行加密,MD5加密是用哈希函数产生的一串密文,虽然这是不可逆的,但是这样的操作安全级别也是比较低的,因为对于同一个密码无论怎么哈希,结果都是不会变的,这时候就可以提前准备好一个“彩虹表”,通过你的这一段密文在表中暴力查找,也是可以反推出密码的。在目前的开发中,比较常用的还是加盐加密,由于加盐加的是随机盐,也就是在原本的密码基础上随机加上一串字符,再进行哈希,这样就可以实现每次生成的密文都是不一样的,同时由于对方无法直到你拼接的字符串的规则,也就很难推出原本的密码了,大大提高了安全性。当然这也不是完全就破解不了,只是增加了破解的成本,要知道任何密码都不是绝对安全的。